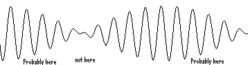ميكانيكا الكم
| جزء من سلسلة مقالات عن |
| ميكانيكا الكم |
|---|
ميكانيكا الكم Quantum mechanics نظريّة فيزيائية أساسية ، جاءت كتعميم وتصحيح لنظريات نيوتن الكلاسيكية في الميكانيكا. وخاصة على المستوى الذري ودون الذري . تسميتها بميكانيكا الكم يعود إلى أهميّة الكم في بنائها(وهو مصطلح فيزيائي يستخدم لوصف أصغر كمّية يمكن تقسيم الإشياء إليها ، ويستخدم في للإشارة إلى كميات الطاقة المحددة التي تنبعث بشكل متقطع ، وليس بشكل مستمر). كثيرا ما يستخدم مصطلحي فيزياء الكم والنظرية الكمومية كمرادفات لميكانيكا الكم. وبعض الكتّاب يستخدمون مصطلح ميكانيكا الكم للإشارة إلى ميكانيكا الكم غير النسبية.
التاريخ
| الفيزياء الحديثة |
|---|
| |
 مقالة مفصلة: تاريخ ميكانيكا الكم
مقالة مفصلة: تاريخ ميكانيكا الكم
أتت النظرية الكمومية (و تسمى ايضا النظرية الكوانتية quantum theory )في بدايات القرن العشرين مثل النظرية النسبية لحل اشكاليات مطروحة من قبل النظرية الكلاسيكية ، و يمكن تلخيص هذه الاشكاليات بعدم التناسق بين درجات حرية الجسيمات (6) و درجات حرية الحقول (عدد غير محدود ) فحسب قانون توزع الطاقة بالتساوي بين مختلف درجات حرية الجملة في حالة التوازن ، الذي يؤدي إلى انتقال معظم الطاقة من الجسيمات إلى الحقول ، و ينتج عن هذا تصورات مخيفة مخالفة للواقع : فحسب هذه النظرة يجب على الالكترون الدائر حول النواة ( حسب نموذج رذرفورد ) أن يصدر أمواجا كهرومغناطيسية وفقا لمعادلات مكسويل تزداد شدتها إلى اللانهاية، و بهذا يقترب أكثر فأكثر من النواة حتى تنهار جميع الالكترونات ضمن النواة، لكن من المؤكد أن هذا لا يحصل في الواقع . تقول النظرية الكلاسيكية أيضا أن اصدارات الذرة الضوئية يجب أن تغطي جميع الترددات بنفس الشدة ، لكن الواقع ينقض ذلك بشدة حيث تبدي الذرات المختلفة أطيافا خاصة تتضمن اصدار امواج ضوئية على ترددات خاصة و محددة جدا .
تنشأ مشكلة أخرى عندما نتأمل اشكالية الجسم الأسود "وهو جسم يمتص كامل الاشعاع الساقط عليه ليعيد اصداره" حيث فشلت كل المحاولات المستندة إلى الميكانيك الإحصائي الكلاسيكي في توصيف اشعاع الجسم الأسود خصوصا في الترددات العالية حيث تبدي القوانين المتوقعة انحرافا كبيرا عن الواقع و هذا ما عرف لاحقا باسم الكارثة فوق البنفسجية .
أتت بدايات الحل في عام 1900 مع ماكس پلانك الذي اقترح فكرة ثورية هدفها التنبؤ بتناقص الأنماط العالية التردد من اشعاع الجسم الأسود بافتراض ان الاهتزازات الكهرطيسية تصدر بشكل كموم ، حيث يعتبر الكم أصغر مقدار معين من الطاقة يمكن تبادله بين الأجسام وفق تردد معين ، و ترتبط طاقة الكم بتواتر الاشعاع المرافق له :
حيث تعبر عن طاقة الكم الصادر ، عن تواتر الاشعاع\تردده ، ثابت أصبح يدعى بثابت بلانك .
تأتي اشكاليات أخرى من التبصر في طبيعة الضوء ففي حين يؤكد نيوتن ان طبيعة الضوء جسيمية ( فهو مؤلف من جسيمات صغيرة، و تؤيده في ذلك العديد من التجارب ، نجد أن يونغ يؤكد أن الضوء ذو طبيعة موجية و تؤكد تجارب يونغ حول التداخل الضوئي و الانعراج هذه الطبيعة الموجية . في عام 1923 اقترح لويس دو بروي أن ينظر إلى جسيمات المادة و ذراتها أيضا على انها جسيمات تسلك سلوكا موجيا احيانا مقترحا معادلة تشابه معادلة بلانك :
.
حيث : λ, طول الموجة ، و p العزم.
بدأت هنا تتضح ملامح صورة جديدة للعالم تتداخل فيها الجسيمات و الحقول المهتزة بحيث يصعب التمييز بينهما و كان هذا ما مهد الطريق لظهور ميكانيك الكم عندما وضع نيلز بور نظريته الذرية التي لاتسمح للاندفاع الزاوي بأخذ قيم سوى المضاعفات الصحيحة للقيمة :
حيث تعبر عن قيم الاندفاع الزاوي ، عدد صحيح (3,2,1,...)
و هكذا ظهرت مستويات للطاقة المستقرة يمكن وضع الالكترونات الدائرة فيها مفسرة ثبات التركيب و الخطوط الطيفية للذرات ، لكن هذا لم يكن سوى البداية . في عام 1925 قام العالم الالماني هايزنبرگ بتقديم مبدأه في الارتياب الذي ينص على عدم قدرتنا على تحديد موضع و سرعة ( اندفاع ) الجسيمات الكمومية بآن واحد و بدقة متناهية . كانت هذه بداية سلسلة من الصدمات التي تلقتها نظرتنا الكلاسيكية للعالم و التي تحطمت معها كل الصورة الميكانيكية الآلية التي سادت حول العالم بعد انتصارات فيزياء نيوتن المدوية في القرنين السابقين . قام هايزنبرگ بصياغة قواعد ميكانيك الكم بصياغة جبر المصفوفات فيما عرف بعد ذلك بميكانيك المصفوفات matrix mechanics ، 1926 ظهر شرودنگر بمعادلته الموجية الشهيرة التي تبين تطور دالة موجة الجسيم الكمومي مع الزمن و عرفت تلك الصياغة بميكانيكا الموجات wave mechanics ، لكن رغم الاختلاف الظاهري العميق بين الصياغتين فان نتائجهما كانت متطابقة ، هذا ما دفع پول ديراك بعد ذلك لتوحيدهما في اطار شامل عرف بنظرية التحويل transformation theory.
تركيبات رياضية
 مقالة مفصلة: تركيبات رياضية لميكانيكا الكم
مقالة مفصلة: تركيبات رياضية لميكانيكا الكم

تركيبات رياضية تعادل ميكانيكا الكم
التفاعل مع النظريات العلمية الأخرى
ميكانيكا الكم والفيزياء الكلاسيكية
النسبية وميكانيكا الكم
Attempts at a unified field theory
 مقالة مفصلة: Grand unified theory
مقالة مفصلة: Grand unified theory
الآثار الفلسفية
 مقالة مفصلة: تفسيرات ميكانيكا الكم
مقالة مفصلة: تفسيرات ميكانيكا الكم
التطبيقات
أمثلة
الجسيمات الحرة
Step potential
Rectangular potential barrier
 مقالة مفصلة: Rectangular potential barrier
مقالة مفصلة: Rectangular potential barrier
جسيمات في صندوق
 مقالة مفصلة: جسيمات في صندوق
مقالة مفصلة: جسيمات في صندوق
Finite potential well
 مقالة مفصلة: Finite potential well
مقالة مفصلة: Finite potential well
مذبذب متناسق
 مقالة مفصلة: مذبذب متناسق الكم
مقالة مفصلة: مذبذب متناسق الكم
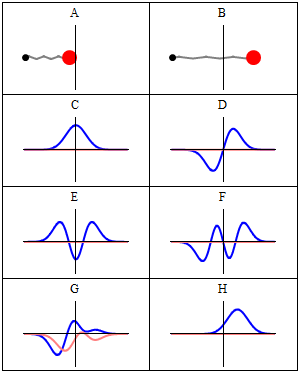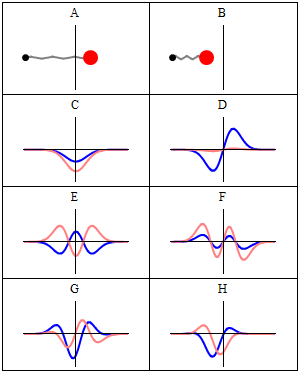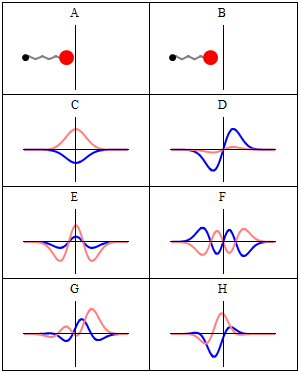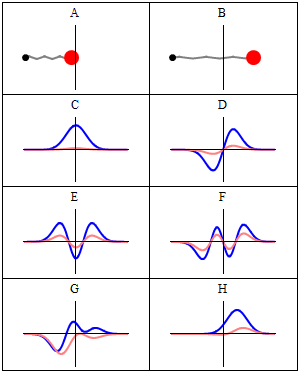
نموذج بور للذرة
اقرأ المقال الرئيسي : نموذج بور
أظهرت تجارب راذرفورد أن الذرة تتكون من مركز مشحون إيجابا يسمى نواة وإلكترونات تتحرك حولها. بينت أعمال علماء الذرة حول أطياف الإمتصاص و الإنبعاث أن هذه الأطياف متقطعة وليست مستمرة. هذه الخاصية وجدت تفسيرها الأول فيما يعرف بنموذج بور للذرة. كانت أهم فرضية لبور هي أن الإلكترونات لا يمكنها سوى الحركة في مدارات دائرية يكون فيها الإلكترون مستقر أي لا يشع و إلا فإنه بعد مرور فترة من الزمن سوف يفقد كل طاقته و يسقط على النواة. هذا يعني أن الإلكترون لا يمكنه أن يحتل إلا سويات طاقة معينة أي أن طاقته مكممة. في حالة أستثارة الذرة فإن الإلكترون سوف ينتقل إلى سوية طاقة أعلى ثم يعود إلى حالته الأولى مع انبعاث فوتون ذو طاقة مساوية تماماللفرق بين طاقتي السويتين .
النظرية الكمومية حسب التصور الموجي
لا تقوم صياغات الميكانيك الكمومي بتقديم قياسات دقيقة لخواص الجسيمات المقيسة observables بل تعطي تنبؤات أي توزعات احتمالية probability distributions لجميع القيم التي يمكن أن تأخذها خاصة معينة للجسيم ، فالحالة الكمومية للجسيم تتضمن احتمالات لخواصه القابلة للقياس : مثل الموضع Position ، العزم Momentum ، الطاقة Energy ، العزم الزاوي angular Momentum . هذه الخواص يمكن أن تشكل بقيمها توابع مستمرة continuous مثل الموضع و يمكن ان تشكل توابع منقطعة discreteمثل الطاقة .
بهذا لا يعطيك ميكانيك الكم الموقع الدقيق لجسيم انما يعطيك احتمال وجوده في أي نقطة من الفضاء حيث يحدد مسارات يكون فيها تواجد الجسيم أعظميا( اي احتماليته اعظم من غيره) لكنه لا يلغي امكانية وجوده في أي نقطة من الفراغ و يمكنك قول نفس الكلام بخصوص جميع الخواص الأخرى .
لكن تبقى هناك حالات معينة تتضمن تحديد قيم دقيقة لبعض الخواص, تدعى هذه الحالات بالحالات الخاصة Eigenstates.
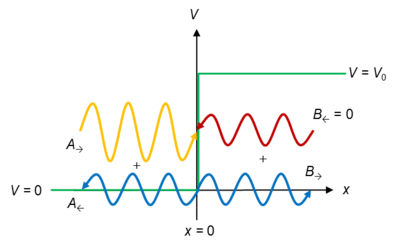
لنفترض وجود جسيم غير مقيد حر الحركة ، مما يعني امكانية تمثيل حالته الكمومية بموجة ذات شكل افتراضي غير معين و تمتد على كامل الفضاء ندعوها بدالة الموجة . قياسات الجسم في هذه الحالة تتضمن موضعه و عزمه . فلو أخذت دالة الموجة سعة عالية جدا في موضع (س) و كانت قيمها معدومة ( صفر ) في كل الأماكن الاخرى فهذا يعتبر حالة خاصة للموضع : يتحدد بها موقع الجسيم بدقة. في الوقت ذاته يجب ألا ننسى أن هذا يتضمن عدم القدرة اطلاقا على تحديد قيمة العزم حسب مبدأ الارتياب . لكن في الحقيقة لا توجد مثل هذه الحالات الخاصة للخواص المقيسة لكن تدخلنا بعملية قياس أي من الخواص يحول تابع موجته من شكلها الأصلي إلى حالة خاصة لهذه الخاصة و هذا ما يدعى بانهيار الموجة wave collapse.
لنفترض جسيما كموميا وحيدا : من وجهة نظر كلاسيكية يلزمنا تحديد موضع و سرعة الجسيم أما النظرية الكمومية بالصياغة الموجية لشرودنغر قتعتبر ألا وجود لمثل هذا الخواص المقيسة مثل : الموضع ، العزم ، الطاقة فكل موضع متاح للجسيم هو موقع محتمل و كل قيمة متاحة للطاقة هي قيمة ممكنة أيضا ، و الاختلافات بين قيمة و أخرى هي اختلافات في الاحتمالات. حيث يكون لهذه الدالة في كل موقع(س) قيمة معينة () تدعى سعة وجود الجسيم في الموضع (س) ، فيكون احتمال وجود الجسيم في الموقع (س) هو ببساطة مربع سعة وجود الجسيم في الموقع (س) . اما عن حالات اندفاع الجسيم فسنضطر هنا إلى اجراء تحليل توافقي لدالة الموجة و مجموعة توافقيات هذه الموجة يمثل الحالات الممكنة لاندفاعات الجسيم و بهذا نحصل على دالة موجية للاندفاع ضمن فضاء افتراضي للاندفاعات تكون غالبا بشكل أمواج اما شديد التراص مما يدل على حالة شديدة الاندفاع أو قليل التراص و هذا يمثل حالات قليلة الاندفاع .
تقوم معادلة شرودنغر بوصف تطور دالة الموجة مع الزمن و بهذافهي تقوم بالتنبؤ الدقيق للحالات الكمومية للجسيم في أي لحظة و بهذا تقدم لنا قانونا ثابتا يشرح تطور الدالات الموجية بكل دقة ، هذه الدالات التي تكون في داخلها جميع قيم الموضع و الاندفاع المحتملة . فدالة الموجة التابعة للجسيم حر الحركة تتنبأ بان مركز الحزمة الموجية سيتحرك مع الزمن بسرعة ثابتة و بنفس الوقت سيزداد امتداد الموجة ليصبح الموضع أكثر فأكثر غير محدد . توجد أيضا بعض الجمل الكمومية المستقرة التي لا تبدي تغيرا مع الزمن كحالة الالكترون في ذرة الهيدروجين و الذي يصور في ميكانيك الكم كموجة احتمالية مستقرة دائرية : يكون تواجد الالكترون أعظميا ضمن بعد معين من النواة في حين يقل الاحتمال تدريجيا كلما ابتعدنا عن النواة . تطرح معادلة شرودنغر اذن تطورا حتميا للدالة الموجية (يدعى هذا التطور بالتطورU ) فهي تحدد بدقة قيم الدالة في جميع نقاط الفضاء في أي لحظة زمنية ، لكن الطبيعة الاحتمالية لميكانيك الكم ينشأ من التدخل بعملية القياس لتحديد احدى الخواص المقيسة للجسيم عندئذ يحصل التطور R اللااحتمالي تأخذ بموجبه الخاصة المقيسة أيا من القيم المتاحة لها حسب قيمة احتمالها و هذا ما يكافئ ما دعوناه مسبقا ب ( انهيار الدالة الموجية ) .
نتائج النظرية
تكميم الخواص الفيزيائية
مثنوية (جسيم/موجة)و مبدأ الارتياب
لا يعطينا ميكانيك الكم تنبؤا دقيقا بنتيجة رصد أو قياس جملة كمومية أو جسيم كمومي انما يكتفي باعطاء محموعة من النتائج الممكنة و المختلفة لكل منها احتمال وجود معين . كما لا يستطيع تحديد طبيعة الجسيم ان كانت جسيمية أو موجية فهو يعتبر هذه الطبيعة نتيجة الرصد و القياس فعندما توجه اهتمامك للخاصية الموجية للجملة ترصد تلك الخواص و عندما تهتم بالخواص الجسيمية تبدو الجملة بشكل جسيم .
أول ما ظهرت هذه المثنوية ( جسيم / موجة ) في تجربة يونغ الضوئية الشهيرة ، فاستخدام ثقب واحد لمرور الضوء كان يؤكد الخاصية الجسيمية ( التي تجلت فيما بعد بما دعي الفوتون ) في حين كان فتح ثقبين يؤدي لظهور مناطق التداخل المضيئة و المظلمة . انعراج الضوء كان دليلا واضحا ايضا على طبيعة الضوء الموجية في حين أكدت أطياف الذرات و تفسير ماكس بلانك لها بأن الضوء عبارة عن طاقة تصدر بشكل كميات متقطعة متجانسة تدعى الكموم ( و تمثلت تلك الكموم بالفوتونات في تجربة المفعول الكهرضوئي ) الطبيعة الجسيمية للضوء.
اتت بعد ذلك علاقة دوبروي و مبدأ الارتياب Uncertainity principle لهايزنبرغ ليمددا هذا التصور المثنوي باتجاه جميع الجسيمات الذرية atomic particles و تحت الذرية sub-atomic ، و اصبح من الممكن الحديث عن تداخل الاجسام كما الحديث عن تداخل الأمواج ، فقد أجريت تجربة مشابهة تماما لتجربة يونغ استخدم بها الالكترونات بدلا من الفوتونات الضوئية و حصلنا بالمقابل على مناطق ذات شدة الكترونية و مناطق محرمة على الالكترونات و هذا عزز التأكيد أن الالكترونات كما الفوتونات تتصرف كموجة وجسيم معا . و اذا اعتمدنا تفسير كوبنهاجن لميكانيك الكم فان كل الجمل الكمومية ليست لا موجة و لا جسيم انما دالة موجية wave function تعبر عن نفسها كموجة wave أو جسيم particle حسب توجه عملية الرصد البشري و القياس .
مبدأ الارتياب في الطاقة والزمن
لا يقتصر دور مبدأ الارتياب لهايزنبرغ على تقييد مقدار الدقة certainty الممكنة في تحديد الموضع Position و الاندفاع بل يتعداه إلى كافة الخواص الفيزيائية كالطاقة Energy و الزمن Time; فطاقة الفوتون مثلا تتحدد بتحديد تواتر frequency أمواج الضوء لكن تحديد هذا التواتر يتطلب عد الاهتزازات في فترات زمنية من مضاعفات زمن اهتزاز الموجة ، الذي يمثل أصغر فترة زمنية لانجاز اهتزاز ضوئي وحيد . بالتالي هناك حدود لقياس الزمن مطلوبة لتحديد التواتر و استخدام فترات زمنية أصغر من زمن اهتزاز الموجة الضوئية يجعل طاقة الفوتون غير محددة ، مما ينشيء علاقة ارتياب جديدة بين الطاقة و الزمن . تتجلى هذه العلاقة الارتيابية في ظاهرة الأطياف فاحداث تهييج قصير المدة لمجموعة متماثلة من الذرات يؤدي إلى نقل بعض الالكترونات إلى سويات طاقية أعلى لكن غير محددة ( بسبب قصر الفترة الزمنية ) بالتالي نحصل على طيف ضوئي متنوع الأمواج ( يغطي المجالات الضوئية السبع و فوق البنفسجية و تحت الحمراء ) ، بالمقابل عندما نقوم بعملية تهييج ذرات لقترات زمنية طويلة تسمح بكون السويات الطاقية energy levels للالكترونات المهيجة excited electrons محددة, و بالتالي نحصل على طيف spectrum ذو خطوط موجية معينة تعكس البنية المدارية للذرات.
مثل هذا الاستنتاج قد يعمل على تعطيل قانون حفظ الطاقة في فترات زمنية قصيرة جدا ، بصياغة اخرى يمكن للجملة الكمومية الحصول على قرض طاقي بشرط ان تعيده خلال مدة زمنية قصيرة جدا ، تتحدد مدة القرض الطاقي بكمية الطاقة فكلما ازداد مقدار الطاقة وجبت اعادتها في زمن أقل : ينتج عن هذا ععدد من النتائج المهمة مثل : ( تبعثر الضوء بفعل الذرات ، مفعول النفق و هو عملية اجتياز بعض الجمل الكمومية لحواجز طاقية مرتفعة عن طريق قروض طاقية : يفسر مفعول النفق قدرة العديد من الجسيمات الكمومية على اجتياز بعض الحواجز الطاقية رغم عدم امتلاكها للطاقة اللازمة بنسب احتمالية ، و يدخل هذا في تفسير ظاهرة العناصر المشعة .
صياغة ديراك لميكانيك الكم
قام بول ديراك بوضع ميكانيك الكم بصيغتيه : ميكانيك المصفوفات Matrix Mechanics و الميكانيك الموجي Wave Mechanics ضمن صياغة أشمل جمعها بنظرية النسبية الخاصة و هذا ما أدى إلى عدد من النتائج الجوهرية أولها :
- ادخال خاصية دوران الأجسام الذرية حول نفسها Spin : فالالكترون يدور حول النواة كما يدور حول نفسه و هذه الخاصة دعيت ب ( السبين spin ) . كما اسند للسبين قيمة عددية تشرح خاصيات الدوران الجسيمي :
- تنبأت نظرية ديراك بسويات طاقية ضمن الذرة غير مكتشفة بعد ، فلكل حل يصف الكترونا في سوية طاقية يوجد حل نظير تماما ( كخبال المرآة ) يماثله في الخواص و الطاقة لكن طاقته سالبة ، وجود مثل هذا الجسيم يمكن أن يؤدي في حالات معينة لظهور اجسام شبيهة بالالكترونات ذات شحنة موجبة و طاقة موجبة دعيت بالبوزيترون : و قد ثبت ظهور هذه البوزيترونات في بعض التفاعلات النووية . و كان هذا بداية اكتشاف المادة المضادة التي تنشأ عن جسيمات الطاقة السالبة .
- نتج مبدأ الانتفاء لباولي عندما كان يدرس اجتماع الجسيمات ذات السبين : حيث بين انه لا يمكن لجسيمين كموميين أن يحتلا نفس السوية الطاقية ، فحتى الالكترونين المحتلين لمدار (سوية طاقية) واحد ضمن الذرة يجب أن يكون احدهما ذو سبين +2/1 و الآخر -2/1 و بهذا تكون حالتهما الكمومية مختلفة.
تفسيرات النظرية الكمومية
تقوم النظرية الكمومية بتقديم تصور غريب عن العالم الذري و دون الذري يصدمنا و يبعدنا عن كل ما الفناه في الواقع الحياتي و ما تقدمه الفيزياء الكلاسيكية من تصورات . لكنها بالرغم من كل ذلك تنجح إلى حد بعيد في تفسير حقائق العالم دون الذري و تعزز صحتها يوما بعد يوم بتقديم تنبؤات غريبة لكن كل التجارب العلمية تأتي فيما بعد لتؤكد هذه التنبؤات . كل هذا أدخل ميكانيكا الكم في عمق نقاشات فلسفية حول طبيعة ما تطرحه و مدى قربه من الحقيقة ، حتى أن ميكانيكا الكم طرحت نفس قضية الحقيقة كموضع سؤال ، ومن أهم هذه المناقشات و التجارب الفكرية : قطة شرودنغر و صديق فاغنر .
لقد قدمت عدة وجهات نظر لتفسير نتائج و استنتاجات النظرية الكمومية : أول هذه النظريات يعرف بتفسير كوبنهاجن و يعود بشكل أساسي إلى بور و زملائه ، الذين يؤكدون أن الطبيعة الاحتمالية probabilistic لتنبؤات نظرية الكم لا يمكن تفسيرها بأي نظرية حتمية deterministic أخرى ، و هي صفة أصيلة في الطبيعة التي نعيش بها و ليست نتاجا لنقص في المعرفة و المعلومات نعاني منه . باختصار النظرية الكمومية ذات طبيعة احتمالية لأن الطبيعة ذات طبيعة احتمالية اساسا فما تفعله النظرية الكمومية هو تصوير الأمر كما هو .
على الطرف الآخر وقف اينشتاين أحد مؤسسي الكمومية ليعلن رفضه للاحتمية الكمومية التي تنشأعن احتمالية القياسات ، قائلا ( ان الاله لا يلعب النرد God doesn’t play dice ) . كانت هذه العبارة الشهيرة بمثابة رفض قاطع لفكرة ان تكون للطبيعة أصالة احتمالية ، مرجحا فكرة ان هناك نقص في المعلومات المتوفرة لدينا يؤدي إلى تلك الطبيعة الاحتمالية للنتائج وعليه فنظرية الكم ناقصة ينبغي اكمالها عن طريق تعويض النقص بالمعلومات و هو ما دعاه بالمتغيرات الخفية hidden variables فعن طريق هذه المتغيرات يمكن صياغة نظرية كاملة ذات طبيعة حتمية .
ظهرت بعد ذلك بعض التفسيرات التي تضاهي بغرابتها نتائج و نبؤات الكمومية مثل نظرية العوالم المتعددة لايفريت ، حيث تقول هذه النظرية بأن جميع الاحتمالات التي تطرحها نظرية الكم تحصل فعليا بنفس الوقت في عدد من العوالم المستقلة المتوازية . و بالتالي يكون الكون المتشعب حتميا في حين أن كل كون فرعي لن يكون الا احتماليا .
هناك ايضا تفسير لبوم يعود إلى ديفيد بوم و يفترض وجود دالة موجية عالمية غير محلية تسمح للجزيئات البعيدة بأن تتفاعل مع بعضها بشكل فوري . اعتمادا على هذا التفسير يحاول بوم أن يؤكد أن الواقع الفيزيائي ليس مجموعة من الجسيمات المنفصلة المتفاعلة مع بعضها كما يظهر لنا بل هو كل واحد غير منقسم ذو طبيعة حركية متغيرة دوما .
المقادير القابلة للقياس والمؤثرات
لا تُرصد لدى إجراء التجارب مواضع الجسيمات فحسب، وإنما تقاس في معظم الأحيان مقادير أخرى انفرادية أو جماعية: مثل الاندفاع والاندفاع الزاوي والطاقة…. .إلخ. وفي كثير من الأحيان تتغير هذه المقادير تبعاً لإحداثيات الجسيمات، وبما أن هذه الأخيرة لا يمكن حسابها بصورة دقيقة فلا يمكن إذن تعيين سوى القيمة الوسطية لمقدار ما، مثل المقدار A، وهي قيمة وسطية مأخوذة بالنسبة إلى مواضع الجسيم المختلفة مع الأخذ بالحسبان احتمال كل منها. وللقيام بقياس المقدار ينبغي إجراء عملية معينة على الجملة الفيزيائية المدروسة. وبالإمكان تمثيل هذه العملية في النظرية الكمومية بمؤثر operator رياضي يُرمز له عادة بالحرف نفسه A كما للمقدار . ويرمز هذا المؤثر إلى طريقة معينة لتحويل دوال المكان والزمانψ (x, y, z, t ) إلى دوال أخرى، أي إنه يحـدد طريقة تتيح اسـتعاضة كل دالـة ψ (x, y, z, t) بدالة أخرى تُحسب منها. وكمثال على ذلك: إن اندفاع جسيم هو المتجه...... ، ....حيث m كتلة الجسيم و... .... سرعته، ومركباته على المحاور الإحداثية هي px و py و pz وهي ثلاثة مقادير قابلة للقياس تجريبياً. يمثَّل المقدار القابل للقياس بالمؤثر:
حيث i العدد التخيلي و h ثابتة بلانك h مقسومة على 2π. ومعنى تطبيق هذا المؤثر على الدالة ψ هو الاستبدال بها الدالة التي يُحصل عليها بضرب مشتقها بالنسبة إلى x بالعدد -ih:
ويمكن - بعد معرفة المؤثر الممثل للمقدار A - تطبيق القاعدة الآتية التي تتيح حساب القيمة الوسطية <A>: يُحسب تكامل جداء الدالة الموجية المرافق العقدي ψ* والدالة على الفضاء كله:
ويمكن أن تكون نتيجة التحويل الذي تخضع له الدالة ψ تحت تأثير المؤثر بسيطة جداً إذا كانت للدالة ψ أشكال معينة خاصة. فيمكن مثلاً إيجاد دالة ψ (x, y, z, t)كون تأثير المؤثر فيها هو تحويلها إلى نفسها مضروبة بمعامل عددي a:
فيقال عندئذ إن هذه الدالة هي دالة ذاتية eigenfunction للمؤثر ، وإن المعامل a هو القيمة الذاتية eigenvalue المقابلة. فإذا كانت الجملة المدروسة في حالة ممثَّلة بالدالة ψ قيل إنها في حالة ذاتية للمؤثر، وكثيراً ما يُستخدم المصطلحان «حالة ذاتية، ودالة ذاتية» للدلالة على الشيء نفسه. وبتطبيق التعريف المذكور سابقاً للقيمة الوسطية *يصبح من السهل رؤية أن القيمة الوسطية في الحالة الذاتية ψ تساوي القيمة الذاتية a المقابلة، وتكون نتيجة قياس المقدار الفيزيائي Aفي هذه الحالة مؤكدة وليست احتمالية.
حساب الدوال الذاتية - معادلة شرودنگر
كان شرودنگر هو الذي أوجد طريقة حساب الدالة الموجية لجملة فيزيائية، وأوجد كيفية تطورها مع الزمن. فقد استرشد بمبدأ التقابل، ووسع الميكانيك الكلاسيكي الذي يستخدم في معادلاته العامة دالة هاملتون H التابعة لإحداثيات جملة الجسيمات x و y و z ومركبات اندفاعها px و py و pz. ويُبرهَن على أن قيمة هذه الدالة تبقى ثابتة في تطور الجملة مع مرور الزمن، وهي تساوي طاقة الجملة الكلية. وفي الحالة البسيطة جداً التي تكون الجملة فيها مؤلفة من جسيم واحد كتلته m خاضع للقوة التي تُشتق من طاقة كامنة V (x, y, z)
تُحسب دالة هاملتون من العلاقة:
واستناداً إلى دالة هاملتون الكلاسيكية هذه يُشَكل مؤثر هاملتون..... ...
بمجرد استعاضة المقادير pxو py و pz بالمؤثرات
ففي حالة جسيم وحيد يكون المؤثر الهاملتوني على الشكل:
ويعتمد تطور الجملة الفيزيائية مع الزمن على المؤثر الهاملتوني؛ وهذا ما تعنيه معادلة شرودنگر:
وفي معظم الأحيان لا يعتمد المؤثر نفسه على الزمن، وهذا يعني أن أية دالة لا تعتمد على الزمن هي تابع ذاتي للمؤثر. وهذا يؤدي إلى أن من بين الحلول الممكنة لهذه المعادلة ذات المشتقات الجزئية هناك فئة ذات أهمية خاصة هي الحلول المستقرة. وبالتشابه مع الأمواج المستقرة التي تتغير بصورة جيبية مع الزمن، وتكون سعتها ثابتة مستقلة عن الزمن، وإنما متغيرة من نقطة إلى أخرى. تعطى التوابع الموجية المستقرة بالعلاقة:
ψ (x, y, z, t) = ψ (x, y, z)e-i ω t
التي فيها الدالة مستقلة عن الزمن، وتدعى الدالة الموجية المستقلة عن الزمن أو سعة الاحتمال بالتشابه مع سعة موجة جيبية كلاسيكية. ويُبرهَن على أنه يمكن التعبير عن أي حل Ψلهذه المعادلة على شكل مجموع حلول مستقرة. ولهذا توضع ψ (x, y, z, t)e-i ω t مكان الدالة ψ (x, y, z, t) في معادلة شرودنغر التابعة للزمن، وباختصار الدالة e-i ω t ووضع h ω = E يُحصل على معادلة شرودنغر المستقلة عن الزمن:
وهذه المعادلة تعني أن الدالة ψ يجب أن تكون دالة ذاتية للمؤثر..؛ وأن الحالات المستقرة للجملة المدروسة هي الحالات الذاتية للمؤثر الهاملتوني. أما القيم الذاتية E المقابلة فهي تمثل قيم طاقة الجملة في كل من هذه الحالات، وليست المعادلة السابقة سوى معادلة القيم الذاتية للمؤثر الهاملتوني.[1]
المصادر
- موسوعة ويكيبيديا (الانكليزية ، الالمانية)
- موجز تاريخ الزمن : Brief History of Time ، Stephen Hawking
- العوالم الاخرى : Other Worlds ، Paul Davies
انظر أيضاً
- قائمة مواضيع الكم
- نصف قطر بور
- تموج كمومي
- مبدأ عدم التأكد
- تحلل ألفا
- حالة قاعية
- حالة إثارة
- معامل لاندي
- نفق ميكانيكا الكم
- EPR paradox
- Macroscopic quantum phenomena
الهوامش
- ^ بسام المعصراني. "ميكانيك الكم". الموسوعة العربية.
المصادر
The following titles, all by working physicists, attempt to communicate quantum theory to lay people, using a minimum of technical apparatus.
- Malin, Shimon (2012). Nature Loves to Hide: Quantum Physics and the Nature of Reality, a Western Perspective (Revised Edition). World Scientific. ISBN 978-981-4324-57-1
- Chester, Marvin (1987) Primer of Quantum Mechanics. John Wiley. ISBN 0-486-42878-8
- Richard Feynman, 1985. QED: The Strange Theory of Light and Matter, Princeton University Press. ISBN 0-691-08388-6. Four elementary lectures on quantum electrodynamics and quantum field theory, yet containing many insights for the expert.
- Ghirardi, GianCarlo, 2004. Sneaking a Look at God's Cards, Gerald Malsbary, trans. Princeton Univ. Press. The most technical of the works cited here. Passages using algebra, trigonometry, and bra-ket notation can be passed over on a first reading.
- N. David Mermin, 1990, "Spooky actions at a distance: mysteries of the QT" in his Boojums all the way through. Cambridge University Press: 110-76.
- Victor Stenger, 2000. Timeless Reality: Symmetry, Simplicity, and Multiple Universes. Buffalo NY: Prometheus Books. Chpts. 5-8. Includes cosmological and philosophical considerations.
More technical:
- Bryce DeWitt, R. Neill Graham, eds., 1973. The Many-Worlds Interpretation of Quantum Mechanics, Princeton Series in Physics, Princeton University Press. ISBN 0-691-08131-X
- Dirac, P. A. M. (1930). The Principles of Quantum Mechanics. ISBN 0-19-852011-5. The beginning chapters make up a very clear and comprehensible introduction.
- Hugh Everett, 1957, "Relative State Formulation of Quantum Mechanics," Reviews of Modern Physics 29: 454-62.
- Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (1965). The Feynman Lectures on Physics. Vol. 1–3. Addison-Wesley. ISBN 0-7382-0008-5.
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-111892-7. OCLC 40251748. A standard undergraduate text.
- Max Jammer, 1966. The Conceptual Development of Quantum Mechanics. McGraw Hill.
- Hagen Kleinert, 2004. Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 3rd ed. Singapore: World Scientific. Draft of 4th edition.
- Gunther Ludwig, 1968. Wave Mechanics. London: Pergamon Press. ISBN 0-08-203204-1
- George Mackey (2004). The mathematical foundations of quantum mechanics. Dover Publications. ISBN 0-486-43517-2.
- Albert Messiah, 1966. Quantum Mechanics (Vol. I), English translation from French by G. M. Temmer. North Holland, John Wiley & Sons. Cf. chpt. IV, section III.
- Omnès, Roland (1999). Understanding Quantum Mechanics. Princeton University Press. ISBN 0-691-00435-8. OCLC 39849482.
- Scerri, Eric R., 2006. The Periodic Table: Its Story and Its Significance. Oxford University Press. Considers the extent to which chemistry and the periodic system have been reduced to quantum mechanics. ISBN 0-19-530573-6
- Transnational College of Lex (1996). What is Quantum Mechanics? A Physics Adventure. Language Research Foundation, Boston. ISBN 0-9643504-1-6. OCLC 34661512.
- von Neumann, John (1955). Mathematical Foundations of Quantum Mechanics. Princeton University Press. ISBN 0-691-02893-1.
- Hermann Weyl, 1950. The Theory of Groups and Quantum Mechanics, Dover Publications.
- D. Greenberger, K. Hentschel, F. Weinert, eds., 2009. Compendium of quantum physics, Concepts, experiments, history and philosophy, Springer-Verlag, Berlin, Heidelberg.
قراءات أخرى
- Bernstein, Jeremy (2009). Quantum Leaps. Cambridge, Massachusetts: Belknap Press of Harvard University Press. ISBN 978-0-674-03541-6.
- Bohm, David (1989). Quantum Theory. Dover Publications. ISBN 0-486-65969-0.
- Eisberg, Robert; Resnick, Robert (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd ed.). Wiley. ISBN 0-471-87373-X.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Liboff, Richard L. (2002). Introductory Quantum Mechanics. Addison-Wesley. ISBN 0-8053-8714-5.
- Merzbacher, Eugen (1998). Quantum Mechanics. Wiley, John & Sons, Inc. ISBN 0-471-88702-1.
- Sakurai, J. J. (1994). Modern Quantum Mechanics. Addison Wesley. ISBN 0-201-53929-2.
- Shankar, R. (1994). Principles of Quantum Mechanics. Springer. ISBN 0-306-44790-8.
- Cox, Brian; Forshaw, Jeff (2011). The Quantum Universe: Everything That Can Happen Does Happen. Allen Lane. ISBN 1-84614-432-9.
وصلات خارجية
- ميكانيكا الكم (موسوعة ستانفورد للفلسفة)
- ملاحظات حول ميكانيكا الكم
- ميكانيكا الكم
- كل شيء تريد معرفته عن العالم الكمومي — من مجلة العالم الجديد.
- تاريخ ميكانيك الكم
- ديفيد ميرمين يكتب عن التوجهات المستقبلية للفيزياء
- تطورات جديدة في فهم العلاقة بين الفيزياء الكلاسكية-الكمومية
- المرشد للفيزياء الكمومية
- أسئلة متكررة حول الرنين الكمومي
- مجموعة دروس قابلة للتنزيل حول ميكانيك الكم
- مقدمة للميكانيك الكمومي
- “Quantum Trickery: Testing Einstein's Strangest Theory,” نيويورك تايمز, 27 ديسمبر, 2005.
- محاضرات ثلاث لهانز بيثي
| Find more about ميكانيكا الكم at Wikipedia's sister projects | |
| Definitions from Wiktionary | |
| Media from Commons | |
| Quotations from Wikiquote | |
| Source texts from Wikisource | |
| Textbooks from Wikibooks | |
| Learning resources from Wikiversity | |
- Quantum Cook Book by R. Shankar, Open Yale PHYS 201 material (4pp)
- A foundation approach to quantum Theory that does not rely on wave-particle duality.
- The Modern Revolution in Physics - an online textbook.
- J. O'Connor and E. F. Robertson: A history of quantum mechanics.
- Introduction to Quantum Theory at Quantiki.
- Quantum Physics Made Relatively Simple: three video lectures by Hans Bethe
- H is for h-bar.
- Quantum Mechanics Books Collection: Collection of free books
- Course material
- Doron Cohen: Lecture notes in Quantum Mechanics (comprehensive, with advanced topics).
- MIT OpenCourseWare: Chemistry.
- MIT OpenCourseWare: Physics. See 8.04
- Stanford Continuing Education PHY 25: Quantum Mechanics by Leonard Susskind, see course description Fall 2007
- 5½ Examples in Quantum Mechanics
- Imperial College Quantum Mechanics Course.
- Spark Notes - Quantum Physics.
- Quantum Physics Online : interactive introduction to quantum mechanics (RS applets).
- Experiments to the foundations of quantum physics with single photons.
- AQME : Advancing Quantum Mechanics for Engineers — by T.Barzso, D.Vasileska and G.Klimeck online learning resource with simulation tools on nanohub
- Quantum Mechanics by Martin Plenio
- Quantum Mechanics by Richard Fitzpatrick
- Online course on Quantum Transport
- FAQs
- Media
- PHYS 201: Fundamentals of Physics II by Ramamurti Shankar, Open Yale Course
- Lectures on Quantum Mechanics by Leonard Susskind
- Everything you wanted to know about the quantum world — archive of articles from New Scientist.
- Quantum Physics Research from Science Daily
- Overbye, Dennis (December 27, 2005). "Quantum Trickery: Testing Einstein's Strangest Theory". The New York Times. Retrieved April 12, 2010.
- Audio: Astronomy Cast Quantum Mechanics — June 2009. Fraser Cain interviews Pamela L. Gay.
- Philosophy
| Quantum mechanics
]].