تشابك كمي
| جزء من سلسلة مقالات عن |
| ميكانيكا الكم |
|---|
التشابك الكمي Quantum entanglement، هي ظاهرة فيزيائية ترتبط فيها الجسيمات الكميّة (مثل الفوتونات والإلكترونات والجزيئات) ببعضها، رغم وجود مسافات كبيرة تفصل بينها.[1][2][3] مما يقود إلى ارتباطات في الخواص الفيزيائية المقيسة لهذه الجسيمات الكمّية.
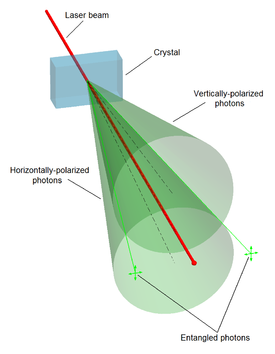
يمكن على سبيل المثال أن نجعل جسيمين في حالة كمّية مفردة بحيث يكونا متعاكسين حتما في دورانهم (spin)، فإذا قسنا دوران أحدهما وتبين أنه ذو دوران علوي فالآخر حتما سفلي الدوران ، وبالعكس. يجب أن نتذكر هنا أن نتيجة القياس للجسيم الكمومي عشوائية تماما حسب تفسير كوبنهاغن المعتمد ولا يمكن التنبؤ بنتائج هذا القياس، ومع ذلك فإن عملية القياس المجراة على جملة كمومية تؤثر آنيا على جمل كمومية أخرى متشابكة مع الأولى.
رغم أن سرعة نقل المعلومات هنا تخرق مبدأ سرعة الضوء العظمى في النسبية فإنه لا يمكن نقل معلومات كلاسيكية عن طريق التشابك الكمّي مما يسمح بالحفاظ على النظرية النسبية .
هذه الظاهرة كانت موضوعاً للورقة البحثية التي كتبها ألبرت أينشتاين، بوريس پودولسكي، وناثان روزن عام 1935، [4] والعديد من الأوراق البحثية التي كتبها إرڤن شرودنگر بعد ذلك بفترة وجيزة،[5][6] تصفح ما يعرف اليوم باسم EPR paradox. اعتبر أينشتاين وآخرون مثل هذا السلوك أنه مستحيلاً، حيث يعتبر انتهاكاً للنظرة الواقعية المحلية للسببية (أشار أينشتاين لهذا باعتباره "spooky action at a distance")[7] وجادل في أن الصيغة المقبولة من ميكانيكا الكم ينبغي أن تكون غير كاملة. لاحقاً، تم التحقق من التنبؤات غير المتوقعة من ميكانيكا الكم تجريبياً[8] من خلال الاختبارات التي جرى فيها قياس استقطاب أو دوران الجسيمات المتشابكة في مواقع منفصلة، منتهكة إحصائياً مبرهنة بل، وأثبتت أن المفهوم الكلاسيكي "للواقعية المحلية" لا يمكن أن يكون صحيحاً.
Later, however, the counterintuitive predictions of quantum mechanics were verified experimentally[9][10][11] in tests in which polarization or spin of entangled particles were measured at separate locations, statistically violating Bell's inequality. In earlier tests, it couldn't be absolutely ruled out that the test result at one point could have been subtly transmitted to the remote point, affecting the outcome at the second location.[11] However, so-called "loophole-free" Bell tests have been performed in which the locations were separated such that communications at the speed of light would have taken longer--in one case 10,000 times longer—than the interval between the measurements.[10][9]
According to some interpretations of quantum mechanics, the effect of one measurement occurs instantly. Other interpretations which don't recognize wavefunction collapse dispute that there is any "effect" at all. However, all interpretations agree that entanglement produces correlation between the measurements and that the mutual information between the entangled particles can be exploited, but that any transmission of information at faster-than-light speeds is impossible.[12][13]
Quantum entanglement has been demonstrated experimentally with photons,[14][15][16][17][18][19][20] neutrinos,[21] electrons,[22][23] molecules as large as buckyballs,[24][25] and even small diamonds.[26][27] The utilization of entanglement in communication, computation and quantum radar is a very active area of research and development.
التاريخ

المفهوم
معنى التشابك
المفارقة
نظرية المتغيرات المخفية
انتهاكات مبرهنة بل
أنواع أخرى من التجارب
لغز الزمن
مصدر مصفوفة الزمن
الجاذبية الناشئة
اللا موضعية والتشابك
إطار عمل ميكانيكا الكم
الأطوار النقية
- .
المجموعات
المصفوفات منخفضة الكثافة
- .
- .
التطبيقان المستخدمان
التشابك كمصدر
تصنيف التشابك
العشوائي الداخلي
تعريف
- .
كمقياس للتشابك
Indeed, without this property, the von Neumann entropy would not be well-defined.
In particular, U could be the time evolution operator of the system, i.e.,
مقاييس التشابك
Entanglement measures quantify the amount of entanglement in a (often viewed as a bipartite) quantum state. As aforementioned, entanglement entropy is the standard measure of entanglement for pure states (but no longer a measure of entanglement for mixed states). For mixed states, there are some entanglement measures in the literature[28] and no single one is standard.
- Entanglement cost
- Distillable entanglement
- Entanglement of formation
- Relative entropy of entanglement
- Squashed entanglement
- Logarithmic negativity
Most (but not all) of these entanglement measures reduce for pure states to entanglement entropy, and are difficult (NP-hard) to compute.[29]
نظرية المجال الكمي
تطبيقات
Entanglement has many applications in quantum information theory. With the aid of entanglement, otherwise impossible tasks may be achieved.
Among the best-known applications of entanglement are superdense coding and quantum teleportation.[30]
Most researchers believe that entanglement is necessary to realize quantum computing (although this is disputed by some).[31]
Entanglement is used in some protocols of quantum cryptography.[32][33] This is because the "shared noise" of entanglement makes for an excellent one-time pad. Moreover, since measurement of either member of an entangled pair destroys the entanglement they share, entanglement-based quantum cryptography allows the sender and receiver to more easily detect the presence of an interceptor.[citation needed]
In interferometry, entanglement is necessary for surpassing the standard quantum limit and achieving the Heisenberg limit.[34]
الأطوار المتشابكة
There are several canonical entangled states that appear often in theory and experiments.
For two qubits, the Bell states are
- .
These four pure states are all maximally entangled (according to the entropy of entanglement) and form an orthonormal basis (linear algebra) of the Hilbert space of the two qubits. They play a fundamental role in Bell's theorem.
For M>2 qubits, the GHZ state is
which reduces to the Bell state for . The traditional GHZ state was defined for . GHZ states are occasionally extended to qudits, i.e., systems of d rather than 2 dimensions.
Also for M>2 qubits, there are spin squeezed states.[35] Spin squeezed states are a class of squeezed coherent states satisfying certain restrictions on the uncertainty of spin measurements, and are necessarily entangled.[36] Spin squeezed states are good candidates for enhancing precision measurements using quantum entanglement.[37]
For two bosonic modes, a NOON state is
This is like the Bell state except the basis kets 0 and 1 have been replaced with "the N photons are in one mode" and "the N photons are in the other mode".
Finally, there also exist twin Fock states for bosonic modes, which can be created by feeding a Fock state into two arms leading to a beam splitter. They are the sum of multiple of NOON states, and can used to achieve the Heisenberg limit.[38]
For the appropriately chosen measure of entanglement, Bell, GHZ, and NOON states are maximally entangled while spin squeezed and twin Fock states are only partially entangled. The partially entangled states are generally easier to prepare experimentally.
طرق خلق التشابك
اختبار النظام من أجل التشابك
الأنظمة المتشابكة طبيعياً
البناء الضوئي
الأنظمة الحية
In October 2018, physicists reported producing quantum entanglement using living organisms, particularly between living bacteria and quantized light.[39][40]
Living organisms (green sulphur bacteria) have been studied as mediators to create quantum entanglement between otherwise non-interacting light modes, showing high entanglement between light and bacterial modes, and to some extent, even entanglement within the bacteria.[41]
تجارب حديثة
في تمكن العلماء من دمج ذاكرتين كموميتين بينهما مسافة أكبر بكثير، مما تم تجربته من قبل، الأمر الذي يعتبر إنجازاً قد يغير طريقة عمل الإنترنت في يوم ما.[42]
يمكن أن يكون الاكتشاف خطوة كبيرة نحو الإنترنت الكمومي، على الرغم من أنه يعد مبكراً للغاية. ويأمل العلماء في أن يسمح الاكتشاف بتطور التشابك عبر المسافات الطويلة وعدد من العقد، والتي ستكون ضرورية لمثل هذه الشبكة.
لطالما كان الباحثون يأملون في تطوير شبكة إنترنت كمومية، وإنشاء نوع جديد من الشبكات التي تستخدم السلوك غير العادي للعالم الكمومي لنقل البيانات بسرعات وأمان محسَّنين إلى حد كبير.
تعمل الشبكة الكمومية بفكرة مشابهة للإنترنت التقليدي، مما يتيح توصيل كميات كبيرة من البيانات عبر مسافات طويلة. لكنها ستفعل ذلك باستخدام وحدات البت الكمومي، أو الكيوبت، بين المعالجات الكمومية - تقديم أنواع جديدة من الاحتمالات بالإضافة إلى الإنترنت الكلاسيكي الحالي.
ولكن للقيام بذلك، ستحتاج تلك الشبكات إلى أن تكون قادرة على نقل الجسيمات المتشابكة، وهي ظاهرة "عصبية" تسمح للجزيئات بالتأثير على بعضها البعض على مسافات كبيرة. في السنوات الأخيرة، كانت هناك تجارب اختراقية للقيام بذلك - والتي سمحت للباحثين بنقل الجسيمات المتشابكة عبر الكابلات أو باستخدام الأقمار الصناعية - ولكن تم تقييدها جميعاً على بعد.
عند استخدام النقل الكمومي عبر هذه المسافة الطويلة، غالباً لا ينجح التوزيع، لأن عمليات الإرسال تضيع وبالتالي لا يمكنها التواصل بشكل موثوق.
حتى الآن، فإن أبعد مسافة تمكن العلماء خلالها من إقامة تشابك للذاكرات الكمومية هو 1.3 كيلومتر. يشير ذلك إلى احتمال وجود صعوبات في توسيع نطاق هذا النظام إلى نطاق يمكن استخدامه فعلياً، مثل إرسال البيانات عبر المدينة.
في هذا البحث الجديد، تمكن المهندسون من نقل الجزيئات المتشابكة على مسافة أكبر بكثير من 50 كم. لقد فعلوا ذلك باستخدام تأثير كمومي معين يسمح بالانتقال بطول محسّن بشكل كبير.
عبر هذه المسافة قد يُسمح بالنقل على مسافات طويلة من النوع الذي يمكن أن يربط المدن ببعضها البعض وتعمل أخيراً على تحقيق حلم الإنترنت الكمومي، وفقاً لما كتبه الباحثون في الورقة البحثية الجديدة التي نشرت في مجلة نيتشر.
وحسب ما جاء في البحث: "إن توسيع نطاق هذه التجارب لتشمل العقد التي تفصل بينها مسافات أطول بكثير ستمكننا من أداء مهام المعلومات الكمومية المتقدمة، مثل النقل الكمومي الفعال عبر المسافات الطويلة".
في هذه الدراسة، درس الباحثون في الكيفية التي يمكن أن ينقلوا بها ذاكرتين كموميتين، وهي النسخة الكمومية من ذاكرة الحاسوب العادية، أو ما يعادلها من ذاكرة القرص الصلب. في حين أن قطعة من ذاكرة الحاسوب ستخزن المعلومات على أنها 1 ثانية أو 0 ثانية، فإن الذاكرة الكمومية ستحتفظ بالحالة الكمومية، مما يسمح نظرياً بحوسبة أكثر قوة.
للتشابك بين هاتين الذاكرتين الكموميتين، اضطر الباحثون إلى إطلاق فوتونات، أو جزيئات فردية من الضوء، على طول الكابل البالغ طوله 50 كيلومتر. بعد شق طريقهما عبر تلك المسافة، تمكنت الذاكرتان من التداخل مع بعضهما البعض، مما أدى إلى نجاح التجربة وإظهار أنه يمكن أن تتشابك ذاكرتان كموميتان على هذه المسافة.
انظر أيضاً
- بوابة الكم المراقبة
- Concurrence (quantum computing)
- Einstein's thought experiments
- Entanglement distillation
- Entanglement witness
- Faster-than-light communication
- Ghirardi–Rimini–Weber theory
- Multipartite entanglement
- Normally distributed and uncorrelated does not imply independent
- Observer effect (physics)
- Quantum coherence
- Quantum discord
- Quantum phase transition
- الحوسبة الكمومية
- Quantum pseudo-telepathy
- انتقال آني كمي
- Retrocausality
- Separable state
- Squashed entanglement
- Ward's probability amplitude
- Wheeler–Feynman absorber theory
المصادر
- ^ Jaeger G, Shimony A, Vaidman L; Shimony; Vaidman (1995). "Two Interferometric Complementarities". Phys. Rev. 51 (1): 54–67. Bibcode:1995PhRvA..51...54J. doi:10.1103/PhysRevA.51.54.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Quantum entanglement shows that reality can't be local, Ars Technica, 30 October 2012 Archived 2017-09-25 at the Wayback Machine
- ^ Einstein A, Podolsky B, Rosen N; Podolsky; Rosen (1935). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?". Phys. Rev. 47 (10): 777–780. Bibcode:1935PhRv...47..777E. doi:10.1103/PhysRev.47.777.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^
Einstein A, Podolsky B, Rosen N; Podolsky; Rosen (1935). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?" (PDF). Phys. Rev. 47 (10): 777–780. Bibcode:1935PhRv...47..777E. doi:10.1103/PhysRev.47.777.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Schrödinger E (1935). "Discussion of probability relations between separated systems". Mathematical Proceedings of the Cambridge Philosophical Society. 31 (4): 555–563. Bibcode:1935PCPS...31..555S. doi:10.1017/S0305004100013554.
- ^ Schrödinger E (1936). "Probability relations between separated systems". Mathematical Proceedings of the Cambridge Philosophical Society. 32 (3): 446–452. Bibcode:1936PCPS...32..446S. doi:10.1017/S0305004100019137.
- ^ Physicist John Bell depicts the Einstein camp in this debate in his article entitled "Bertlmann's socks and the nature of reality", p. 143 of Speakable and unspeakable in quantum mechanics: "For EPR that would be an unthinkable 'spooky action at a distance'. To avoid such action at a distance they have to attribute, to the space-time regions in question, real properties in advance of observation, correlated properties, which predetermine the outcomes of these particular observations. Since these real properties, fixed in advance of observation, are not contained in quantum formalism, that formalism for EPR is incomplete. It may be correct, as far as it goes, but the usual quantum formalism cannot be the whole story." And again on p. 144 Bell says: "Einstein had no difficulty accepting that affairs in different places could be correlated. What he could not accept was that an intervention at one place could influence, immediately, affairs at the other." Downloaded 5 July 2011 from Bell, J. S. (1987). Speakable and Unspeakable in Quantum Mechanics (PDF). CERN. ISBN 0521334950. Archived from the original (PDF) on 12 أبريل 2015. Retrieved 14 يونيو 2014.
{{cite book}}: Unknown parameter|deadurl=ignored (|url-status=suggested) (help) - ^ "75 years of entanglement – Science News". 23 سبتمبر 2013. Retrieved 13 أكتوبر 2014.
- ^ أ ب Yin, Juan; Cao, Yuan; Yong, Hai-Lin; Ren, Ji-Gang; Liang, Hao; Liao, Sheng-Kai; Zhou, Fei; Liu, Chang; Wu, Yu-Ping; Pan, Ge-Sheng; Li, Li; Liu, Nai-Le; Zhang, Qiang; Peng, Cheng-Zhi; Pan, Jian-Wei (2013). "Bounding the speed of 'spooky action at a distance". Physical Review Letters. 110 (26): 260407. arXiv:1303.0614. Bibcode:2013PhRvL.110z0407Y. doi:10.1103/PhysRevLett.110.260407. PMID 23848853. S2CID 119293698.
- ^ أ ب Matson, John (13 أغسطس 2012). "Quantum teleportation achieved over record distances". Nature News. doi:10.1038/nature.2012.11163. S2CID 124852641.
- ^ أ ب Francis, Matthew. Quantum entanglement shows that reality can't be local, Ars Technica, 30 October 2012
- ^ Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, London, 2004, p. 603.
- ^ Griffiths, David J. (2004), Introduction to Quantum Mechanics (2nd ed.), Prentice Hall, ISBN 978-0-13-111892-8
- ^ Kocher, CA; Commins, ED (1967). "Polarization Correlation of Photons Emitted in an Atomic Cascade". Physical Review Letters. 18 (15): 575–577. Bibcode:1967PhRvL..18..575K. doi:10.1103/PhysRevLett.18.575.
- ^ Carl A. Kocher, Ph.D. Thesis (University of California at Berkeley, 1967). Polarization Correlation of Photons Emitted in an Atomic Cascade
- ^ Kocher, CA (1971). "Time correlations in the detection of successively emitted photons". Annals of Physics. 65 (1): 1–18. Bibcode:1971AnPhy..65....1K. doi:10.1016/0003-4916(71)90159-X.
- ^ Kwiat, PG; Mattle, K; Weinfurter, H; Zeilinger, A; Sergienko, AV; Shih, Y (1995). "New High-Intensity Source of Polarization-Entangled Photon Pairs". Physical Review Letters. 75 (24): 4337–4341. Bibcode:1995PhRvL..75.4337K. doi:10.1103/PhysRevLett.75.4337. PMID 10059884.
- ^ Zhao, Z; Chen, YA; Zhang, AN; Yang, T; Briegel, HJ; Pan, JW (يوليو 2004). "Experimental demonstration of five-photon entanglement and open-destination teleportation". Nature. 430 (6995): 54–58. arXiv:quant-ph/0402096. Bibcode:2004Natur.430...54Z. doi:10.1038/nature02643. PMID 15229594. S2CID 4336020.
- ^ Lu, Chao-Yang (2007). "Experimental entanglement of six photons in graph states". Nature Physics. 3 (2): 91–95. arXiv:quant-ph/0609130. Bibcode:2007NatPh...3...91L. doi:10.1038/nphys507. S2CID 16319327.
- ^ Yao, Xing-Can (2012). "Observation of eight-photon entanglement". Nature Photonics. 6 (4): 225–228. arXiv:1105.6318. Bibcode:2012NaPho...6..225Y. doi:10.1038/nphoton.2011.354. S2CID 118510047.
- ^ J. A. Formaggio, D. I. Kaiser, M. M. Murskyj, and T. E. Weiss (2016), "Violation of the Leggett-Garg inequality in neutrino oscillations". Phys. Rev. Lett. Accepted 23 June 2016.
- ^ Hensen, B.; et al. (21 أكتوبر 2015). "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres". Nature. 526 (7575): 682–686. arXiv:1508.05949. Bibcode:2015Natur.526..682H. doi:10.1038/nature15759. hdl:2117/79298. PMID 26503041. S2CID 205246446. See also free online access version.
- ^ Markoff, Jack (21 أكتوبر 2015). "Sorry, Einstein. Quantum Study Suggests 'Spooky Action' Is Real". The New York Times. Retrieved 21 أكتوبر 2015.
- ^ Arndt, M; Nairz, O; Vos-Andreae, J; Keller, C; van der Zouw, G; Zeilinger, A (14 أكتوبر 1999). "Wave–particle duality of C60 molecules". Nature. 401 (6754): 680–682. Bibcode:1999Natur.401..680A. doi:10.1038/44348. PMID 18494170. S2CID 4424892. (يتطلب اشتراك)
- ^ Olaf Nairz, Markus Arndt, and Anton Zeilinger, "Quantum interference experiments with large molecules", American Journal of Physics, 71 (April 2003) 319–325.
- ^ Lee, K. C.; Sprague, M. R.; Sussman, B. J.; Nunn, J.; Langford, N. K.; Jin, X.- M.; Champion, T.; Michelberger, P.; Reim, K. F.; England, D.; Jaksch, D.; Walmsley, I. A. (2 ديسمبر 2011). "Entangling macroscopic diamonds at room temperature". Science. 334 (6060): 1253–1256. Bibcode:2011Sci...334.1253L. doi:10.1126/science.1211914. PMID 22144620. S2CID 206536690.
{{cite journal}}: Unknown parameter|lay-url=ignored (help) - ^ sciencemag.org, supplementary materials
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةarxiv.org - ^ Huang, Yichen (21 مارس 2014). "Computing quantum discord is NP-complete". New Journal of Physics. 16 (3): 033027. arXiv:1305.5941. Bibcode:2014NJPh...16c3027H. doi:10.1088/1367-2630/16/3/033027. S2CID 118556793.
- ^ Bouwmeester, Dik; Pan, Jian-Wei; Mattle, Klaus; Eibl, Manfred; Weinfurter, Harald; Zeilinger, Anton (1997). "Experimental Quantum Teleportation" (PDF). Nature. 390 (6660): 575–579. arXiv:1901.11004. Bibcode:1997Natur.390..575B. doi:10.1038/37539. S2CID 4422887.
{{cite journal}}: Unknown parameter|last-author-amp=ignored (|name-list-style=suggested) (help) - ^ Richard Jozsa; Noah Linden (2002). "On the role of entanglement in quantum computational speed-up". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 459 (2036): 2011–2032. arXiv:quant-ph/0201143. Bibcode:2003RSPSA.459.2011J. CiteSeerX 10.1.1.251.7637. doi:10.1098/rspa.2002.1097. S2CID 15470259.
- ^ Ekert, Artur K. (1991). "Quantum cryptography based on Bell's theorem" (PDF). Physical Review Letters. 67 (6): 661–663. Bibcode:1991PhRvL..67..661E. doi:10.1103/PhysRevLett.67.661. PMID 10044956. S2CID 27683254.
- ^ Yin, Juan; Cao, Yuan; Yong, Hai-Lin; Ren, Ji-Gang; Liang, Hao; Liao, Sheng-Kai; Zhou, Fei; Liu, Chang; Wu, Yu-Ping; Pan, Ge-Sheng; Zhang, Qiang; Peng, Cheng-Zhi; Pan, Jian-Wei (2010). "Contextuality offers device-independent security". arXiv:1006.0468 [quant-ph].
- ^ Pezze, Luca; Smerzi, Augusto (2009). "Entanglement, Nonlinear Dynamics, and the Heisenberg Limit". Phys. Rev. Lett. 102 (10): 100401. arXiv:0711.4840. Bibcode:2009PhRvL.102j0401P. doi:10.1103/PhysRevLett.102.100401. PMID 19392092. S2CID 13095638.
{{cite journal}}: Unknown parameter|last-author-amp=ignored (|name-list-style=suggested) (help) - ^ Database error – Qwiki Archived 21 أغسطس 2012 at the Wayback Machine
- ^ Kitagawa, Masahiro; Ueda, Masahito (1993). "Squeezed Spin States". Phys. Rev. A. 47 (6): 5138–5143. Bibcode:1993PhRvA..47.5138K. doi:10.1103/physreva.47.5138. PMID 9909547.
- ^ Wineland, D. J.; Bollinger, J. J.; Itano, W. M.; Moore, F. L.; Heinzen, D. J. (1992). "Spin squeezing and reduced quantum noise in spectroscopy". Phys. Rev. A. 46 (11): R6797–R6800. Bibcode:1992PhRvA..46.6797W. doi:10.1103/PhysRevA.46.R6797. PMID 9908086.
- ^ Holland, M. J; Burnett, K (1993). "Interferometric detection of optical phase shifts at the Heisenberg limit". Physical Review Letters. 71 (9): 1355–1358. Bibcode:1993PhRvL..71.1355H. doi:10.1103/PhysRevLett.71.1355. PMID 10055519.
- ^ Marletto, C.; Coles, D.M.; Farrow, T.; Vedral, V. (10 أكتوبر 2018). "Entanglement between living bacteria and quantized light witnessed by Rabi splitting". Journal of Physics: Communications. 2 (10): 101001. arXiv:1702.08075. Bibcode:2018JPhCo...2j1001M. doi:10.1088/2399-6528/aae224. S2CID 119236759.
- ^ O'Callaghan, Jonathan (29 أكتوبر 2018). ""Schrödinger's Bacterium" Could Be a Quantum Biology Milestone – A recent experiment may have placed living organisms in a state of quantum entanglement". Scientific American. Retrieved 29 أكتوبر 2018.
- ^ Krisnanda, T.; Marletto, C.; Vedral, V.; Paternostro, M.; Paterek, T. (2018). "Probing quantum features of photosynthetic organisms". NPJ Quantum Information. 4: 60. doi:10.1038/s41534-018-0110-2.
- ^ "SCIENTISTS MAKE MAJOR BREAKTHROUGH IN 'QUANTUM ENTANGLEMENT' THAT COULD CHANGE HOW THE INTERNET WORKS". إندپندنت. 15 فبراير 2020. Retrieved 16 فبراير 2020.
قراءات إضافية
- Bengtsson I; Życzkowski K (2006). "Geometry of Quantum States". An Introduction to Quantum Entanglement. Cambridge: Cambridge University Press. second, revised edition (2017)
- Cramer, JG (2015). The Quantum Handshake: Entanglement, Nonlocality and Transactions. Springer Verlag. ISBN 978-3-319-24642-0.
- Gühne, O.; Tóth, G. (2009). "Entanglement detection". Physics Reports. 474 (1–6): 1–75. arXiv:0811.2803. Bibcode:2009PhR...474....1G. doi:10.1016/j.physrep.2009.02.004.
- Horodecki R, Horodecki P, Horodecki M, Horodecki K; Horodecki; Horodecki; Horodecki (2009). "Quantum entanglement". Rev. Mod. Phys. 81 (2): 865–942. arXiv:quant-ph/0702225. Bibcode:2009RvMP...81..865H. doi:10.1103/RevModPhys.81.865.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Jaeger G (2009). Entanglement, Information, and the Interpretation of Quantum Mechanics. Heildelberg: Springer. ISBN 978-3-540-92127-1.
- Plenio MB, Virmani S; Virmani (2007). "An introduction to entanglement measures". Quant. Inf. Comp. 1 (7): 1–51. arXiv:quant-ph/0504163. Bibcode:2005quant.ph..4163P.
- Shadbolt PJ, Verde MR, Peruzzo A, Politi A, Laing A, Lobino M, Matthews JCF, Thompson MG, O'Brien JL; Verde; Peruzzo; Politi; Laing; Lobino; Matthews; Thompson; O'Brien (2012). "Generating, manipulating and measuring entanglement and mixture with a reconfigurable photonic circuit". Nature Photonics. 6 (1): 45–59. arXiv:1108.3309. Bibcode:2012NaPho...6...45S. doi:10.1038/nphoton.2011.283.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Steward EG (2008). Quantum Mechanics: Its Early Development and the Road to Entanglement. Imperial College Press. ISBN 978-1-86094-978-4.
- Vedral, V. (2002). "The role of relative entropy in quantum information theory". Reviews of Modern Physics. 74 (1): 197–234. arXiv:quant-ph/0102094. Bibcode:2002RvMP...74..197V. doi:10.1103/RevModPhys.74.197.
وصلات خارجية
- The original EPR paper
- Quantum Entanglement at Stanford Encyclopedia of Philosophy
- How to entangle photons experimentally (subscription required)
- A creative interpretation of Quantum Entanglement
- Albert's chest: entanglement for lay persons
- How Quantum Entanglement Works
- Explanatory video by Scientific American magazine
- Hanson Lab – Loophole-free Bell test ‘Spooky action at a distance’, no cheating.
- Two Diamonds Linked by Strange Quantum Entanglement
- Entanglement experiment with photon pairs – interactive
- Multiple entanglement and quantum repeating
- Quantum Entanglement and Bell's Theorem at MathPages
- Audio – Cain/Gay (2009) Astronomy Cast Entanglement
- Recorded research seminars at Imperial College relating to quantum entanglement
- Quantum Entanglement and Decoherence: 3rd International Conference on Quantum Information (ICQI)
- Ion trapping quantum information processing
- IEEE Spectrum On-line: The trap technique
- Was Einstein Wrong?: A Quantum Threat to Special Relativity
- Citizendium: Entanglement
- Spooky Actions At A Distance?: Oppenheimer Lecture, Prof. David Mermin (Cornell University) Univ. California, Berkeley, 2008. Non-mathematical popular lecture on YouTube, posted Mar 2008
- "StateSeparator" web-app







![{\displaystyle \rho =\sum _{i}w_{i}\left[\sum _{j}{\bar {c}}_{ij}(|\alpha _{ij}\rangle \otimes |\beta _{ij}\rangle )\right]\otimes \left[\sum _{k}c_{ik}(\langle \alpha _{ik}|\otimes \langle \beta _{ik}|)\right]}](https://www.marefa.org/api/rest_v1/media/math/render/svg/bf6f2bd84a64fac8cafbb0c06e14180aad4e4401)