احتمال
| الاحتمالات |
|---|
 |
| جزء من سلسلة عن الإحصاء |
| نظرية الاحتمالات |
|---|
 |
In science, the probability of an event is a number that indicates how likely the event is to occur. It is expressed as a number in the range from 0 and 1, or, using percentage notation, in the range from 0% to 100%. The more likely it is that the event will occur, the higher its probability. The probability of an impossible event is 0; that of an event that is certain to occur is 1.[note 1][1][2] The probabilities of two complementary events A and B – either A occurs or B occurs – add up to 1. A simple example is the tossing of a fair (unbiased) coin. If a coin is fair, the two possible outcomes ("heads" and "tails") are equally likely; since these two outcomes are complementary and the probability of "heads" equals the probability of "tails", the probability of each of the two outcomes equals 1/2 (which could also be written as 0.5 or 50%).
These concepts have been given an axiomatic mathematical formalization in probability theory, a branch of mathematics that is used in areas of study such as statistics, mathematics, science, finance, gambling, artificial intelligence, machine learning, computer science and game theory to, for example, draw inferences about the expected frequency of events. Probability theory is also used to describe the underlying mechanics and regularities of complex systems.[3]
Interpretations
When dealing with experiments that are random and well-defined in a purely theoretical setting (like tossing a coin), probabilities can be numerically described by the number of desired outcomes, divided by the total number of all outcomes. For example, tossing a coin twice will yield "head-head", "head-tail", "tail-head", and "tail-tail" outcomes. The probability of getting an outcome of "head-head" is 1 out of 4 outcomes, or, in numerical terms, 1/4, 0.25 or 25%. However, when it comes to practical application, there are two major competing categories of probability interpretations, whose adherents hold different views about the fundamental nature of probability:
- Objectivists assign numbers to describe some objective or physical state of affairs. The most popular version of objective probability is frequentist probability, which claims that the probability of a random event denotes the relative frequency of occurrence of an experiment's outcome when the experiment is repeated indefinitely. This interpretation considers probability to be the relative frequency "in the long run" of outcomes.[4] A modification of this is propensity probability, which interprets probability as the tendency of some experiment to yield a certain outcome, even if it is performed only once.
- Subjectivists assign numbers per subjective probability, that is, as a degree of belief.[5] The degree of belief has been interpreted as "the price at which you would buy or sell a bet that pays 1 unit of utility if E, 0 if not E",[6] although that interpretation is not universally agreed upon.[7] The most popular version of subjective probability is Bayesian probability, which includes expert knowledge as well as experimental data to produce probabilities. The expert knowledge is represented by some (subjective) prior probability distribution. These data are incorporated in a likelihood function. The product of the prior and the likelihood, when normalized, results in a posterior probability distribution that incorporates all the information known to date.[8] By Aumann's agreement theorem, Bayesian agents whose prior beliefs are similar will end up with similar posterior beliefs. However, sufficiently different priors can lead to different conclusions, regardless of how much information the agents share.[9]
Etymology
The word probability derives from the Latin probabilitas, which can also mean "probity", a measure of the authority of a witness in a legal case in Europe, and often correlated with the witness's nobility. In a sense, this differs much from the modern meaning of probability, which in contrast is a measure of the weight of empirical evidence, and is arrived at from inductive reasoning and statistical inference.[10]
History
The scientific study of probability is a modern development of mathematics. Gambling shows that there has been an interest in quantifying the ideas of probability for millennia, but exact mathematical descriptions arose much later. There are reasons for the slow development of the mathematics of probability. Whereas games of chance provided the impetus for the mathematical study of probability, fundamental issues [note 2] are still obscured by the superstitions of gamblers.[11]
According to Richard Jeffrey, "Before the middle of the seventeenth century, the term 'probable' (Latin probabilis) meant approvable, and was applied in that sense, univocally, to opinion and to action. A probable action or opinion was one such as sensible people would undertake or hold, in the circumstances."[12] However, in legal contexts especially, 'probable' could also apply to propositions for which there was good evidence.[13]


The sixteenth-century Italian polymath Gerolamo Cardano demonstrated the efficacy of defining odds as the ratio of favourable to unfavourable outcomes (which implies that the probability of an event is given by the ratio of favourable outcomes to the total number of possible outcomes[14]). Aside from the elementary work by Cardano, the doctrine of probabilities dates to the correspondence of Pierre de Fermat and Blaise Pascal (1654). Christiaan Huygens (1657) gave the earliest known scientific treatment of the subject.[15] Jakob Bernoulli's Ars Conjectandi (posthumous, 1713) and Abraham de Moivre's Doctrine of Chances (1718) treated the subject as a branch of mathematics.[16] See Ian Hacking's The Emergence of Probability[10] and James Franklin's The Science of Conjecture[17] for histories of the early development of the very concept of mathematical probability.
The theory of errors may be traced back to Roger Cotes's Opera Miscellanea (posthumous, 1722), but a memoir prepared by Thomas Simpson in 1755 (printed 1756) first applied the theory to the discussion of errors of observation.[18] The reprint (1757) of this memoir lays down the axioms that positive and negative errors are equally probable, and that certain assignable limits define the range of all errors. Simpson also discusses continuous errors and describes a probability curve.
The first two laws of error that were proposed both originated with Pierre-Simon Laplace. The first law was published in 1774, and stated that the frequency of an error could be expressed as an exponential function of the numerical magnitude of the error—disregarding sign. The second law of error was proposed in 1778 by Laplace, and stated that the frequency of the error is an exponential function of the square of the error.[19] The second law of error is called the normal distribution or the Gauss law. "It is difficult historically to attribute that law to Gauss, who in spite of his well-known precocity had probably not made this discovery before he was two years old."[19]
Daniel Bernoulli (1778) introduced the principle of the maximum product of the probabilities of a system of concurrent errors.
Adrien-Marie Legendre (1805) developed the method of least squares, and introduced it in his Nouvelles méthodes pour la détermination des orbites des comètes (New Methods for Determining the Orbits of Comets).[20] In ignorance of Legendre's contribution, an Irish-American writer, Robert Adrain, editor of "The Analyst" (1808), first deduced the law of facility of error,
where is a constant depending on precision of observation, and is a scale factor ensuring that the area under the curve equals 1. He gave two proofs, the second being essentially the same as John Herschel's (1850).[citation needed] Gauss gave the first proof that seems to have been known in Europe (the third after Adrain's) in 1809. Further proofs were given by Laplace (1810, 1812), Gauss (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), W.F. Donkin (1844, 1856), and Morgan Crofton (1870). Other contributors were Ellis (1844), De Morgan (1864), Glaisher (1872), and Giovanni Schiaparelli (1875). Peters's (1856) formula[مطلوب توضيح] for r, the probable error of a single observation, is well known.
In the nineteenth century, authors on the general theory included Laplace, Sylvestre Lacroix (1816), Littrow (1833), Adolphe Quetelet (1853), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion and Karl Pearson. Augustus De Morgan and George Boole improved the exposition of the theory.
In 1906, Andrey Markov introduced[21] the notion of Markov chains, which played an important role in stochastic processes theory and its applications. The modern theory of probability based on the measure theory was developed by Andrey Kolmogorov in 1931.[22]
On the geometric side, contributors to The Educational Times included Miller, Crofton, McColl, Wolstenholme, Watson, and Artemas Martin.[23] See integral geometry for more information.
Theory
Like other theories, the theory of probability is a representation of its concepts in formal terms—that is, in terms that can be considered separately from their meaning. These formal terms are manipulated by the rules of mathematics and logic, and any results are interpreted or translated back into the problem domain.
There have been at least two successful attempts to formalize probability, namely the Kolmogorov formulation and the Cox formulation. In Kolmogorov's formulation (see also probability space), sets are interpreted as events and probability as a measure on a class of sets. In Cox's theorem, probability is taken as a primitive (i.e., not further analyzed), and the emphasis is on constructing a consistent assignment of probability values to propositions. In both cases, the laws of probability are the same, except for technical details.
There are other methods for quantifying uncertainty, such as the Dempster–Shafer theory or possibility theory, but those are essentially different and not compatible with the usually-understood laws of probability.
Applications
Probability theory is applied in everyday life in risk assessment and modeling. The insurance industry and markets use actuarial science to determine pricing and make trading decisions. Governments apply probabilistic methods in environmental regulation, entitlement analysis, and financial regulation.
An example of the use of probability theory in equity trading is the effect of the perceived probability of any widespread Middle East conflict on oil prices, which have ripple effects in the economy as a whole. An assessment by a commodity trader that a war is more likely can send that commodity's prices up or down, and signals other traders of that opinion. Accordingly, the probabilities are neither assessed independently nor necessarily rationally. The theory of behavioral finance emerged to describe the effect of such groupthink on pricing, on policy, and on peace and conflict.[24]
In addition to financial assessment, probability can be used to analyze trends in biology (e.g., disease spread) as well as ecology (e.g., biological Punnett squares). As with finance, risk assessment can be used as a statistical tool to calculate the likelihood of undesirable events occurring, and can assist with implementing protocols to avoid encountering such circumstances. Probability is used to design games of chance so that casinos can make a guaranteed profit, yet provide payouts to players that are frequent enough to encourage continued play.[25]
Another significant application of probability theory in everyday life is reliability. Many consumer products, such as automobiles and consumer electronics, use reliability theory in product design to reduce the probability of failure. Failure probability may influence a manufacturer's decisions on a product's warranty.[26]
The cache language model and other statistical language models that are used in natural language processing are also examples of applications of probability theory.
Mathematical treatment
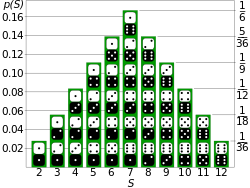
Consider an experiment that can produce a number of results. The collection of all possible results is called the sample space of the experiment, sometimes denoted as . The power set of the sample space is formed by considering all different collections of possible results. For example, rolling a die can produce six possible results. One collection of possible results gives an odd number on the die. Thus, the subset {1,3,5} is an element of the power set of the sample space of dice rolls. These collections are called "events". In this case, {1,3,5} is the event that the die falls on some odd number. If the results that actually occur fall in a given event, the event is said to have occurred.
A probability is a way of assigning every event a value between zero and one, with the requirement that the event made up of all possible results (in our example, the event {1,2,3,4,5,6}) is assigned a value of one. To qualify as a probability, the assignment of values must satisfy the requirement that for any collection of mutually exclusive events (events with no common results, such as the events {1,6}, {3}, and {2,4}), the probability that at least one of the events will occur is given by the sum of the probabilities of all the individual events.[27]
The probability of an event A is written as ,[28] , or .[29] This mathematical definition of probability can extend to infinite sample spaces, and even uncountable sample spaces, using the concept of a measure.
The opposite or complement of an event A is the event [not A] (that is, the event of A not occurring), often denoted as , , or ; its probability is given by P(not A) = 1 − P(A).[30] As an example, the chance of not rolling a six on a six-sided die is 1 – (chance of rolling a six) = 1 − 1/6 = 5/6. For a more comprehensive treatment, see Complementary event.
If two events A and B occur on a single performance of an experiment, this is called the intersection or joint probability of A and B, denoted as
Independent events
If two events, A and B are independent then the joint probability is[28]
For example, if two coins are flipped, then the chance of both being heads is [31]
Mutually exclusive events
If either event A or event B can occur but never both simultaneously, then they are called mutually exclusive events.
If two events are mutually exclusive, then the probability of both occurring is denoted as and
Not mutually exclusive events
If the events are not mutually exclusive then
Conditional probability
Conditional probability is the probability of some event A, given the occurrence of some other event B. Conditional probability is written , and is read "the probability of A, given B". It is defined by[32]
For example, in a bag of 2 red balls and 2 blue balls (4 balls in total), the probability of taking a red ball is however, when taking a second ball, the probability of it being either a red ball or a blue ball depends on the ball previously taken. For example, if a red ball was taken, then the probability of picking a red ball again would be since only 1 red and 2 blue balls would have been remaining. And if a blue ball was taken previously, the probability of taking a red ball will be
Inverse probability
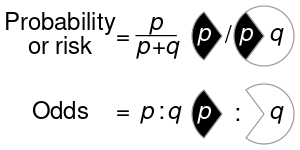
In probability theory and applications, Bayes' rule relates the odds of event to event before (prior to) and after (posterior to) conditioning on another event The odds on to event is simply the ratio of the probabilities of the two events. When arbitrarily many events are of interest, not just two, the rule can be rephrased as posterior is proportional to prior times likelihood, where the proportionality symbol means that the left hand side is proportional to (i.e., equals a constant times) the right hand side as varies, for fixed or given (Lee, 2012; Bertsch McGrayne, 2012). In this form it goes back to Laplace (1774) and to Cournot (1843); see Fienberg (2005). See Inverse probability and Bayes' rule.
Summary of probabilities
| Event | Probability |
|---|---|
| A | |
| not A | |
| A or B | |
| A and B | |
| A given B |
Relation to randomness and probability in quantum mechanics
In a deterministic universe, based on Newtonian concepts, there would be no probability if all conditions were known (Laplace's demon) (but there are situations in which sensitivity to initial conditions exceeds our ability to measure them, i.e. know them). In the case of a roulette wheel, if the force of the hand and the period of that force are known, the number on which the ball will stop would be a certainty (though as a practical matter, this would likely be true only of a roulette wheel that had not been exactly levelled – as Thomas A. Bass' Newtonian Casino revealed). This also assumes knowledge of inertia and friction of the wheel, weight, smoothness, and roundness of the ball, variations in hand speed during the turning, and so forth. A probabilistic description can thus be more useful than Newtonian mechanics for analyzing the pattern of outcomes of repeated rolls of a roulette wheel. Physicists face the same situation in the kinetic theory of gases, where the system, while deterministic in principle, is so complex (with the number of molecules typically the order of magnitude of the Avogadro constant 6.02×1023) that only a statistical description of its properties is feasible.
Probability theory is required to describe quantum phenomena.[34] A revolutionary discovery of early 20th century physics was the random character of all physical processes that occur at sub-atomic scales and are governed by the laws of quantum mechanics. The objective wave function evolves deterministically but, according to the Copenhagen interpretation, it deals with probabilities of observing, the outcome being explained by a wave function collapse when an observation is made. However, the loss of determinism for the sake of instrumentalism did not meet with universal approval. Albert Einstein famously remarked in a letter to Max Born: "I am convinced that God does not play dice".[35] Like Einstein, Erwin Schrödinger, who discovered the wave function, believed quantum mechanics is a statistical approximation of an underlying deterministic reality.[36] In some modern interpretations of the statistical mechanics of measurement, quantum decoherence is invoked to account for the appearance of subjectively probabilistic experimental outcomes.
See also
- In law
Notes
- ^ The converse is not necessarily true. Strictly speaking, a probability of 0 indicates that an event almost never takes place, whereas a probability of 1 indicates than an event almost certainly takes place. This is an important distinction when the sample space is infinite. For example, for the continuous uniform distribution on the real interval [5, 10], there are an infinite number of possible outcomes, and the probability of any given outcome being observed — for instance, exactly 7 — is 0. This means that when we make an observation, it will almost surely not be exactly 7. However, it does not mean that exactly 7 is impossible. Ultimately some specific outcome (with probability 0) will be observed, and one possibility for that specific outcome is exactly 7.
- ^ In the context of the book that this is quoted from, it is the theory of probability and the logic behind it that governs the phenomena of such things compared to rash predictions that rely on pure luck or mythological arguments such as gods of luck helping the winner of the game.
References
- ^ "Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th Ed, (2009), ISBN 978-0-534-24312-8.
- ^ William Feller, An Introduction to Probability Theory and Its Applications, (Vol 1), 3rd Ed, (1968), Wiley, ISBN 0-471-25708-7.
- ^ Probability Theory The Britannica website
- ^ Hacking, Ian (1965). The Logic of Statistical Inference. Cambridge University Press. ISBN 978-0-521-05165-1.[صفحة مطلوبة]
- ^ Finetti, Bruno de (1970). "Logical foundations and measurement of subjective probability". Acta Psychologica. 34: 129–145. doi:10.1016/0001-6918(70)90012-0.
- ^ Hájek, Alan (21 أكتوبر 2002). Edward N. Zalta (ed.). "Interpretations of Probability". The Stanford Encyclopedia of Philosophy (Winter 2012 ed.). Retrieved 22 أبريل 2013.
- ^ Jaynes, E.T. (2003). "Section A.2 The de Finetti system of probability". In Bretthorst, G. Larry (ed.). Probability Theory: The Logic of Science (in الإنجليزية) (1 ed.). Cambridge University Press. ISBN 978-0-521-59271-0.
- ^ Hogg, Robert V.; Craig, Allen; McKean, Joseph W. (2004). Introduction to Mathematical Statistics (6th ed.). Upper Saddle River: Pearson. ISBN 978-0-13-008507-8.[صفحة مطلوبة]
- ^ Jaynes, E.T. (2003). "Section 5.3 Converging and diverging views". In Bretthorst, G. Larry (ed.). Probability Theory: The Logic of Science (in الإنجليزية) (1 ed.). Cambridge University Press. ISBN 978-0-521-59271-0.
- ^ أ ب Hacking, I. (2006) The Emergence of Probability: A Philosophical Study of Early Ideas about Probability, Induction and Statistical Inference, Cambridge University Press, ISBN 978-0-521-68557-3[صفحة مطلوبة]
- ^ Freund, John. (1973) Introduction to Probability. Dickenson ISBN 978-0-8221-0078-2 (p. 1)
- ^ Jeffrey, R.C., Probability and the Art of Judgment, Cambridge University Press. (1992). pp. 54–55 . ISBN 0-521-39459-7
- ^ Franklin, J. (2001) The Science of Conjecture: Evidence and Probability Before Pascal, Johns Hopkins University Press. (pp. 22, 113, 127)
- ^ "Some laws and problems in classical probability and how Cardano anticipated them Gorrochum, P. Chance magazine 2012" (PDF).
- ^ Abrams, William, A Brief History of Probability, Second Moment, http://www.secondmoment.org/articles/probability.php, retrieved on 2008-05-23
- ^ Ivancevic, Vladimir G.; Ivancevic, Tijana T. (2008). Quantum leap : from Dirac and Feynman, across the universe, to human body and mind. Singapore ; Hackensack, NJ: World Scientific. p. 16. ISBN 978-981-281-927-7.
- ^ Franklin, James (2001). The Science of Conjecture: Evidence and Probability Before Pascal. Johns Hopkins University Press. ISBN 978-0-8018-6569-5.
- ^ Shoesmith, Eddie (نوفمبر 1985). "Thomas Simpson and the arithmetic mean". Historia Mathematica (in الإنجليزية). 12 (4): 352–355. doi:10.1016/0315-0860(85)90044-8.
- ^ أ ب Wilson EB (1923) "First and second laws of error". Journal of the American Statistical Association, 18, 143
- ^ Seneta, Eugene William. ""Adrien-Marie Legendre" (version 9)". StatProb: The Encyclopedia Sponsored by Statistics and Probability Societies. Archived from the original on 3 فبراير 2016. Retrieved 27 يناير 2016.
- ^ Weber, Richard. "Markov Chains" (PDF). Statistical Laboratory. University of Cambridge.
- ^ Vitanyi, Paul M.B. (1988). "Andrei Nikolaevich Kolmogorov". CWI Quarterly (1): 3–18. Retrieved 27 يناير 2016.
- ^ Wilcox, Rand R. (10 مايو 2016). Understanding and applying basic statistical methods using R. Hoboken, New Jersey. ISBN 978-1-119-06140-3. OCLC 949759319.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Singh, Laurie (2010) "Whither Efficient Markets? Efficient Market Theory and Behavioral Finance". The Finance Professionals' Post, 2010.
- ^ Gao, J.Z.; Fong, D.; Liu, X. (أبريل 2011). "Mathematical analyses of casino rebate systems for VIP gambling". International Gambling Studies. 11 (1): 93–106. doi:10.1080/14459795.2011.552575. S2CID 144540412.
- ^ Gorman, Michael F. (2010). "Management Insights". Management Science. 56: iv–vii. doi:10.1287/mnsc.1090.1132.
- ^ Ross, Sheldon M. (2010). A First course in Probability (8th ed.). Pearson Prentice Hall. pp. 26–27. ISBN 9780136033134.
- ^ أ ب Weisstein, Eric W. "Probability". mathworld.wolfram.com (in الإنجليزية). Retrieved 10 سبتمبر 2020.
- ^ Olofsson (2005) p. 8.
- ^ Olofsson (2005), p. 9
- ^ Olofsson (2005) p. 35.
- ^ Olofsson (2005) p. 29.
- ^ "Conditional probability with respect to a sigma-algebra". www.statlect.com. Retrieved 4 يوليو 2022.
- ^ Burgin, Mark (2010). "Interpretations of Negative Probabilities". p. 1. arXiv:1008.1287v1 [physics.data-an].
- ^ Jedenfalls bin ich überzeugt, daß der Alte nicht würfelt. Letter to Max Born, 4 December 1926, in: Einstein/Born Briefwechsel 1916–1955.
- ^ Moore, W.J. (1992). Schrödinger: Life and Thought. Cambridge University Press. p. 479. ISBN 978-0-521-43767-7.
Bibliography
- Kallenberg, O. (2005) Probabilistic Symmetries and Invariance Principles. Springer-Verlag, New York. 510 pp. ISBN 0-387-25115-4
- Kallenberg, O. (2002) Foundations of Modern Probability, 2nd ed. Springer Series in Statistics. 650 pp. ISBN 0-387-95313-2
- Olofsson, Peter (2005) Probability, Statistics, and Stochastic Processes, Wiley-Interscience. 504 pp ISBN 0-471-67969-0.
وصلات خارجية
| مراجع مكتبية عن Probability |
- Virtual Laboratories in Probability and Statistics (Univ. of Ala.-Huntsville)
- Probability on In Our Time at the BBC. (/In_Our_Time_Probability listen now)
- Probability and Statistics EBook
- Edwin Thompson Jaynes. Probability Theory: The Logic of Science. Preprint: Washington University, (1996). — HTML index with links to PostScript files and PDF (first three chapters)
- People from the History of Probability and Statistics (Univ. of Southampton)
- Probability and Statistics on the Earliest Uses Pages (Univ. of Southampton)
- Earliest Uses of Symbols in Probability and Statistics on Earliest Uses of Various Mathematical Symbols
- A tutorial on probability and Bayes' theorem devised for first-year Oxford University students
- [1] pdf file of An Anthology of Chance Operations (1963) at UbuWeb
- Introduction to Probability – eBook Archived 27 يوليو 2011 at the Wayback Machine, by Charles Grinstead, Laurie Snell Source Archived 25 مارس 2012 at the Wayback Machine (GNU Free Documentation License)
- (in إنگليزية and إيطالية) Bruno de Finetti, Probabilità e induzione, Bologna, CLUEB, 1993. ISBN 88-8091-176-7 (digital version)
- Richard Feynman's Lecture on probability.
- مقالات بالمعرفة بحاجة لذكر رقم الصفحة بالمصدر from June 2012
- CS1 maint: location missing publisher
- Short description is different from Wikidata
- Articles with hatnote templates targeting a nonexistent page
- Use dmy dates from October 2013
- Articles containing لاتينية-language text
- Lang and lang-xx code promoted to ISO 639-1
- Articles with unsourced statements from June 2012
- جميع الصفحات التي تحتاج تنظيف
- مقالات بالمعرفة تحتاج توضيح from June 2012
- Articles with إنگليزية-language sources (en)
- Articles with إيطالية-language sources (it)
- Probability
- أعداد لابعدية
- رياضيات
- احتمالات



































![{\displaystyle P(A)\in [0,1]}](https://www.marefa.org/api/rest_v1/media/math/render/svg/8f07aab47c06682ab4a8b4934f5db8c813e3eff6)





