نظرية النسبية العامة
| جزء من سلسلة عن |
| علم الكون الطبيعي |
|---|
 |

| النسبية العامة |
|---|
 |
النظرية النسبية العامّة هي نظرية نشرها ألبرت أينشتاين في عام 1915. وهي تمثل الوصف الحالي للجاذبية في الفيزياء الحديثة. كما أنها تعميم للنظرية النسبية الخاصة حيث توحد بين النسبية الخاصة وقانون نيوتن للجاذبية، وتصف الجاذبية كخاصة لهندسة المكان والزمان، أو ما يعرف بالزمكان.
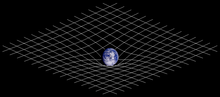
وأضافت النظرية النسبية العامة فكرة تقعر الفراغ بوجود المادة، وهو الأمر الذي يعني أن الخطوط المستقيمة تتشوه بوجود الكتلة، وأثبتت النظرية النسبية العامة عندما تحقق تنبؤ أينشتاين بالتباعد الظاهري لنجمين في فترة كسوف الشمس وذلك يعود إلى تشوه مسار الضوء القادم من النجمين بسبب مرورهما قرب الشمس ذات الكتلة العالية نسبيا وبالتالي تقوس خط سير الضوء القادم من النجمين.
تاريخ النسبية العامة
بعد وقت قصير من نشره للنظرية النسبية الخاصة في عام 1905، بدأ أينشتاين التفكير في كيفية دمج الجاذبية بالنسبية في إطار جديد. في عام 1907، بدأ في تجربة فكرية بسيطة تشمل مراقبة سقوط حر واستمر البحث لمدة ثماني سنوات للوصول إلى نظرية نسبية بالجاذبية. بعد العديد من الطرق الالتفافية وبدايات خاطئة، بلغ عمله ذروته في تشرين الثاني 1915 حيث عرض في الأكاديمية البروسية للعلوم ما يعرف الآن باسم معادلات أينشتاين للمجال. هذه المعادلات تحددتتأثير هندسة المكان والزمن على أي مادة، وتشكل هذه المعادلات جوهر نظرية أينشتاين في النسبية العامة.[1]
إن معادلات أينشتاين للمجال هي معادلات غير خطية ومن الصعب حلها. وقد استخدم إنشتاين طريقة تقريبة للخروج بالنتيجة التي تنبأ فيها. في بداية عام 1916 وجد عالم الفلك كارل شوارتسشيلد الحل التام لمعادلات إينشتاين ودعيت مترية شوارزشيلد. وهذه الحلول وضعت الحل لوصف المراحل الأخيرة من انهيار الجاذبية، والأجسام التي تعرف اليوم ثقوب سوداء. وكانت الخطوة الأولى في تعميم شوارزشيلد في حلول الأجسام المشحونة كهربائيا وفي النهاية أسفرت عن مترية ريسنر- نوردستوورم. وهي حاليا مرتبطة بشحنة الثقب الأسود.[2]
طبق أينشتاين في سنة 1917 نظريته على الكون ككل، والشروع في النسبية الكونية. وكان قد فرض تماشيا مع الفكر السائد أن الكون ساكن وأضاف بارمتر جديد إلى معادلات المجال وهو الثابت الكوني.[3] أدت حلول ألكسندر فريدمان إلى فكرة تمدد الكون سنة 1922 عن طريق الاستغناء عن الثابت الكوني والتي أيدت فيما بعد بواسطة مراقبات إدوين هابل وآخرين. واستخدم جورجيوس ليمرت هذه الحلول ليصيغ أول شكل من تظرية الإنفجار العظيم من أن الكون تطور من حالة بدائية مفرطة في السخونة والكثافة.[4] إعترف أنيشتاين فيما بعد بأن اعتباره بأن الكون ثابت كان أكبر خطأ ارتكبه في حياته.[5]
خلال تلك الفترة بقيت النظرية النسبية العامة كنوع من الفضول في مواضيع النظريات فيزيائية، وبقي واضحا تفوق قانون الجذب العام لنيوتن، والتي بدت منسجمة مع النسبية الخاصة الي استخدم في العديد من الحالات التي يمكن شرحها من خلال قانون نيوتن.
محطات في تاريخ النظرية
هناك محطات مثلت نقاطاً فارقة في تطوّر نظرية النسبية العامة، سواء لجهة إثباتها أو نفيها. ومن بينها، تبرز المحطّات التالية:
- الحرب العالمية الأولى: ظهرت نظرية أينشتاين في ظروف تلك الحرب. وعلى خطوط الجبهة الألمانية - الروسية، لم تحل المعارك دون انشغال عالِم الفيزياء الألماني كارل شوارتزشايلد، بنظريّة النسبيّة. وتوصّل إلى رسم صورة كونيّة لمركّب الزمان - المكان تجعله على هيئة كرة متناسقة ومستقرة، لكنها هائلة الأبعاد. وفي المقلب الآخر، عمل عالم الفلك البريطاني آرثر إيدنغتون مع زميله رويال دايسون، على رصد مواقع النجوم أثناء كسوف شمسي كامل، وقارنها مع مواقعها في الليل. وأثبتا أن هناك فارقاً، ما يعني أن الشمس وجاذبيتها تؤثران في الضوء الآتي من النجوم إلى الأرض، وهو جزء أساسي من نظرية أينشتاين.
- 1915: ما كادت نظرية أينشتاين تظهر، حتى جاءها تأييد غير متوقع من كوكب «عطارد» القريب من الشمس. وطوال عشرات السنوات، لم يتمكن العلماء من فهم مسار «عطارد» بالاستناد إلى المعادلات الشهيرة التي وضعها العالِم إسحاق نيوتن عن الجاذبيّة. وفي العام 1859، لاحظ عالم الفلك أوربيان لو فيربيار، أن مدار «عطارد» هو أكثر دقّة مما تفترضه معادلات نيوتن. وطبّق آينشتاين معادلات النسبيّة العامة على مدار «عطارد»، فأعطت تفسيراً للدقّة الصارمة التي يتميّز بها ذلك المسار!
- 1935: اندلاع معركة الثقب الأسود. لم يملك الشاب الهندي سوبراهمانيان شاندراساخير، مالاً ليحجز ولو مجرد سرير على السفينة التي حملته إلى بريطانيا. وصرف ذلك العالِم وقته جالساً على كرسي، ومنكباً على أوراق دوّن عليها معادلات فيزياء من وحي نظرية آينشتاين، وبعضاً من معادلات الفيزياء الكمومية. وقبيل وصوله إلى بريطانيا، توصّل إلى أن بعض النجوم الضخمة ينطفئ، ليتحوّل إلى «ثقب أسود»، لديه قوة جاذبيّة هائلة. وتعارض ذلك مع النظريات التي كانت سائدة في جامعة كامبردج، حيث عرض شاندراساخير نظريته في العام 1935. ولم يلقّ سوى السخرية والازدراء. فسافر إلى أميركا. ودرّس في جامعاتها. واعتبر أبرز شارح لنظرية آينشتاين. وتدريجاً، تقبّل العلماء نظرية «الثقب الأسود». وفي 1983، نال شاندراساخير جائزة نوبل عن تلك النظرية. وفي 1999، كرّمته وكالة ناسا بأن أطلقت اسم «شاندرا» على أول تلسكوب فضائي يرصد الكون باستخدام أشعة إكس.
- 1936: أينشتاين يتعمد تحاشي تدقيق العلماء! نالت الشهرة قليلاً من آينشتاين، إذ أعطته بعضاً من العناد، ما أوقعه في الخطأ. ففي تلك السنة، قدّم آينشتاين مقالاً إلى مجلة علمية موثوقة، عن موجات الجاذبيّة، يؤكّد عدم وجودها. وقدّمت المجلة المقال إلى علماء فيزياء كي يراجعوه. وثارت حفيظة آينشتاين، فسحب المقال من المجلة. ولعب الحظّ إلى جانبه. إذ أعطى المقال إلى مجلة علميّة أخرى، بعد فترة وجيزة. وقبل وصوله إلى الطباعة، راجع آينشتاين مقاله، ووجد أنه أخطأ في شأن موجات الجاذبية. وأعاد صياغة المقال، مسلّماً بإمكان وجود تلك الموجات. وكرّرت المجلة الثانية ما فعلته نظيرتها الأولى، فأعطت مقال آينشتاين إلى عالِم ليراجعه، تبيّن لاحقاً أنه العالِم هاورد روبرتسون. وعلى رغم نشر المقال، إلا أن روبرتسون لاحظ «اهتزازاً» علميّاً فيه. وبعد فترة، استطاع روبرتسون بكياسة إقناع صديقه آينشتاين بأنه ارتكب خطأً علميّاً.
- 1959: إثبات أن الجاذبيّة تبطئ الزمن. في تجربة لروبرت باوند وغلين ريبيكا، وهما عالِما فيزياء في «جامعة هارفرد»، ثبت أن ضوء الشمس الذي هو مقياس الوقت، يتباطأ قليلاً عند دخوله حقل جاذبيّة الأرض. وفي العام 1977، عندما صُنِع نظام الـ «جي بي إس»، أدخل العلماء ذلك التباطؤ ضمن معادلاتهم، ما ضمن دقة التزامن في حساب الموجات الكهرومغناطيسيّة (وهي تسير بسرعة الضوء)، بين الأقمار الاصطناعيّة في الفضاء الخارجي الضعيف الجاذبيّة، ومستخدمي نظام «جي بي أس» على الأرض.[6]
- 1974: نجوم تبرهن عن وجود موجات الجاذبيّة. في ذلك العام، راقب جوزيف تايلور وراسل هولز، وكلاهما اختصاصي في علم فيزياء الفلك، بعض النجوم المنهارة. واستخدما قرصاً راداريّاً قطره 305 أمتار، كي يلاحقا الطاقة التي تصدر من تلك النجوم. ولاحظ العالمان بعد متابعة امتدت سنوات طويلة، أن تلك الطاقة تخرج في «نبضات» غير منتظمة، إضافة إلى حدوث تقلّص تدريجي في مدار النجوم. وتوافقت تلك الملاحظات مع نظرية آينشتاين، كما أضافت تأكيداً عن وجود موجات للجاذبيّة وأنّها السبب في عدم انتظام «نبضات» الطاقة الصادرة عن النجوم المنهارة. وفي 1993، نال جوزيف تايلور وراسل هولز، جائزة نوبل عن ذلك العمل.
من الميكانيكا الكلاسيكية إلى النسبية العامة
إن أفضل طريقة لفهم النسبية العامة من خلال معرفة التشابه والاختلاف بينها وبين الفيزياء الكلاسيكية. الخطوة الأولى هي إدراك أن الميكانيكا الكلاسيكية وقانون نيوتن للجذب هو ضمن الهندسة الوصفية, والجمع بين هذه القوانين والنسبية الخاصة ستساعد على اشتقاق النسبية العامة..[7]
هندسة الجاذبية النيوتونية
حسب قواعد الميكانيك الكلاسيكي فإن حركة الجسم توصف بدرجات بأنها مكونة من حركة حرة (أو حركة مقصورة)، ومقدار انحرافه عن هذه الحركة الحرة. فعلى سبيل المثال القوى الخارجية المطبقة على جسم متحرك وفق قانون نيوتن الثاني والذي ينص على أن مجموع القوى الخارجية بشكل شعاعي المطبقة على جسم يساوي إلى جداء كتلة (عطالة)الجسم بالقيمة الشعاعية للتسارع.[8] ترتبط الحركة المقصورة بهندسة الزمان و المكان. ففي الإطار المرجعي التقليدي للميكانيكا الكلاسيكية فإن الجسم ذو الحركة الحرة يتحرك على طول خط مستقيم وفق سرعة ثابتة. أما وفق المصطلح الحديث فإن المسار هو مسار جيوديسي فهو خطوط مستقيمة ضمن فضاء منحني.[9]
مبدأ التكافؤ في النسبية العامة
نميز في الفيزياء بين مراجع عطالية (جمل مرجعية عطالية inertial reference systems) و مراجع غير عطالية non-inertial ، حيث يمكن لأي جسم أن يحافظ على حركته المنتظمة في الجمل العطالية ما لم يخضع لقوة ما أو يتأثر بجسم آخر ضمن نفس الجملة ، في حين تكتسب الأجسام في الجمل غير العطالية تسارعا ناجما عن حركة الجملة نفسها و تسارعها و ليس نتيجة تأثير جسم داخلي ضمن الجملة . تتم تفسير مقاومة هذا التسارع بقوى افتراضية ندعوها قوى العطالة inertial forces في حالة الحركة المتقيمة للجمل المرجعية او قوى العطالة النابذة في حالة الحركة الدورانية rotational movement للجمل المرجعية . هذه القوى تعتبر قوى افتراضية غير فيزيائية في الميكانيك الكلاسيكي النيوتني لكن في النسبية العامة ليس هناك مجالا لمثل هذا التمييز حسب مبدأ التكافؤ (اقرأ تجربة المصعدين الفكرية في صفحة مبدأ التكافؤ ) .
وليس هناك من قوة ثقالية ضمن الاطار المرجعي في حالة السقوط الحر ( الحركة المتسارعة ) عدا القوى المدية للثقالة التي تشوه الأجسام دون التأثير على حركتها و سرعتها ( دون تسارع ). و حتى محاولات الكشف عن الأموج الثقالية تعتمد على هذه القوى المدية(tidal forces) .
و قد استند اينشتاين في الواقع على حقيقة معروفة منذ غاليليو ألا وهي تماثل الكتلتين الثقالية و العطالية للأجسام ، مما يؤكد ان التسارع الحركي و الثقالة(gravity)هي مظاهر لأمر واحد . و يفترض أنه لا وجود لأي تجربة يمكن ان تميز بين حقل ثقالي-جاذبية-و تسارع منتظم . و سرعان ما وسع اينشتاين مبدأ التكافؤ في نظريته ليشمل مفهوما اضافيا هو استحالة تحديد حالة الحركة لجملة مرجعية غير متسارعة عن طريق أي قياس فيزيائي . و على هذا فلا يمكن ايجاد أي تغير في الثوابت الفيزيائية الاساسية مثل كتلة الراحة أو الشحن الكهربائية للجسيمات الأولية ، والا فان اي تغير في هذه الثوابت يطعن في صحة النسبية العامة . يذكر ان النظرية النسبية هي أحد أهم النظريات في العلم الحديث .
النتائج الهندسية
بالرغم من الاهتمام الأساسي في الهندسة كان منصبا لفترة طويلة على القواعد في الفضاء الاقليدي فيما يعرف بالهندسة الاقليدية فقد قام عدد من علماء الرياضيات بصياغة هندسات لااقليدية مثل لوباتشوفسكي و ريمان و غاوس و غيرهم . لكن التصور الاساسي للفضاء بقي اقليديا طيلة قرون لتوافقه مع معظم النظريات الفيزيئية بخاصة ميكانيك نيوتن . لكن ظهور النسبية العامة فتح الباب للاعتقاد حول لااقليدية الزمكان(الزمان + المكان = الزمكان ) و قد أكدت الكثير من التجارب هذه الحقيقة .
الأمواج الثقالية
يعتبر التنبؤ بالأمواج الثقالية احدى أهم النتائج والبراهين على النسبية العامة . و لتبسيط الموضوع يمكننا تشبيه القوة الثقالية بالقوة الكهربائية : حيث تقابل الكتلة Mass في الثقالة الشحنة charge في القوة الكهربائية . و أي اضطراب في هذه الشحنات يحدث في الجوار أمواجا كهرمغناطيسية تنتشر بسرعة تساوي سرعة الضوء ، بشكل مماثل يحدث اضطراب الأجسام ذات الكتل الضخمة نشوء أمواج تنتشر في حقل الثقالة المحيط بها, لكن أمواج الثقالة خلافا للأمواج الكهرمغناطيسية هي اضطراب يطرأ على الفضاء نفسه ( نتذكر أن الثقالة في النسبية هي تعبير عن تشوه الزمكان نفسه ) وهكذا تبدو أمواج الثقالة كاضطراب زمكاني ينتشر بعيدا عن موقع الاضطراب .
انظر أيضا
- تجربة يوتڤوس
- المساهمون في النسبية العامة
- عمل أينشتاين-هيلبرت
- النسبية الخاصة
- معادلات آينشتاين للمجال
- نظرية أينشتاين-كارتان
- زمكان
المصادر
- موجز تاريخ الزمن : Brief History of time < Stephen Hawking
- الأمواج الثقالية : Gravitational waves ، Kip Thorn
- الكون الأنيق : Elegant Cosmos ، Briane Greene
- ^ This development is traced in chapters 9 through 15 of Pais 1982 and in Janssen 2005; an up-to-date collection of current research, including reprints of many of the original articles, is Renn 2007; an accessible overview can be found in Renn 2005, p. 110ff.. An early key article is Einstein 1907, cf. Pais 1982, ch. 9. The publication featuring the field equations is Einstein 1915, cf. Pais 1982, ch. 11–15.
- ^ See Schwarzschild 1916a, Schwarzschild 1916b and Reissner 1916 (later complemented in Nordström 1918).
- ^ Einstein 1917, cf. Pais 1982, ch. 15e.
- ^ Hubble's original article is Hubble 1929; an accessible overview is given in Singh 2004, ch. 2–4.
- ^ As reported in Gamow 1970. Einstein's condemnation would prove to be premature, cf. the sectionCosmology, below.
- ^ "6 محطات في تاريخ النسبيّة العامة". جريدة الحياة اللبنانية. 2015-11-03. Retrieved 2015-11-03.
- ^ The following exposition re-traces that of Ehlers 1973, section 1.
- ^ See, for instance, Arnold 1989, chapter 1.
- ^ See Ehlers 1973, pp. 5f..