ميكانيكا لاگرانج
| ميكانيكا كلاسيكية | ||||||||
تاريخ...
| ||||||||
ميكانيكا لاگرانج أو ميكانيكا لاجرانج Lagrangian mechanics عبارة عن إعادة صياغة للمكيانيك الكلاسيكي قدمه جوزيف لويس لاغرانج عام 1788. في ميكانيك لاغرانج ، مسار الجسم يشتق بإيجاد المسلك الذي يقلل الفعل action ، و هو مقدار يعتبر تكامل لكمية ندعوها لاغرانجي Lagrangian على الزمن . اللاغرانجي بالنسبة للميكانيك الكلاسيكي يعتبر الفرق بين الطاقة الحركية و الطاقة الكامنة .
هذا الموضوع يبسط بصورة كبيرة الكثير من المسائل الفيزيائية . مثلا كرة صغيرة في حلقة . إذا قمنا بالحساب على أساس الميكانيك النيوتني ، سيحصل المرء على مجموعة معقدة من المعادلات التي ستأخذ بعين الاعتبار القوى التي تؤثر بها الدوامة على الكرية في كل لحظة .
نفس هذه المسألة تصبح أسها باستخدام ميكانيك لاغرانج . حيث ينظر المرء إلى جميع الحركات الممكنة التي تقوم بها الكرية على الدوامة و يجد رياضيا الحركة التي تقلل الفعل إلى ادنى حد . بالتالي يكون لدينا عدد أقل من المعادلات لأنها لا تمثل حسابا مباشرا لتأثير الدوامة على الكرية عند كل لحظة .
معادلات لاگرانج
لنعتبر جسيما مفردا ذو كتلة m و شعاع موضع r . تطبق عليه قوة F ، يمكن عندئذ أن نعبر عن هذه القوة على أنها تدرج تابع الطاقة الكامنة القياسي (V(r, t:
مثل هذه القوة تكون مستقلة عن المشتق الثالث أو المشتقات الأعلى رتبة لشعاع الموضع r ، لذا فإن هذه قانون نيوتن الثاني يشكل مجموعة من ثلاث معادلات تفاضلية نظامية من الرتبة الثانية .
لذا فإن حركة هذا الجسيم يمكن وصفها بدلالة متغيرات مستقلة أو ما يدعى " درجات حرية " . درجات الحرية هذه هي مجموعمة من ستة متغيرات :
{ rj, r′j | j = 1, 2, 3},
المركبات الديكارتية لشعاع الموضع r و مشتقاته الزمنية ( مشتقاته بالنسبة للزمن ), في لحظة زمنية معينة أي أن الموضع (x,y,z) و السرعة بمكوناتها الديكارتية الثلاثة :
((vx,vy,vz ) ).
بشكل أعم ، يمكننا العمل ضمن جملة إحداثيات معممة
, qj, مع مشتقاتها الزمنية ، أو ما يدعى بالسرع معممة ، q′j.
يرتبط شعاع الموضع r مع الإحداثيات المعممة عن طريق جملة معادلات تحويل
فمثلا من أجل نواس بسيط ذو طول l ، يكون الخيار المنطقي للإحداثيات المعممة هو زاوية النواس التي يصنعها مع خطه الشاقولي ( العمودي ) ، θ,
و تكون معادلات التحويل :
- .
مصطلح إحداثيات معممة أحد بقايا فترة استخدام الإحداثيات الديكارتية كنظام إحداثيات افتراضي .
لنعتبر الإزاحة الإعتبارية للجسم δr فيكون العمل المنجز من قبل القوة F هو :
δW = F · δr.
باستخدام قانون نيوتن الثاني يمكننا أن نكتب :
بما أن العمل كمية فيزيائية قياسية ( كمية و ليست شعاعية ) يمكننا إعادة كتابة هذه المعادلات بدلالة الإحداثيات المعممة و السرع على الجانب الأيسر .
عملية تنسيق الجانب الأيمن أكثر صعوبة لكن بعد الترتيب و التبديل :
حيث هي الطاقة الحركية للجسيم T = 1/2 m r′ 2 . و معادلة العمل المنجز ستصبح بالشكل :
على أي حال ، فإن هذا يجب أن يكون صحيحا بالنسبة لأي مجموعة من الإزاحات المعممة δqi, لذا يكون لدينا :
من أجل أي من الإحداثيات المعممة δqi.
يمكننا أن نبسط هذه المعادلة بملاحظة V أن هو تابع ل r و t, و شعاع الموضع r تابع أيضا للإحداثيات المعممة و الزمن t لذا فإن السرعة V تكون مستقلة عن السرع المعممة
بإدخال هذا في المعادلة السابقة و استبدال L = T - V نحصل على معادلات لاگرانج :
هناك دوما معادلة لاگرانج وحيدة لكل إحداثي معمم qi. و عندما يكون
qi = ri (أي أن الإحداثيات المعممة هي ببساطة إحداثيات ديكارتية ), عندئذ نستطيع بسهولة اختزال معادلة لاغرانج إلى قانون نيوتن الثاني.
الاشتقاق أعلاه يمكن تعميمه على نظام (جملة) مؤلفة من N جسيم. عندئذ يكون هناك 6N إحداثي معمم يرتبطان بإحداثيات الموضع عن طريق معادلات التحويل الثلاثية 3N . في معادلات لاغرانج 3N يكون دوما T هو الطاقة الحركية الكلية للجملة ، و V الطاقة الكامنة الكلية .
عمليا من الأسهل حل المسألة ياستخدام معادلة اويلر-لاگرانج بدلا من قوانين نيوتن . ذلك لأن الإحداثيات المعممة qi يمكن اختيارها لتلائم تناظرات النظام .
كتلة ساقطة
- .
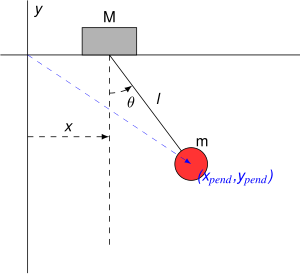
بندول على دعامة قابلة للحركة
and the potential energy of the system is
اللاگرانجي يصبح:
Now carrying out the differentiations gives for the support coordinate x
therefore:
indicating the presence of a constant of motion. The other variable yields
- ;
therefore
- .
مبدأ هاملتون
العمل، ذو الرمز ، هو التكامل الزمني للاگرانجي:
Let q0 and q1 be the coordinates at respective initial and final times t0 and t1. Using the calculus of variations, it can be shown the Lagrange's equations are equivalent to Hamilton's principle:
- The system undergoes the trajectory between t0 and t1 whose action has a stationary value.
By stationary, we mean that the action does not vary to first-order for infinitesimal deformations of the trajectory, with the end-points (q0, t0) and (q1,t1) fixed. Hamilton's principle can be written as:
Thus, instead of thinking about particles accelerating in response to applied forces, one might think of them picking out the path with a stationary action.
في عام 1948، اخترع ريتشارد فاينمان صياغة تكامل المسار ممدداً مبدأ أقل عمل إلى ميكانيكا الكم للإلكترونات و الفوتونات. In this formulation, particles travel every possible path between the initial and final states; the probability of a specific final state is obtained by summing over all possible trajectories leading to it. In the classical regime, the path integral formulation cleanly reproduces Hamilton's principle, and Fermat's principle in optics.
انظر أيضاً
- Canonical coordinates
- Functional derivative
- Generalized coordinates
- ميكانيكا هاملتونية
- Lagrangian analysis (applications of Lagrangian mechanics)
- Nielsen form
- Restricted three-body problem
المصادر
- Goldstein, H. Classical Mechanics, second edition, pp.16 (Addison-Wesley, 1980)
- Moon, F. C. Applied Dynamics With Applications to Multibody and Mechatronic Systems, pp. 103-168 (Wiley, 1998).
قراءات اضافية
- Landau, L.D. and Lifshitz, E.M. Mechanics, Pergamon Press.
- Gupta, Kiran Chandra, Classical mechanics of particles and rigid bodies (Wiley, 1988).
وصلات خارجية
- Tong, David, Classical Dynamics Cambridge lecture notes
- Principle of least action interactive Excellent interactive explanation/webpage
- Aerospace dynamics lecture notes on Lagrangian mechanics
- Aerospace dynamics lecture notes on Rayleigh dissipation function
- Introduction to Lagrangian Mechanics [1]
- [2] Sydney Grammar School Academic Extension notes






![{\displaystyle m\mathbf {r''} \cdot \delta \mathbf {r} =\sum _{i}\left[{d \over dt}{\partial T \over \partial q'_{i}}-{\partial T \over \partial q_{i}}\right]\delta q_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5e740779aa0bfc9a87df7074b534c3b0f3743b6)
![{\displaystyle \sum _{i}\left[{d \over dt}{\partial {T} \over \partial {q'_{i}}}-{\partial {(T-V)} \over \partial q_{i}}\right]\delta q_{i}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b35be1e6877c56a2146e3725706856dbc25b923e)
![{\displaystyle \left[{d \over dt}{\partial {T} \over \partial {q'_{i}}}-{\partial {(T-V)} \over \partial q_{i}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/955e60ddee0c8789a3d7e1f1a75c2bbc98735c16)



![{\displaystyle T={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left({\dot {x}}_{\mathrm {pend} }^{2}+{\dot {y}}_{\mathrm {pend} }^{2}\right)={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+l{\dot {\theta }}\cos \theta \right)^{2}+\left(l{\dot {\theta }}\sin \theta \right)^{2}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16c68827d12988d5dd72420763cd6f75f1e00ade)

![{\displaystyle {\mathcal {L}}=T-V={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+l{\dot {\theta }}\cos \theta \right)^{2}+\left(l{\dot {\theta }}\sin \theta \right)^{2}\right]+mgl\cos \theta ={\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}+m{\dot {x}}l{\dot {\theta }}\cos \theta +{\frac {1}{2}}ml^{2}{\dot {\theta }}^{2}+mgl\cos \theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3f0d788e449dc61ac51fc07aedca8e679643893)
![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left[(M+m){\dot {x}}+ml{\dot {\theta }}\cos \theta \right]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f4dc10c5efff1bb5cd67fa3fbe797f40177619)

![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left[m({\dot {x}}l\cos \theta +l^{2}{\dot {\theta }})\right]+m({\dot {x}}l{\dot {\theta }}+gl)\sin \theta =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c31d974aa878c620dad3ebb566dfc0672f07d45)



