قانون الجذب العام لنيوتن

ميكانيكا كلاسيكية

${\displaystyle{\displaystyle{\vec{F}}={\frac{\mathrm{d}}{\mathrm{d}t}}(m{\vec{v}})}}$ قانون نيوتن الثاني

تاريخ... المفاهيم الأساسية فضاء · زمن · كتلة · قوة طاقة · عزم صيغ ميكانيكا نيوتن ميكانيكا لاگرانج ميكانيكا هاملتونية أقسام ستاتيكا ديناميكا كينماتيكا ميكانيكا تطبيقية ميكانيكا سماوية ميكانيكا متصلة ميكانيكا استاتيكية علماء نيوتن · اويلر · دالمبير · كليرو لاگرانج · لاپلاس · هاملتون · پواسون

البروفسور والتر لوين يشرح قانون نيوتن العام للجاذبية في MIT course 8.01

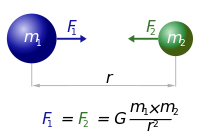
قانون الجذب العام لنيوتن Newton's law of universal gravitation، ينص على أن أي جسمين في الكون توجد بينهما قوة تجاذب تتاسب طرديًا مع حاصل ضرب كتلتيهما، وعكسيًا مع مربع المسافة بينهما. والقانون جزء من الميكانيكا الكلاسيكية وتم صياغته في مؤلف نيوتن الأصول الرياضية للفلسفة الطبيعية، والذي نُشر لأول مرة في 5 يوليو 1687. (عندما عرض الكتاب عام 1686 في الجمعية الملكية، زعم روبرت هوك أن نيوتن حصل على قانون التربيع العكسي منه؛ انظر قسم التاريخ أسفل المقال).

في اللغة المعاصرة، يكتب القانون كالتالي:

Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them:
${\displaystyle{\displaystyle F=G{\frac{m_{1}m_{2}}{r^{2}}}\ }}$, حيث: ${\displaystyle{\displaystyle F\ }}$ هي القوة الناتجة عن الجاذبية ${\displaystyle{\displaystyle G\ }}$ هو ثابت الجذب العام بين الكتل ${\displaystyle{\displaystyle m_{1}\ }}$ هي كتلة الجسيم الأول ${\displaystyle{\displaystyle m_{2}\ }}$ هي كتلة الجسيم الثاني ${\displaystyle{\displaystyle r\ }}$ هو البعد بين الجسيمين

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 أجسام ذات مدى مكاني

Gravitational field strength within the Earth

Gravity field near earth at 1,2 and A

 نموذج المتجه

Field lines drawn for a point mass using 24 field lines

Gravity field surrounding Earth from a macroscopic perspective.

Gravity field lines representation is arbitrary as illustrated here represented in 30x30 grid to 0x0 grid and almost being parallel and pointing straight down to the center of the Earth

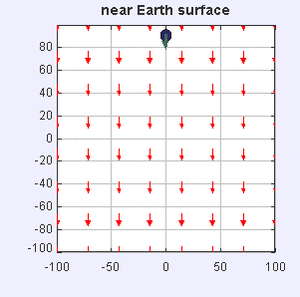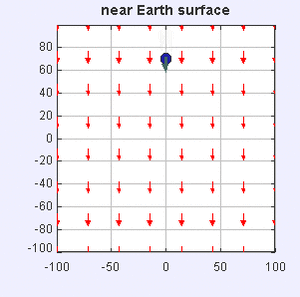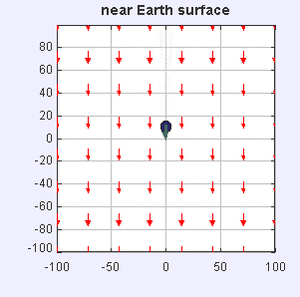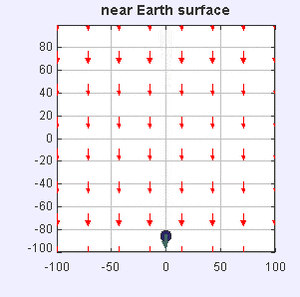
Gravity in a room: the curvature of the Earth is negligible at this scale, and the force lines can be approximated as being parallel and pointing straight down to the center of the Earth

 حقل الجاذبية

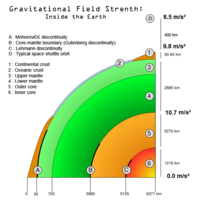
المقالة الرئيسية: حقل الجاذبية

 جوانب إشكالية

${\displaystyle{\displaystyle{\frac{\Phi}{c^{2}}}={\frac{GM_{\mathrm{sun}}}{r_{\mathrm{orbit}}c^{2}}}\sim 10^{-8},\quad\left({\frac{v_{\mathrm{Earth}}}{c}}\right)^{2}=\left({\frac{2\pi r_{\mathrm{orbit}}}{(1\ \mathrm{yr})c}}\right)^{2}\sim 10^{-8}}}$

where r_orbit is the radius of the Earth's orbit around the Sun.

 تحفظات نيوتن

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 ملحقات

${\displaystyle{\displaystyle F=G{\frac{m_{1}m_{2}}{r^{2}}}+B{\frac{m_{1}m_{2}}{r^{3}}}\ }}$ , B a constant

attempting to explain the Moon's apsidal motion. Other extensions were proposed by Laplace (around 1790) and Decombes (1913):

${\displaystyle{\displaystyle F(r)=k{\frac{m_{1}m_{2}}{r^{2}}}exp(-\alpha\cdot r)}}$ (Laplace)

${\displaystyle{\displaystyle F(r)=k{\frac{m_{1}m_{2}}{r^{2}}}(1+{\alpha\over{r^{3}}})}}$ (Decombes)

 حلول لقانون الجذب العام لنيوتن

المقالة الرئيسية: مشكلة الجسم-n

 انظر أيضاً

• متناقضة بنتلي
• قانون الجذب لگوس
• مدار كپلر، تحليل لقوانين نيوتن في تطبيقها على المدارات
• Newton's cannonball
• قوانين الحركة لنيوتن
• Static forces and virtual-particle exchange

 وصلات خارجية

• Feather & Hammer Drop on Moon
• Newton‘s Law of Universal Gravitation Javascript calculator