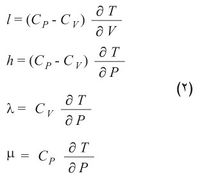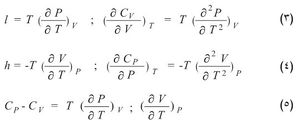ديناميكا حرارية
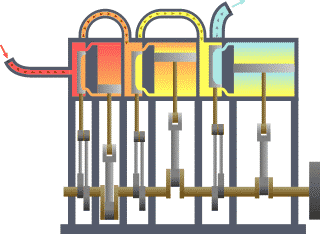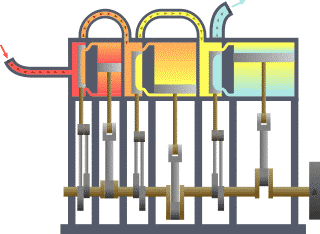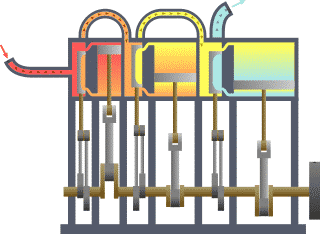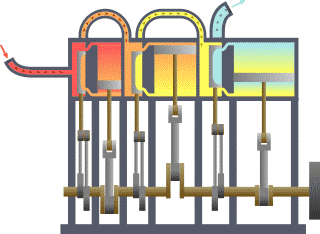 نظام ديناميكي حراري نمطي - الحرارة تنتقل من (المرجل boiler) الساخن إلى (المكثف condenser) البارد, (كلاهما غير ظاهر) وwork يتم استخلاصه, في هذه الحالة بواسطة سلسلة من المكابس. | ||||||||||||
|
مجال الديناميكا الحرارية (إنگليزية: thermodynamics) هو أحد فروع الـفيزياء الذي يدرس ظواهر تحوّلات أنواع وأشكال الـطاقة بما فيها الـحرارة ، ويفحص في أشكال الطاقة لصياغة القوانين التي تحكم انحفاظ الطاقة من شكل إلى شكل ، ويضمن التفاعلات الكيميائية إن كانت واردة ، والإتجاه الذي تفضله الحرارية في انتقالها، والطاقة المتاح تحويلها إلى شغل (work).
وعلى مستو الفيزياء الصـِـغـَرِيـّة (أو الفيزياء المايكرووية) (on the level of microphysics) يقوم هذا العلم باستخدام الميكانيكا الإحصائية لتحقيق أهداف معيـّنة ، من ضمنها نمذجة التصرف الثرموديناميكي من السوائل والغزات (modelling of the thermodynamic behaviour of liquids and gases) ووصف خصائصها مثلاً.
معظم هذه الدراسات تعتمد على فكرة أن أي جملة، أو نظام، معزولة في أي مكان من الكون تحتوي كمية فيزيائية قابلة للقياس ندعوها الطاقة الداخلية للجملة (the inner energy of the system) ويرمز لها بالرمز (U). وتمثل هذه الطاقة الداخلية مجموع الطاقة الكامنة (potential energy) والحركية (kinetic energy) للذرات والجزيئات ضمن الجملة، أي جميع الأنماط التي يمكن أن تنتقل مباشرة كالحرارة، وبالتالي يتم استثناء الطاقة الكيميائية (المختزنة ضمن الروابط الكيميائية)أو الطاقة النووية (الموجودة ضمن نوى الذرات) بإعتبارها أشكال طاقية لا يمكن نقلها ضمن الشروط الطبيعية. تبقى الطاقة الداخلية (U) ثابتة حتى يتم فك العزل عن الجملة فتصبح قادرة على تبادل الطاقة أو المادة من الجملة و إليها، عندئذ يمكن للطاقة الداخلية أن تتغير عن طريق انتقال المادة أو انتقال الحرارة أو انجاز عمل.
التاريخ

 مقالة مفصلة: تاريخ الديناميكا الحرارية
مقالة مفصلة: تاريخ الديناميكا الحرارية
مقدمة
 مقالة مفصلة: قوانين الديناميكا الحرارية
مقالة مفصلة: قوانين الديناميكا الحرارية
يهتم علم الديناميكا الحرارية كما يدل اللإسم بالحرارة أو الطاقة الحرارية بدرجة أولى وبكل الظواهر التي تتمظهر أو تتعلق بهذه الطاقة كعملية إنتقال الحرارة من جسم لآخر أو كيفية تخزين هذه الطاقة أو توليدها. يقوم علم الديناميكا الحرارية على ثلاث قوانين كبرى وهي القانون صفر والقانون الأول والقانون الثاني.
| المتغيرات المترافقة في الديناميكا الحرارية | |
|---|---|
| الضغط | الحجم |
| (الضغط) | (الإجهاد) |
| درجة الحرارة | الإنتروبيا |
| كيمياء محتملة | عدد الجسيمات |
القانون صفر
يتيح هذا المبدأ استخدام موازين الحرارة (مقاييس درجة الحرارة) للمقارنة بين حالات الجمل المختلفة وينص على ما يلي: إذا كان جسم أول A متوازناً حرارياً مع جسم ثانٍ B، وكان الجسم الثاني B في توازن حراري مع جسم ثالث C فإن الجسم A يكون أيضاً في توازن حراري مع C.
القانون الأول
المبدأ الأول أو مبدأ التعادل (التكافؤ) (principle of equivalence): ظهر هذا المبدأ على أنقاض نظرية حفظ السائل الحراري caloric fluid التي وضعت لتشرح ما يحدث عند تماس جسمين مختلفين في درجة الحرارة، فهي تفيد بأن سائلاً حرارياً ما يسري من الجسم الأسخن إلى الجسم الأبرد حتى يحدث تساوي درجتي حرارتيهما. وقد لاحظ ب طمْسون B.Thompson (الملقب بالكونت رمْفورْد) عام 1798م ارتفاع درجة حرارة أسطوانة المدفع عند خرطها في حين لا يكون هناك جسم حار يزوِّدها بالسائل الحراري وفق النظرية السابقة. ووضح بذلك إخفاقها، وتأكد هذا عندما قام همفري ديڤي Humphry Davy بدلْك لوحين من الجليد أحدهما بالآخر فبدأا بالذوبان على الرغم من كون درجتي حرارتهما واحدة، وقد اقترح طمسون بعد هذا أن الحرارة ليست إلا نمطاً من أنماط الطاقة. لكن هذه الفكرة لم تحظ بالاهتمام الكافي وبقيت منسية حتى قرابة عام 1850م، أي حتى قيام العالم الإنكليزي جيمس پرسكوت جول Joule بقياسات كمِّية برهن فيها على التعادل بين كمية الحرارة الناتجة من عملٍ والعملِ نفسه، واستخلص قيمة المعادل الميكانيكي للحريرة. (والحريرة (calorie) هي واحدة كمية الحرارة وهي مما خلّفته نظرية السائل الحراري)، ولكن غالباً ما تقدَّر كمية الحرارة الآن بالجول (وهو واحدة العمل). وفي الوقت نفسه قام العالم الألماني ر. ماير R.Mayer بحساب الفرق بين السعتين الحراريتين: السعة الحرارية تحت ضغط ثابت والسعة الحرارية في حجم ثابت، وبيَّن أن هذا الفرق هو نتيجة صرف عمل معادل (للتغلب على الضغط)، فتوصل إلى قيمة تقارب القيمة التي حصل عليها جول. وتعد صيغة التعادل بين الطاقة الميكانيكية (العمل) والطاقة الحرارية إحدى صيغ المبدأ الأول. غير أن هذا المبدأ يتضمن فكرة أخرى هي تعريف تابع الطاقة الداخلية (internal energy) للجملة المدروسة. فإذا ما تبادلت جملة ترموديناميكية مع الوسط الخارجي كمية من الحرارة Q وعملاً W في تحولات ترموديناميكية مختلفة بين الحالتين نفسيهما (أي على طرق مختلفة بين الحالتين) فإن المجموع الجبري لهما يبقى ثابتاً، ويكتب مساوياً للفرق بين قيمتي تابع الطاقة الداخلية E.
وقد اصطُلح على أن تكون إشارة كلٍ من Q وW موجبة إذا ما دخلت إلى الجملة، كأن تمتص الجملة كمية من الحرارة، وسالبة فيما إذا خرجت منها، كأن تعطي الجملة كمية من الحرارة إلى الوسط الخارجي (ويصطلح بعضهم اصطلاحين مختلفين لكلٍ من كمية الحرارة والعمل المتبادلين فيظهر القانون في صيغة ΔE = Q - W ويُنظر إلى هذا القانون على أنه مبدأ حفظ الطاقة إذا قامت الجملة بدورة مغلقة، فيكون المجموع W+Q منعدماً ومن ثم يكون: E2=E1. كذلك يُعبَّر عن هذا المبدأ أحياناً باستحالة صنع محرك دائم ينتج عملاً من لا شيء، وذلك بالنظر لما يحدث في دورة كاملة فلا بد للجملة إذا ما قدمت عملاً (W-) أن تمتص حرارة. ويُعدّ هذا المبدأ أحياناً أخرى ناجماً عن ضم مبدأ حفظ الطاقة الميكانيكية ونظرية حفظ السائل الحراري إذ يخفق حفظ أي منهما على حدة في حين يكون مجموعهما محفوظاً. ويذهب الفيزيائيون إلى الاعتقاد بأن مبدأ حفظ الطاقة من المبادئ الأساسية في الطبيعة، وكلما ظهر ما يناقضه بادروا إلى تعريف طاقة جديدة، فعندما ظهر مثلاً ما يخرق مبدأ الحفظ هذا في التفاعلات النووية افتُرض وجود الطاقة الناتجة عن نقصان الكتلة ومن ثم التعادل بين المادة والطاقة، وبقي قانون حفظ الطاقة سارياً، ويعد الآن الصيغة النهائية للمبدأ الأول.
القانون الثاني
يتعلق القانون الثاني بالانتروبية او الاعتلاج ومفاده أن تدفق الإنتروپية إلى داخل النظام ناقص تدفق الإنتروبية إلى خارج النظام زائد الإنتروبية المتكونة داخل النظام تساوي صفر. تناول هذا المبدأ في أول ظهوره عمل المحركات الحرارية والمبرِّدات، أي تحويل الحرارة إلى عمل وانتقال الحرارة. فوضع حداً أعلى لمردود المحركات الحرارية وبيَّن طرائق تحسين أدائها؛ ولهذا المبدأ صيغ عديدة يمكن البرهان على تكافئها بمحاكمة منطقية. وعلى الرغم من أن اختراع المحرك البخاري يعود إلى العام 1765م من قِبل جيمس واط James Watt فإن ظهور القانون الثاني الذي يبيّن سلوك المحركات الحرارية تأخر حتى منتصف القرن التاسع عشر، عندما أعلن عنه كلٌ من رودلف كلاوزيوس (1850م) Rudolf Clausius وكلڤن Kelvin في صيغتين مختلفتين. وتنص صيغة كلفن على «استحالة استخلاص عمل ميكانيكي بأي وساطة مادية، من أي جزء من المادة، بتبريده إلى درجة حرارة أخفض من أخفضِ درجات حرارة الأجزاء المحيطة به». أما صيغة كلاوزيوس فتنص على «أنه يستحيل انتقال كمية من الحرارة من منبع بارد إلى منبع أسخن منه تلقائياً، أي من غير الاستعانة بمنبع طاقة خارجي». وأما صيغة ماكس پلانك Max Planck فتنص على «استحالة صنع محرك يعمل في دورة كاملة تكون نتيجتها الوحيدة إنجاز عمل ميكانيكي بتبريد منبع حراري وحيد». وهي صيغة تعني استحالة صنع آلة دائمة الحركة من النوع الثاني تعمل على منبع وحيد. وتشترك هذه الصيغ الثلاث في كونها صيغاً نافية، ويسوِّغ صدقها بطريقة نقض الفرض. وقد حاول أحد المهندسين اللامعين هو المهندس سادي كارنو Sadi Carnot معالجة مردود المحركات معالجة نظرية وانتهى إلى صيغة للمبدأ الثاني سميت باسمه عام 1824م أعيد اكتشافها وصوغها فاستخدمت للتوفيق بين الصيغ المختلفة.
وقد لاحظ كارنو الارتباط الوثيق بين التحولات الطبيعية والتحولات اللاعكوسة وكذلك انخفاض مردود المحرك كلما ابتعدت التحولات التي يعمل عليها عن العكُوسة. لذلك تخيل محركاً مثالياً يقوم بدورة مكونة من تحولات عكوسة، وبرهن على أن لهذا المحرك أفضل مردود. ويؤدي هذا إلى صيغة أخرى مستمدة من أعمال كارنو تنص على أن جميع مردودات محركات كارنو التي تعمل بين المنبعين نفسيهما متساوية بغض النظر عن المادة المستخدمة فيها. مما يدعو إلى القول بأن مردود أي منها لا يتعلق إلا بدرجتي حرارة المنبعين فقط.
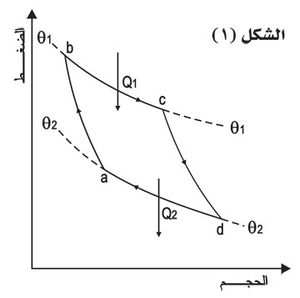
تصور كارنو التحولات في الدورة العكوسة المسماة باسمه، فذكر أن أقرب التحولات إلى العكُوسة، مع امتصاص كمية من الحرارة أو إعطائها، هو التحول المتساوي الدرجة (isothermal) ويحتاج الأمر إلى تحوّلين على الأقل في هذه الدورة بمتغيـّرين من درجة الحرارة و ، ووصَل بينهما بتحوّلين لا يتم فيهما تبادل حراري مع الوسط الخارجي أي تحوّلين كظومين (two adiabatic changes)، ويبين الشكل (١) دورة كارنو المؤلفة من تحولين متساويي الدرجة cd وab وتحولين كظومين bc وda. فإذا كانت Q1 كمية الحرارة المتبادلة مع المنبع الأول T1 وQ2 كمية الحرارة المتبادلة مع المنبع الثاني T2، وكان المردود مستقلاً عن المادة العاملة وتابعاً لدرجتي حرارة المنبعين فقط، يمكن تبيان وجوب كون:
حيث أن و يمثـّلان متغيـّرين من درجة الحرارة.
وقد اختار كلفن أبسط تبعية لـ g وهي التبعية الخطية ووضع أخيراً المعادلة على النحو التالي:
ويمكن بهذا إنشاء سلم حراري استناداً إلى تخيل محركات تعمل بين منبع حراري عياري وأجسام يراد قياس درجة حرارتها؛ فبقياس كميات الحرارة المتبادلة ونسبة بعضها إلى بعض، وكذلك باختيار درجة حرارة عيارية للمنبع يمكن إعطاء درجات حرارة لهذه الأجسام. ويسمى سلم درجات الحرارة هذا، بسبب اعتماده على قوانين الترموديناميك، سلم الحرارة الترموديناميكي، ويسمى أيضاً سلم كلفن لاختيار كلفن التبعية الخطية البسيطة، لذا يرمز لدرجات الحرارة فيه بالحرف الأول من اسم كلفن K. لقد تم اختيار الماء عندما يكون متوازناً في أطواره الثلاثة (النقطة الثلاثية) ليكون المنبع العياري وقد أسند إلى درجة حرارته عندئذ الرقم 273.13K ليتطابق قياس درجة الحرارة فيه مع قياس الدرجة في السلم المئوي أو سلم سلزيوس (Celsius).
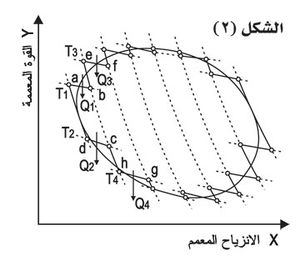
وقد تم فيما بعد تعميم محاكمة كارنو على أي دورة مغلقة عكوسة، فأمكن البرهان على إمكان تقسيمها إلى عدد من دورات كارنو المكافئة (الشكل (٢))، فأمكن الحصول على تعبير يتضمن تعريف تابع جديد، كما في حالة الطاقة الداخلية، هو تابع حالةٍ مستقلٍ عن الطريق المسلوك، سمي هذا التابع تابع الأنتروبية S، وقد يُعرف بصورة تفاضلية على النحو: في تحول عكوس.
فإذا فرض الآن أن الجملة المدروسة تقوم بتحول متساوي الدرجة كان تغير أنتروبية الجملة مساوياً ، أما تغير أنتروبية الوسط الخارجي، وهو المنبع في هذه الحالة، فيساوي ويكون بالتالي تغير الأنتروبية الكلي في هذا التحول العكوس المتساوي الدرجة معدوماً. ولو حسب تغير الأنتروبية الكلي في تحول غير عكوس مثل انتقال الحرارة عبر جملة من المنبع الحار T1 إلى المنبع البارد T2 فقط وتعود فيه الجملة في نهاية الدورة إلى ما كانت عليه فإن تغير الأنتروبية في هذه الدورة هو تغير أنتروبية المنبعين فقط. أما تغير أنتروبية المنبع الحار فهو - وأما تغير أنتروبية المنبع البارد فهو ، وبما أن T2 > T1 فإن تغير الأنتروبية الكلي يكون موجباً، أي إن الأنتروبية تزداد في هذا التحول غير العكوس. وفي الواقع يمكن البرهان على أن هذه النتيجة عامة في كل التحولات غير العكوسة وتعد صيغة من صيغ المبدأ الثاني. وينطبق ذلك على التحولات الطبيعية لأنها تحولات غير عكوسة ويسمى المبدأ عندئذ مبدأ تزايد الإنتروبية.
القانون الثالث

يتناول المبدآن الأول والثاني علاقات بين تغيرات توابع الجملة والكميات المتبادلة مع الوسط الخارجي، فهي إذن معادلات فروق بين قيمتيْ تابع، في حين يتناول المبدأ الثالث تحديد القيمة المطلقة (absolute value) للأنتروبية، وذلك بتحديد قيمتها عند درجة حرارة الصفر المطلق. وقد ظهرت الحاجة إلى هذا المبدأ عندما أمكن الحصول على درجات حرارة أقل كثيراً من الصفر المئوي، حين أمكن تمييع الغازات ولاسيما النادرة منها. وقد كان قياس السعة الحرارية للأجسام الصلبة من أهم ما دُرس في مثل هذه الدرجات المنخفضة؛ وقد تبيَّن عدم ثبات قيمتها وانخفاضها بنقصان درجة الحرارة خلافاً لما تتوقعه النظرية التقليدية من ثباتها. وقد لاحظ العالم الألماني ڤالتر نِرنست Walter Nernst عام 1906 أن السعات الحرارية للأجسام الصلبة تسعى كلها إلى الصفر مع اقتراب درجة حرارتها من الصفر المطلق، فعُدَّ ذلك صيغة أولى للمبدأ الثالث؛ وقد قام نِرْنست بدراسة جمل غازية وجمل ترموديناميكية مختلفة فتبين له أن تغير الأنتروبية المرافق لتحولٍ متساوي الدرجة يقترب من الصفر مع اقتراب درجة حرارة الجملة المكثفة (الجامدة أو السائلة) من الصفر المطلق، وهذه هي صيغة نرنست للمبدأ الثالث. أما صيغة نرنست ـ بلانك فهي: إن أنتروبية جميع الأجسام تتناهى إلى قيمة حدية واحدة قد تساوي الصفر مع انتهاء درجة حرارتها نحو الصفر المطلق، وتجعل هذه الصيغة اتخاذ درجة حرارة الصفر المطلق مبدأً لحساب الأنتروبية فتقوم في هذه الدرجة مقام ثابتة اختيارية للإنتروبية.
ويصاغ هذا المبدأ الثالث صيغة مختلفة مستمدة من التقنيات التجريبية الهادفة إلى تخفيض درجة الحرارة، فقد لوحظ تزايد الصعوبة في الحصول على درجات الحرارة المنخفضة كلما اقتُرب من الصفر المطلق، فصيغ المبدأ الثالث صيغة لا وصولية (unattainable) تنص على استحالة الوصول بجملةٍ ما إلى درجة حرارة الصفر المطلق باتباع عدد محدودٍ من التحولات مهما كانت الجملة وكيفما كانت الطريقة.
تطبيقات القوانين الثلاث
1ـ سلم درجات الحرارة المطلق وسلم كلفن الثرموديناميكي: لقد قادت صيغة كارنو للمبدأ الثاني إلى طريقة موحدة لتحديد درجات حرارة الأجسام المختلفة وأدت إلى سلم كلفن. وأمكن عملياً تطبيق هذه الطريقة بجعل المادة العاملة غازاً ذا ضغط منخفض ليقترب مما يسمى بالغاز المثالي الذي يخضع للمعادلة التالية، من أجل جزيء غرامي، حيث ثابتة الغازات العامة وθ درجة حرارة الغاز التي تحسب من حاصل ضرب الضغط p في الحجم V. ويتبيـّن تطابقها مع T إذا ما حسبت Q1 وQ2 للغاز فيكون:
حيث:
- p: ضغط الغاز
- V: حجم الغاز
- n: عدد المولات في الغاز
- : ثابت الغازات العام
- T: درجة الحرارة المطلقة.
وهي مطابقة للمعادلة المقترحة لإنشاء سلم كلفن. لهذا كانت موازين الحرارة الغازية هي المرجع الموثوق الوحيد حتى عهد قريب ويسمى سلّمها أحياناً السلم المطلق لأن صفره محدّد لجميع الأجسام.
2ـ الفرق بين السعتين الحراريتين Cp وCv: يمكن اعتماداً على كون تابع الأنتروبية S تابع حالة، وبالتالي فإن تغير قيمته بين حالتين مستقل عن الطريق المسلوك. حساب السعة الحرارية Cp تحت ضغط ثابت والسعة الحرارية Cv في حجم ثابت، لنحصل على صيغة للفرق بينهما.
3ـ التوابع الثرموديناميكية الأخرى: يمكن استخلاص توابع ثرموديناميكية جديدة باستعمال تابع الأنتروبية فيكتب القانون الأول مبدأً في حالة التحولات العكوسة لجملة متجانسة بدلالة الأنتروبية استناداً إلى القانون الثاني على النحو التالي:
ففي حالة تحول كظوم (لا تتبادل فيه الجملة مع الوسط الخارجي حرارة)، ولا يتغير فيه الحجم أيضاً تكون الطاقة الداخلية E ثابتة فيوصف التحول بأنه تحول ثابت الطاقة وكثيراً ما يُسهِّل وصف التحولات استخدام مثل هذه التوابع. فمثلاً، تجري الكثير من التحولات تحت ضغط ثابت (الضغط الجوي غالباً) ولا يظهر تغير الضغط في علاقة dE السابقة صراحة، لذلك يُعرف تابع جديد مثل الإنطلبية H بأنه:
H = E + PV
وتكون الإنطلبية ثابتة أي يكون هذا التابع ثابتاً إذا كان التحول كظوماً (TdS = 0) ويجري في ضغط ثابت (dp = 0). وإذا أريد دراسة تحولات متساوية الدرجة مثلاً وتجري تحت ضغط ثابت يُستعمل تابع جيبس G للطاقة الحرة المعرّف بالعلاقة
G = E + PV - TS
فتكون طاقة جيبس عندئذ ثابتة (dT= 0 وdp = 0). كما يُستخدم نظرياً تابع هلمهولتز F للطاقة الحرة الذي يعرف على النحو
F = E - TS
وتفيد هذه التوابع كثيراً في التحولات الكيميائية بعد تعميمها.
4ـ الترموديناميك الكيميائي: يمكن تعميم القانون الثاني الذي يحدد اتجاه التحولات الطبيعية من معرفة ما إذا كانت الأنتروبية ستزداد في هذا التحول أم لا، أو من تناقص تابع جيبس في هذا التحول. ويأتي التعميم من النظر في جملة غير متجانسة، أي جملة تحوي عدة أطوار سائلة وصلبة وغازية مثلاً، أو النظر في جملة مركبة من عدة أنواع من الذرات كخليط من الغازات أو مزيجٍ سائل من عدة مواد، فتدخل عندئذ نسبة كمية طور معين إلى كمية الجملة الكلية أو نسبة عدد الذرات من نوع معين إلى عدد الذرات الكلي، أي التراكيز بصورة عامة، فتظهر متحولات جديدة تتغير بتغير الشروط الخارجية. وتدخل هذه المتحولات على غرار متحولات الحجم أو الأنتروبية أو درجة الحرارة أو الضغط كما تؤدي إلى ظهور ما يعرف بالكمون الكيميائي m1 المتعلق بتغير تركيز الطورi. يهتم الفيزيائيون في حالة جملة ذات أطوار عدة بكمية كل طور والشروط الخارجية لوجودها معاً في حالة توازن، في حين يهتم الكيميائيون بالتفاعلات التي تجري بين مواد مختلفة يمكن فيها النظر إلى جملة المواد الداخلة والمواد الناتجة بوصفها جملة ترموديناميكية واحدة. ويزودنا الكمون الكيميائي لكل نوع من التفاعلات بمعلومات عن اتجاه التفاعل وحتى سرعته أحياناً؛ وذلك بحساب قيم تغيرات التوابع الترموديناميكية مثل طاقة جيبس G والإنطلبية H المقابلة لهذا التفاعل. ولأهمية معرفة هذه القيم للكيميائيين ظهر فرع خاص سمي الترموديناميك الكيميائي.
الثرموديناميكا الإحصائية
يتطلب دخول البنية الذرية للمادة وأن أية جملة مكونة من عدد كبير من الذرات إلى اتصال مع الميكانيك الإحصائي التقليدي ولذلك ظهر ما يعرف بالترموديناميكا الإحصائية، إن إخفاق قوانين نيوتن في وصف سلوك الذرات وصفاً كاملاً، وظهور ميكانيك الكم بديلاً عن ميكانيك نيوتن أدى إلى تطور آخر في الثرموديناميكا يعمم الأفكار السابقة الواردة في الميكانيكا الإحصائية التقليدية. فوضعت مسلَّمات هي أركان في بناء جديد سمي الثرموديناميكا الإحصائية أو الميكانيكا الإحصائية الكمومي، ويفضل بعضهم تسميته الفيزياء الإحصائية.
ثرموديناميكا التحولات اللاعكوسة
تتناول العلاقات الثرموديناميكية السابقة قيم المقادير بين حالتين توازنيتين للجملة، أي علاقات لا يكون الزمن فيها متحولاً، كما لا تبحث هذه العلاقات في معدّلات حدوث التحولات. إن إدخال الزمن ومعدَّلات الحدوث أمر ضروري في الواقع لدراسة الظواهر الحقيقية الفيزيائية والكيميائية والحيوية دراسة كمية، وهي ظواهر تتصف بأنها لا عكوسة (irreversible). وقد بدأ بعض العلماء النظر فيها حديثاً ومنهم لارس أونْزاگر Lars Onsager عام 1931م ومازالت دراستها قيد التطور حتى اليوم. إن دراسة الظواهر اللاعكوسة تختلف عنها في الظواهر العكوسة في وجوب أن يؤخذ تطور الجملة الداخلي في الحسبان، إضافة إلى التبادل مع الوسط الخارجي؛ فيكتب تغير الأنتروبية الكلي على الصورة
- dS = deS + diS ،
حيث deS هي الأنتروبية المتبادلة مع الوسط الخارجي (وهي الأنتروبية الوحيدة إذا كان التحول عكوساً)، وحيث diS قيمة موجبة دوماً وتوافق تولد أنتروبية داخلية في الجملة. ومن المناسب، بالمقابل، بيان أنه، لدى حساب تولدٍ موضعي للأنتروبية مهما كان ذلك، تُستخدم في دراسة الظواهر اللاعكوسة علاقاتُ الثرموديناميكا التقليدية بافتراض توازن موضعي في كل نقطة من جملة تتطور تطوراً كلياً.
والميزة الأخرى للتحولات اللاعكوسة هي إدخال عامل الزمن t في وصف الظواهر، فمن المهم أن يؤخذ بالحسبان معدّل تولد الأنتروبية . وتتناسب P هنا مع تدرج T كما تتناسب مع ، وهو تدفق الحرارة الذي يتناسب هو أيضاً مع تدرج T. وقد أسهم ثرموديناميكا الظواهر اللاعكوسة (thermodynamics of irreversible phenomena) في إيجاد حلول مرضية ولاسيما في حالات الظواهر المتزاوجة إذ تفترض النظرية التقليدية، خلافاً لما هو جلي بداهة، عكوسية الظواهر مثل ظواهر الآثار الكهرحرارية التي يشوبها باللاعكوسية أثر جول وكذلك الناقلية الحرارية.
كمائن ثرموديناميكية
 مقالة مفصلة: كمون ترموديناميكي
مقالة مفصلة: كمون ترموديناميكي
وكما يمكن استنباطه من معادلة توازن الطاقة في نظام ديناميكي حراري ، فإنه يوجد كميات طاقة تسمى «الكمائن الثرموديناميكية» (thermodynamic potentials) , وهي المقياس الكمي للطاقة المختزنة في النظام. وأهم خمس جهود معروفين هم:
| طاقة داخلية | |
| طاقة هلمهولتس الحرة | |
| إنثالپيا | |
| طاقة گيبس الحرة | |
| كمون كبير grand potential |
قوانين أخرى
من أهم الخصائص المدروسة
- الحرارة T
- الضغط p
- الحجم V
- الطاقة الداخلية U
- الـإنتروبية أو الإعتلاج S
- الـإنتالبية H (التغير في الانثالبي تساوى التغير في الطاقه عند ثبوت الضغط لان H=pV+U)
- الـسرعة
- الارتفاع
ويمكن تقسيم هذه الخصائص إلى :
- حالية حرارية (كالحرارة والضغط والحجم) أو حالية كالورية (كالطاقة الداخلية والإعتلاج والإنتلبية)
- حالية (أي انها تعبر عن حالة للمادة وهي كل الخصائص المذكورة أعلاه) وعملياتية ( أي أنها لا تو جد إلا بو جود عملية كعملية إنتقال الحرارة من جسم للآخر، وعلى ذلك فهي تمثل تغير حالة المادة. من هذه الخصائص الشغل)
المعادلة الحرارية
من أهم القوانين التي ترسم العلاقة بين الضغط و الحرارة والحجم و الكتلة في الغازات:
PV=mRiT
حيث Ri هو الثابت الغازي ولكن هذه العلاقة ليست الوحيدة وهي كذلك ليست صحيحة صحة مطلقة حيث أنه أعتمد في إشتقاقها على بعض المسلمات التي تمثل تبسيطا للواقع. حيث تم الحساب بالغازات المثالية أي أن ذرات أو جزيئات الغاز ليس لها حجم و أنه لا توجد قوى بين الموليكولات كما أن الجزيئات لا تغير شكلها أي بمعنى في حالة تصادم جزيئين فإن التصادم يكون مطاطاً وكل هذه مسلمات غير واقعية ولكن المعادلة التي نحصل عليها تسمح لنا بإستعمالها في مجالات معينة لا نحتاج فيها لدقة كبيرة.
معادلة فان دا فالس
معادلة فان دا فالس هي أيضا معادلة حرارية ( معادلة تحتوي على خصائص حرارية تسمى معادلة حرارية).
(p+(a/v²)*(v-b)=Ri*T
حيث a و b تصحيح للمسلمات الخاطئة أعلاه.
أنواع تغير الحالة
المعاملات الديناميكية الحرارية thermodynamic coefficients
تتبع خصائص الجسم المتجانس ذي الكتلة المعروفة في وضع التوازن الترموديناميكي لمتحولين مستقلين هما، على سبيل المثال، الضغط ودرجة الحرارة أو الضغط والحجم أو قرينة الانكسار ودرجة الحرارة. وإذا أخذت بالحسبان المتحولات الثلاثة: الضغط P والحجم V ودرجة الحرارة T لوجد أن هذه المقادير مرتبطة بعضها ببعضها الآخر بعلاقة تعرف بمعادلة الحالة f (P, V, T,) =0. وارتباط هذه المتحولات الثلاثة بعضها ببعضها الآخر يعطي سلسلةً من العلاقات بين مجموعة من المعاملات التي يكتسب تعيينها في حالة التحولات الصغيرة والعكوسة أهمية تطبيقية كبيرة. وهذه العلاقات لاتضيف جديداً إلى المبدأ الأول أو المبدأ الثاني في الترموديناميك (التحريك الحراري). فإذا عبِّر رياضياً عن كمية الحرارة dQ المقدمة إلى (أو المسحوبة من) جملة ما عند تحول صغيرٍ فيه (حيث تتغير درجة الحرارة بمقدار dT والضغط بمقدار dP والحجم بمقدار dV) من خلال هذه المتحولات الترموديناميكية الثلاثة مثنى مثنى لوُجد ما يأتي:
أي إن كمية الحرارة ترتبط بهذه الأزواج الثلاثة من المتحولات بثلاثة أزواج من المعاملات هي Cv و l أو Cp و h أو λ و μ. وهذا يعني أنه يلزم استخدام ستة معاملات: اثنان منها فقط مستقلان لأن كل واحدة من المعادلات السابقة مكافئة للمعادلتين الأخريين. ويمكن ربط المعاملات المذكورة أعلاه بخصائص ترموديناميكية محددة للجملة هي السعة الحرارية عند ثبات الحجم Cv والسعة الحرارية عند ثبات الضغط Cp ومعامل التمدد الحجمي α والانضغاطية الحرارية β كما يأتي:
l = Tα/ β; h = Tα/ β; λ = Cvβ /α ; m = Cp/V α.
إن بالإمكان التعبير أيضاً عن بقية المعاملات الأربعة بدلالة المعاملين Cp و Cv وبدلالة المتحولات الترموديناميكية.
ويمكن الاستفادة من حقيقة كون تغير الطاقة الداخلية dU وكذلك تغير الأنتروبية dS= dQ/T تفاضلاً كاملاً في الحصول على علاقات تطبيقية مفيدة:
انظر أيضاً
- ديناميكا حرارية جزيئية (molecular thermodynamics)
- سعة حرارية الخاص Cp، Cv
- قانون بويل
مراجع
- ^ Schools of thermodynamics - EoHT.info.
مصادر
- Turns, Stephen (2006). Thermodynamics: Concepts and Applications. Cambridge University Press, Cambridge.ISBN 0-521-85042-8
- Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics. 2nd ed. John Wiley & Sons, Inc., New York. ISBN 0-471-86256-8
قراءات إضافية
- Ben-Naim, Arieh (2007). Entropy Demystified. World Scientific. ISBN 981-270-055-2.
- Dugdale, J. S. (1996). Entropy and its Physical Meaning (2nd Ed. ed.). Taylor and Francis (UK); CRC (US). ISBN 0748405690.
{{cite book}}:|edition=has extra text (help) - Fermi, Enrico (1937). Thermodynamics. Prentice Hall. ISBN 0-486-60361-X.
- Kroemer, Herbert, and Kittel, Charles (1980). Thermal Physics (2nd Ed. ed.). W. H. Freeman Company. ISBN 0-7167-1088-9.
{{cite book}}:|edition=has extra text (help)CS1 maint: multiple names: authors list (link) - Penrose, Roger (2005). The Road to Reality : A Complete Guide to the Laws of the Universe. ISBN 0-679-45443-8.
- Reif, F. (1965). Fundamentals of statistical and thermal physics. McGraw-Hill. ISBN 0-07-051800-9.
- Goldstein, Martin; Inge, F (1993). The Refrigerator and the Universe. Harvard University Press. ISBN 0-674-75325-9.
{{cite book}}: CS1 maint: multiple names: authors list (link) - vonBaeyer; Hans Christian (1998). Maxwell's Demon: Why Warmth Disperses and Time Passes. Random House. ISBN 0-679-43342-2.
{{cite book}}: CS1 maint: multiple names: authors list (link)
وصلات خارجية
- فوزي عوض. "التحريك الحراري (الترموديناميك)". الموسوعة العربية.
- Entropy - A Basic Understanding A primer for entropy from a chemical perspective
- Max Jammer (1973). Dictionary of the History of Ideas: Entropy
- Frank L. Lambert; entropysite.com – links to articles including simple introductions to entropy for chemistry students and for general readers.
- Thermodynamics - a chapter from an online textbook
- Entropy on Project PHYSNET
- Entropy Journal - a free journal on Entropy