قانون الغازات المثالية
| الديناميكا الحرارية |
|---|
 |
قانون الغازات المثالية ideal gas law، يسمى أيضاً قانون الغازات العامة general gas equation، هو معادلة حالة لغاز مثالي افتراضي. وهو تقدير جيد لسلوك العديد من الغازات تحت ظروف متعددة، على الرغم من أوجه قصوره المختلفة. أعلن عنه لأول مرة إميل كلاپيرون عام 1834 كمزيج بين قوانين بويل، تشارلز، أڤوگادرو، وگي-لوساك التجريبية.[1]
المتغيرات التي منها تعرف كمية الغاز وحالته هي الضغط، الحجم والحرارة طبقا للقانون التالي: ح ض = ر ن د
حيث:
- ض أو p: ضغط الغاز
- ح أو V: حجم الغاز
- ن أو n: عدد المولات في الغاز
- ر أو R: ثابت الغازات العام
- د أو T: درجة الحرارة المطلقة.
حيث أن قانون الغازات المثالية يتجاهل كلا من الحجم الجزيئي والتفاعلات بين الجزيئات وبعضها، يعد قانون الغازات المثالية أكثر دقة مع الغازات أحادي الذرة في الضغوط المنخفضة ودرجات الحرارة العالية. يكون تجاهل الحجم الجزيئي أقل أهمية كلما ازداد الحجم، أي عند الضغوط المنخفضة. الأهمية النسبية للتفاعلات الجزيئية تضعف بزيادة الطاقة الحرارية أي بزيادة الحرارة.
- الغازات أحادية الذرة مثل الهليوم والكريبتون وغيرها هي كلها من الغازات الخاملة حيث لا ترتبط الذرات مع بعضها البعض مكونة جزيئات وإنما تبقى كل ذرة بمفردها. هذا بالمقارنة بغاز ثنائي مثل الأكسجين والنيتروجين والكلور كلجزيئ منها مكون من ذرتين. ومثال على جزيئ ثلاثي الذرات : ثاني أكسيد الكربون وجزيئه يتكون من 1 ذرة كربون و 2 ذرة أكسجين. وتعتبر الجزيئات الأحادية الذرات أبسط أنواع الغازات في الدراسة وتسمي لذلك غاز مثالي. الغازات الثنائية والثلاثية الذرات والجزيئات الأعقد من ذلك يحدث فيها اهتزاز الذرات وكذلك يمكنها "الدوران" حول محور أو أكثر ، مما يصعب دراستها.
وضعت معادلات أكثر تعقيدا مثلا معادلة فان دير فالس والتي تسمح بادخال الحجم الجزيئي والتفاعلات بين الجزيئات في الاعتبار.
المعادلة
تصف المعادلة العامة حالة غاز مثالي من حيث دوال الحالة : الضغط p والحجمV ودرجة الحرارةT وكمية الغاز n وعدد جزيات الغاز N ، وبالتالي كتلة الغاز m. ويمكن كتابة المعادلة في صياغات مختلفة، ولكنها جميعا متساوية ، وكل منها يصف حالة النظام بدقة كاملة.
الصيغ الشائعة
الصياغات الأكثر شيوعاً في الاستخدام هي:
- هو الضغط المطلق للغاز،
- هو حجم الغاز،
- هو amount of substance of gas (also known as number of moles),
- هو ثابت الغاز المثالي، أو العام،، ويساوي حاصل ضرب ثابت بولتسمان و ثابت أڤوگادرو،
- هو ثابت بولتسمان،
- هو ثابت أڤوگادرو،
- هو درجة الحرارة المطلقة للغاز،
- هو عدد جسيمات (عادةً الذرات والجزيئات) من الغاز.
In SI units, p is measured in pascals, V is measured in cubic metres, n is measured in moles, and T in kelvins (the Kelvin scale is a shifted Celsius scale, where 0.00 K = −273.15 °C, the lowest possible temperature). R has for value 8.314 J/(mol·K) = 1.989 ≈ 2 cal/(mol·K), or 0.0821 L⋅atm/(mol⋅K).
الصيغة المولية
How much gas is present could be specified by giving the mass instead of the chemical amount of gas. Therefore, an alternative form of the ideal gas law may be useful. The chemical amount, n (in moles), is equal to total mass of the gas (m) (in kilograms) divided by the molar mass, M (in kilograms per mole):
By replacing n with m/M and subsequently introducing density ρ = m/V, we get:
Defining the specific gas constant Rspecific as the ratio R/M,
This form of the ideal gas law is very useful because it links pressure, density, and temperature in a unique formula independent of the quantity of the considered gas. Alternatively, the law may be written in terms of the specific volume v, the reciprocal of density, as
It is common, especially in engineering and meteorological applications, to represent the specific gas constant by the symbol R. In such cases, the universal gas constant is usually given a different symbol such as or to distinguish it. In any case, the context and/or units of the gas constant should make it clear as to whether the universal or specific gas constant is being used.[2]
الميكانيكا الإحصائية
In statistical mechanics, the following molecular equation is derived from first principles
where P is the absolute pressure of the gas, n is the number density of the molecules (given by the ratio n = N/V, in contrast to the previous formulation in which n is the number of moles), T is the absolute temperature, and kB is the Boltzmann constant relating temperature and energy, given by:
where NA is the Avogadro constant.
From this we notice that for a gas of mass m, with an average particle mass of μ times the atomic mass constant, mu, (i.e., the mass is μ Da) the number of molecules will be given by
and since ρ = m/V = nμmu, we find that the ideal gas law can be rewritten as
In SI units, P is measured in pascals, V in cubic metres, T in kelvins, and kB = 1.38×10−23 J/K in SI units.
قانون الغازات المجمع
Combining the laws of Charles, Boyle and Gay-Lussac gives the combined gas law, which takes the same functional form as the ideal gas law says that the number of moles is unspecified, and the ratio of to is simply taken as a constant:[3]
where is the pressure of the gas, is the volume of the gas, is the absolute temperature of the gas, and is a constant. When comparing the same substance under two different sets of conditions, the law can be written as
في تلك المعادلات تعني الرموز الآتية ما يلي:
- kB - ثابت بولتزمان
- Rm - ثابت الغازات العام (أو ثابت الغازات المولي)
- Rs - ثابت الغاز النوعي
- ρ - الكثافة
- vm - الحجم المولي
- v - الحجم النوعي
- N - عدد الجزيئات
- n - عدد المولات
- m - الكتلة
- M - كتلة مولية
تمثل المعادلة العامة للغاز المثالي معادلة الحالة الترموديناميكية عندما تكون الكثافة صغيرة dar, أي عندما يكون الضغط صغيرا جدا ودرجة الحرارة عالية. في تلك الحالة يمكن إهمال حجم الجزيئات نفسها وقوى التجاذب بينها.
وتمثل معادلة الغاز المثالي تمثيلا تقريبيا لغازات كثيرة مثل الهواء المشبع ببخار الماء في الظروف الطبيعية (1 ضغط الجوي ،و درجة حرارة 20 مئوية) ، فهي تصف حالته بدقة تقريبية مناسبة. وينتج من المعادلة العامة للغاز المثالي أن الطاقة الداخلية للغاز المثالي لا تعتمد على الضغط أو الحجم ، وتعتمد فقط على درجة الحرارة. وتتكون الطاقة الداخلية في هذه الحالة من طاقة الحركة والحركة الحرارية لجزيئات الغاز.
في عام 1873 أضاف الفيزيائي فان ديرفال المعادلة المعروفة باسمه معادلة فان دير فال الحجم الذاتي لجزيئات الغاز وقوي التجاذب على المعادلة العامة وأصبحت معادلته بذلك تنطبق أيضا على الغازات الحقيقية.
ولا ينطبق تأثير جول-تومسون على الغاز المثالي.
الطاقة المرتبطة بالغاز
| طاقةالغاز | الصيغة الرياضية |
|---|---|
| الطاقة المرتبطة بمول واحد من الغاز | |
| الطاقة المرتبطة بگرام واحد من الغاز | |
| الطاقة المرتبطة بجزيء واحد من الغاز |
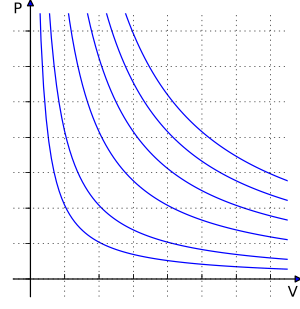
التطبيقات على العمليات الديناميكية الحرارية
| العملية | الثابت | النسبة المعروفة أو دلتا | P2 | V2 | T2 |
|---|---|---|---|---|---|
| عملية تساوي درجة الحرارة | P2 = P1 | V2 = V1(V2/V1) | T2 = T1(V2/V1) | ||
| P2 = P1 | V2 = V1(T2/T1) | T2 = T1(T2/T1) | |||
| Isochoric process (Isovolumetric process) (Isometric process) |
P2 = P1(P2/P1) | V2 = V1 | T2 = T1(P2/P1) | ||
| P2 = P1(T2/T1) | V2 = V1 | T2 = T1(T2/T1) | |||
| Isothermal process | P2 = P1(P2/P1) | V2 = V1/(P2/P1) | T2 = T1 | ||
| P2 = P1/(V2/V1) | V2 = V1(V2/V1) | T2 = T1 | |||
| Isentropic process (عملية كظومة عكسية) |
P2 = P1(P2/P1) | V2 = V1(P2/P1)(−1/γ) | T2 = T1(P2/P1)(γ − 1)/γ | ||
| P2 = P1(V2/V1)−γ | V2 = V1(V2/V1) | T2 = T1(V2/V1)(1 − γ) | |||
| P2 = P1(T2/T1)γ/(γ − 1) | V2 = V1(T2/T1)1/(1 − γ) | T2 = T1(T2/T1) | |||
| Polytropic process |
P2 = P1(P2/P1) | V2 = V1(P2/P1)(-1/n) | T2 = T1(P2/P1)(n − 1)/n | ||
| P2 = P1(V2/V1)−n | V2 = V1(V2/V1) | T2 = T1(V2/V1)(1 − n) | |||
| P2 = P1(T2/T1)n/(n − 1) | V2 = V1(T2/T1)1/(1 − n) | T2 = T1(T2/T1) | |||
| Isenthalpic process (عملية كظومة غير عكسية) |
P2 = P1 + (P2 − P1) | T2 = T1 + μJT(P2 − P1) | |||
| P2 = P1 + (T2 − T1)/μJT | T2 = T1 + (T2 − T1) |
الانحرافات عن السلوك المثالي للغازات الحقيقية
الاشتقاقات
التجريبية
النظرية
النظرية الحركية
تنص نظرية ديناميكا الغازات على أن الغازات تتكون من ذرات منفردة أو جزيئات منفردة ، وكل منها له كتلة وسرعة . وتتناسب متوسط طاقة الحركة لجميع الجسيمات تناسبا طرديا مع درجة الحرارة.
حيث متوسط مربع سرعة الجسيمات ، وkB ثابت بولتزمان.
ومنها نرى أن الجزيئات تتحرك بسرعات كبيرة عندما تكون درجة حرارة الغاز عالية. تفعل ذلك فلا تكون سرعاتها متساوية ، وإنما تتبع السرعات توزيعا احصائيا منتظما، ويسمى هذا التوزيع توزيع ماكسويل-بولتزمان.
فإذا كان الغاز موجودا في وعاء حجمه تصتدم جزيئات الغاز باستمرار بجدار الوعاء وترتد منه. بذلك تعطي الجزيئات بعضا من زخم حركتها ، وتعطي الجزيئات جزءا من زخم حركتها للجدار في كل ثانية على كل سنتيمتر مربع من سطح الجدار. وتؤثر صدمات الجزيئات على كل جزء من أجراء جدار بقوة نسميها "ضغط الغاز" .
- = .
ويكون ذلك الضغط كبيرا كلما زادت سرعة الجسيمات. فمن ناحية يزداد معدل اصتدام الجزيئات بالجدار بزيادة سرعة الجزيئات ، ومن جهة أخرى تكون الصدمات أكثر شدة بزيادة السرعة و يزداد جزء زخم الحركة الذي تعطيه الجزيئات إلى الجدار . فإذا زادت كثافة الجزيئات في الغاز يزيد احتمال اصتدام الجزيئات بالجدار . من ذلك يمكن استنباط معادة الضغط للغاز:
- .
وإذا عوضنا عن متوسط طاقة الحركة للجزيئات بدرجة الحرارة ، نحصل على معادلة اغاز المثالي :
- .
تنطبق تلك المعادلة على غازات قليلة الكثافة وعند درجة حرارة عالية. وعند استنباطنا لها فقد أهملنا قوي التجاذب بين الجسيمات ، التي تخفض من ضغط الجسيمات على جدار الوعاء. وفوق ذلك فإن الجزيئات لها حجم ولا يمكن للغاز أن ينكمش إلى ما لانهاية لأن الجزيئات تشغل جزء من الحجم. أما وصف حالة غاز حقيقي فيمكن بتطبيق معادلة فان دير فال.
ملحوظة: في المعادلة أعلاه التي تعطي متوسط طاقة الحركة للجزيئات نجد فيها العدد 3 في البسط. هذا العدد يعطي ما يسمى درجة حرية الجزيئ ، أي أن في المعادلة توجد "3 درجات حرية" لكل جزيئ ، ذلك يعبر عن أن سرعة v كل جزيئ يمكن تحليلها في ثلاثة اتجاهات : س وص ، ع.
مبدأ أڤوگادرو: ينص على ان الحجوم المتساوية من الغازات المختلفه تحتوي العدد نفسه من الجسيمات عند نفس درجه الحراره والضغط.
ميكانيكا إحصائية
where the first equality is Newton's second law, and the second line uses Hamilton's equations and the equipartition theorem. Summing over a system of N particles yields
the divergence theorem implies that
where dV is an infinitesimal volume within the container and V is the total volume of the container.
Putting these equalities together yields
which immediately implies the ideal gas law for N particles:
حيث n = N/NA عدد مولات الغاز وR = NAkB هي ثابت الغاز.
انظر أيضاً
المصادر
- ^ Clapeyron, E. (1834). "Mémoire sur la puissance motrice de la chaleur". Journal de l'École Polytechnique (in الفرنسية). XIV: 153–90. Facsimile at the Bibliothèque nationale de France (pp. 153–90).
- ^ Moran; Shapiro (2000). Fundamentals of Engineering Thermodynamics (4th ed.). Wiley. ISBN 0-471-31713-6.
- ^ Raymond, Kenneth W. (2010). General, organic, and biological chemistry : an integrated approach (3rd ed.). John Wiley & Sons. p. 186. ISBN 9780470504765. Retrieved 29 January 2019.
قراءات إضافية
- Davis; Masten (2002). Principles of Environmental Engineering and Science. New York: McGraw-Hill. ISBN 0-07-235053-9.
وصلات خارجية
- "Website giving credit to Benoît Paul Émile Clapeyron, (1799–1864) in 1834". Archived from the original on July 5, 2007.
- Configuration integral (statistical mechanics) where an alternative statistical mechanics derivation of the ideal-gas law, using the relationship between the Helmholtz free energy and the partition function, but without using the equipartition theorem, is provided. Vu-Quoc, L., Configuration integral (statistical mechanics), 2008. this wiki site is down; see this article in the web archive on 2012 April 28.
- pv=nrt calculator Engineering Units online calculator