ميكانيكا الاستمرارية
| جزء من سلسلة عن |
| ميكانيكا الاستمرارية |
|---|
ميكانيكا الاستمرارية (Continuum mechanics)، أحد فروع الميكانيكا، الذي يتعامل مع تشوه القوى ونقلها عبر المواد المنمذجة على أنها وسط مستمر (وتسمى أيضًا استمرارية) وليس على أنها جسيمات منفصلة. كان عالم الرياضيات الفرنسي أوگوستان-لوي كوشي أول من صاغ مثل هذه النماذج في القرن التاسع عشر.
تتعامل ميكانيكا الاستمرارية مع "الأجسام القابلة للتشوه"، على عكس الأجسام الجاسئة. يفترض النموذج الاستمراري أن مادة الجسم تملأ المساحة التي تشغلها بالكامل. وبينما يتجاهل حقيقة أن المادة تتكون من ذرات، فإن هذا يوفر وصفًا دقيقًا بدرجة كافية للمادة على مقاييس طول أكبر بكثير من مسافات بين الذرات. يسمح مفهوم الوسط المستمر بالتحليل البديهي للمادة السائبة باستخدام المعادلات التفاضلية التي تصف سلوك هذه المادة وفقًا للقوانين الفيزيائية، مثل حفظ الكتلة، وحفظ الزخم، وحفظ الطاقة. يتم التعبير عن المعلومات حول المادة المحددة في العلاقات التكوينية.
تتعامل ميكانيكا الاستمرارية مع الخصائص الفيزيائية للمواد الصلبة والسوائل بشكل مستقل عن أي نظام إحداثيات معين يتم ملاحظتها فيه. ت/ُل هذه الخصائص بواسطة الموتر، وهي كائنات رياضية لها الخاصية البارزة المتمثلة في كونها مستقلة عن أنظمة الإحداثيات. يسمح هذا بتعريف الخصائص الفيزيائية في أي نقطة في المتصل، وفقًا لدالة مستمرة ملائمة رياضيًا. تستند نظريات المرونة واللدونة وميكانيكا الموائع على مفاهيم ميكانيكا الاستمرارية.
مفهوم الاستمرارية
The concept of a continuum underlies the mathematical framework for studying large-scale forces and deformations in materials. Although materials are composed of discrete atoms and molecules, separated by empty space or microscopic cracks and crystallographic defects, physical phenomena can often be modeled by considering a substance distributed throughout some region of space. A continuum is a body that can be continually sub-divided into infinitesimal elements with local material properties defined at any particular point. Properties of the bulk material can therefore be described by continuous functions, and their evolution can be studied using the mathematics of calculus.
Apart from the assumption of continuity, two other independent assumptions are often employed in the study of continuum mechanics. These are homogeneity (assumption of identical properties at all locations) and isotropy (assumption of directionally invariant vector properties).[1] If these auxiliary assumptions are not globally applicable, the material may be segregated into sections where they are applicable in order to simplify the analysis. For more complex cases, one or both of these assumptions can be dropped. In these cases, computational methods are often used to solve the differential equations describing the evolution of material properties.
المجالات الرئيسية
| ميكانيكا الاستمرارية دراسة فيزياء مواد الاستمرارية |
ميكانيكا المواد الصلبة دراسة فيزياء المواد المستمرة ذات شكل السكون المحدد. |
المرونة تصف المواد التي تعود لحالة سكونها بعد إزالة الإجهاد المطلبق. | |
| اللدونة تصف المواد التي تنفعل بشكل دائم بعد تطبيق الإجهاد الكافي. |
ريولوجيا دراسة المواد ذات الخصائص الصلبة والمائعة. | ||
| ميكانيكا الموائع دراسة فيزياء المواد المستمرة التي تنفعل عندما تخضع لقوة. |
الموائع اللانيوتنية لا تخضع لمعدلات ضغط تتناسب مع الإجهاد المطبق. | ||
| الموائع النيوتنية تخضع لمعدلات ضغط تتناسب مع الإجهاد المطبق. | |||
An additional area of continuum mechanics comprises elastomeric foams, which exhibit a curious hyperbolic stress-strain relationship. The elastomer is a true continuum, but a homogeneous distribution of voids gives it unusual properties.[2]
صياغة النماذج
Continuum mechanics models begin by assigning a region in three-dimensional Euclidean space to the material body being modeled. The points within this region are called particles or material points. Different configurations or states of the body correspond to different regions in Euclidean space. The region corresponding to the body's configuration at time is labeled .
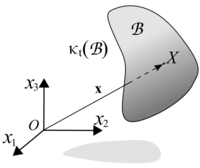
A particular particle within the body in a particular configuration is characterized by a position vector
where are the coordinate vectors in some frame of reference chosen for the problem (See figure 1). This vector can be expressed as a function of the particle position in some reference configuration, for example the configuration at the initial time, so that
This function needs to have various properties so that the model makes physical sense. needs to be:
- continuous in time, so that the body changes in a way which is realistic,
- globally invertible at all times, so that the body cannot intersect itself,
- orientation-preserving, as transformations which produce mirror reflections are not possible in nature.
For the mathematical formulation of the model, is also assumed to be twice continuously differentiable, so that differential equations describing the motion may be formulated.
القوى في استمرارية
A solid is a deformable body that possesses shear strength, sc. a solid can support shear forces (forces parallel to the material surface on which they act). Fluids, on the other hand, do not sustain shear forces.
Following the classical dynamics of Newton and Euler, the motion of a material body is produced by the action of externally applied forces which are assumed to be of two kinds: surface forces and body forces .[3] Thus, the total force applied to a body or to a portion of the body can be expressed as:
القوى السطحية
Surface forces or contact forces, expressed as force per unit area, can act either on the bounding surface of the body, as a result of mechanical contact with other bodies, or on imaginary internal surfaces that bound portions of the body, as a result of the mechanical interaction between the parts of the body to either side of the surface (Euler-Cauchy's stress principle). When a body is acted upon by external contact forces, internal contact forces are then transmitted from point to point inside the body to balance their action, according to Newton's third law of motion of conservation of linear momentum and angular momentum (for continuous bodies these laws are called the Euler's equations of motion). The internal contact forces are related to the body's deformation through constitutive equations. The internal contact forces may be mathematically described by how they relate to the motion of the body, independent of the body's material makeup.[بحاجة لمصدر]
The distribution of internal contact forces throughout the volume of the body is assumed to be continuous. Therefore, there exists a contact force density or Cauchy traction field[4] that represents this distribution in a particular configuration of the body at a given time . It is not a vector field because it depends not only on the position of a particular material point, but also on the local orientation of the surface element as defined by its normal vector .[5][صفحة مطلوبة]
Any differential area with normal vector of a given internal surface area , bounding a portion of the body, experiences a contact force arising from the contact between both portions of the body on each side of , and it is given by
where is the surface traction,[6] also called stress vector,[7] traction,[8][صفحة مطلوبة] or traction vector.[9] The stress vector is a frame-indifferent vector (see Euler-Cauchy's stress principle).
The total contact force on the particular internal surface is then expressed as the sum (surface integral) of the contact forces on all differential surfaces :
In continuum mechanics a body is considered stress-free if the only forces present are those inter-atomic forces (ionic, metallic, and van der Waals forces) required to hold the body together and to keep its shape in the absence of all external influences, including gravitational attraction.[9][10] Stresses generated during manufacture of the body to a specific configuration are also excluded when considering stresses in a body. Therefore, the stresses considered in continuum mechanics are only those produced by deformation of the body, sc. only relative changes in stress are considered, not the absolute values of stress.
قوى الجسم
Body forces are forces originating from sources outside of the body[11] that act on the volume (or mass) of the body. Saying that body forces are due to outside sources implies that the interaction between different parts of the body (internal forces) are manifested through the contact forces alone.[6] These forces arise from the presence of the body in force fields, e.g. gravitational field (gravitational forces) or electromagnetic field (electromagnetic forces), or from inertial forces when bodies are in motion. As the mass of a continuous body is assumed to be continuously distributed, any force originating from the mass is also continuously distributed. Thus, body forces are specified by vector fields which are assumed to be continuous over the entire volume of the body,[12] i.e. acting on every point in it. Body forces are represented by a body force density (per unit of mass), which is a frame-indifferent vector field.
In the case of gravitational forces, the intensity of the force depends on, or is proportional to, the mass density of the material, and it is specified in terms of force per unit mass () or per unit volume (). These two specifications are related through the material density by the equation . Similarly, the intensity of electromagnetic forces depends upon the strength (electric charge) of the electromagnetic field.
The total body force applied to a continuous body is expressed as
Body forces and contact forces acting on the body lead to corresponding moments of force (torques) relative to a given point. Thus, the total applied torque about the origin is given by
In certain situations, not commonly considered in the analysis of the mechanical behavior of materials, it becomes necessary to include two other types of forces: these are couple stresses[note 1][note 2] (surface couples,[11] contact torques)[12] and body moments. Couple stresses are moments per unit area applied on a surface. Body moments, or body couples, are moments per unit volume or per unit mass applied to the volume of the body. Both are important in the analysis of stress for a polarized dielectric solid under the action of an electric field, materials where the molecular structure is taken into consideration (e.g. bones), solids under the action of an external magnetic field, and the dislocation theory of metals.[7][8][صفحة مطلوبة][11]
Materials that exhibit body couples and couple stresses in addition to moments produced exclusively by forces are called polar materials.[8][صفحة مطلوبة][12] Non-polar materials are then those materials with only moments of forces. In the classical branches of continuum mechanics the development of the theory of stresses is based on non-polar materials.
Thus, the sum of all applied forces and torques (with respect to the origin of the coordinate system) in the body can be given by
Kinematics: motion and deformation
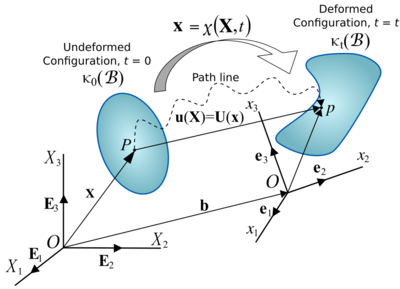
A change in the configuration of a continuum body results in a displacement. The displacement of a body has two components: a rigid-body displacement and a deformation. A rigid-body displacement consists of a simultaneous translation and rotation of the body without changing its shape or size. Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration to a current or deformed configuration (Figure 2).
The motion of a continuum body is a continuous time sequence of displacements. Thus, the material body will occupy different configurations at different times so that a particle occupies a series of points in space which describe a path line.
There is continuity during motion or deformation of a continuum body in the sense that:
- The material points forming a closed curve at any instant will always form a closed curve at any subsequent time.
- The material points forming a closed surface at any instant will always form a closed surface at any subsequent time and the matter within the closed surface will always remain within.
It is convenient to identify a reference configuration or initial condition which all subsequent configurations are referenced from. The reference configuration need not be one that the body will ever occupy. Often, the configuration at is considered the reference configuration, . The components of the position vector of a particle, taken with respect to the reference configuration, are called the material or reference coordinates.
When analyzing the motion or deformation of solids, or the flow of fluids, it is necessary to describe the sequence or evolution of configurations throughout time. One description for motion is made in terms of the material or referential coordinates, called material description or Lagrangian description.
Lagrangian description
In the Lagrangian description the position and physical properties of the particles are described in terms of the material or referential coordinates and time. In this case the reference configuration is the configuration at . An observer standing in the frame of reference observes the changes in the position and physical properties as the material body moves in space as time progresses. The results obtained are independent of the choice of initial time and reference configuration, . This description is normally used in solid mechanics.
In the Lagrangian description, the motion of a continuum body is expressed by the mapping function (Figure 2),
which is a mapping of the initial configuration onto the current configuration , giving a geometrical correspondence between them, i.e. giving the position vector that a particle , with a position vector in the undeformed or reference configuration , will occupy in the current or deformed configuration at time . The components are called the spatial coordinates.
Physical and kinematic properties , i.e. thermodynamic properties and flow velocity, which describe or characterize features of the material body, are expressed as continuous functions of position and time, i.e. .
The material derivative of any property of a continuum, which may be a scalar, vector, or tensor, is the time rate of change of that property for a specific group of particles of the moving continuum body. The material derivative is also known as the substantial derivative, or comoving derivative, or convective derivative. It can be thought as the rate at which the property changes when measured by an observer traveling with that group of particles.
In the Lagrangian description, the material derivative of is simply the partial derivative with respect to time, and the position vector is held constant as it does not change with time. Thus, we have
The instantaneous position is a property of a particle, and its material derivative is the instantaneous flow velocity of the particle. Therefore, the flow velocity field of the continuum is given by
Similarly, the acceleration field is given by
Continuity in the Lagrangian description is expressed by the spatial and temporal continuity of the mapping from the reference configuration to the current configuration of the material points. All physical quantities characterizing the continuum are described this way. In this sense, the function and are single-valued and continuous, with continuous derivatives with respect to space and time to whatever order is required, usually to the second or third.
Eulerian description
Continuity allows for the inverse of to trace backwards where the particle currently located at was located in the initial or referenced configuration . In this case the description of motion is made in terms of the spatial coordinates, in which case is called the spatial description or Eulerian description, i.e. the current configuration is taken as the reference configuration.
The Eulerian description, introduced by d'Alembert, focuses on the current configuration , giving attention to what is occurring at a fixed point in space as time progresses, instead of giving attention to individual particles as they move through space and time. This approach is conveniently applied in the study of fluid flow where the kinematic property of greatest interest is the rate at which change is taking place rather than the shape of the body of fluid at a reference time.[14]
Mathematically, the motion of a continuum using the Eulerian description is expressed by the mapping function
which provides a tracing of the particle which now occupies the position in the current configuration to its original position in the initial configuration .
A necessary and sufficient condition for this inverse function to exist is that the determinant of the Jacobian matrix, often referred to simply as the Jacobian, should be different from zero. Thus,
In the Eulerian description, the physical properties are expressed as
where the functional form of in the Lagrangian description is not the same as the form of in the Eulerian description.
The material derivative of , using the chain rule, is then
The first term on the right-hand side of this equation gives the local rate of change of the property occurring at position . The second term of the right-hand side is the convective rate of change and expresses the contribution of the particle changing position in space (motion).
Continuity in the Eulerian description is expressed by the spatial and temporal continuity and continuous differentiability of the flow velocity field. All physical quantities are defined this way at each instant of time, in the current configuration, as a function of the vector position .
Displacement field
The vector joining the positions of a particle in the undeformed configuration and deformed configuration is called the displacement vector , in the Lagrangian description, or , in the Eulerian description.
A displacement field is a vector field of all displacement vectors for all particles in the body, which relates the deformed configuration with the undeformed configuration. It is convenient to do the analysis of deformation or motion of a continuum body in terms of the displacement field, In general, the displacement field is expressed in terms of the material coordinates as
or in terms of the spatial coordinates as
where are the direction cosines between the material and spatial coordinate systems with unit vectors and , respectively. Thus
and the relationship between and is then given by
Knowing that
then
It is common to superimpose the coordinate systems for the undeformed and deformed configurations, which results in , and the direction cosines become Kronecker deltas, i.e.
Thus, we have
or in terms of the spatial coordinates as
Governing equations
Continuum mechanics deals with the behavior of materials that can be approximated as continuous for certain length and time scales. The equations that govern the mechanics of such materials include the balance laws for mass, momentum, and energy. Kinematic relations and constitutive equations are needed to complete the system of governing equations. Physical restrictions on the form of the constitutive relations can be applied by requiring that the second law of thermodynamics be satisfied under all conditions. In the continuum mechanics of solids, the second law of thermodynamics is satisfied if the Clausius–Duhem form of the entropy inequality is satisfied.
The balance laws express the idea that the rate of change of a quantity (mass, momentum, energy) in a volume must arise from three causes:
- the physical quantity itself flows through the surface that bounds the volume,
- there is a source of the physical quantity on the surface of the volume, or/and,
- there is a source of the physical quantity inside the volume.
Let be the body (an open subset of Euclidean space) and let be its surface (the boundary of ).
Let the motion of material points in the body be described by the map
where is the position of a point in the initial configuration and is the location of the same point in the deformed configuration.
The deformation gradient is given by
Balance laws
Let be a physical quantity that is flowing through the body. Let be sources on the surface of the body and let be sources inside the body. Let be the outward unit normal to the surface . Let be the flow velocity of the physical particles that carry the physical quantity that is flowing. Also, let the speed at which the bounding surface is moving be (in the direction ).
Then, balance laws can be expressed in the general form
The functions , , and can be scalar valued, vector valued, or tensor valued - depending on the physical quantity that the balance equation deals with. If there are internal boundaries in the body, jump discontinuities also need to be specified in the balance laws.
If we take the Eulerian point of view, it can be shown that the balance laws of mass, momentum, and energy for a solid can be written as (assuming the source term is zero for the mass and angular momentum equations)
In the above equations is the mass density (current), is the material time derivative of , is the particle velocity, is the material time derivative of , is the Cauchy stress tensor, is the body force density, is the internal energy per unit mass, is the material time derivative of , is the heat flux vector, and is an energy source per unit mass. The operators used are defined below.
With respect to the reference configuration (the Lagrangian point of view), the balance laws can be written as
In the above, is the first Piola-Kirchhoff stress tensor, and is the mass density in the reference configuration. The first Piola-Kirchhoff stress tensor is related to the Cauchy stress tensor by
We can alternatively define the nominal stress tensor which is the transpose of the first Piola-Kirchhoff stress tensor such that
Then the balance laws become
Operators
The operators in the above equations are defined as
where is a vector field, is a second-order tensor field, and are the components of an orthonormal basis in the current configuration. Also,
where is a vector field, is a second-order tensor field, and are the components of an orthonormal basis in the reference configuration.
The inner product is defined as
Clausius–Duhem inequality
The Clausius–Duhem inequality can be used to express the second law of thermodynamics for elastic-plastic materials. This inequality is a statement concerning the irreversibility of natural processes, especially when energy dissipation is involved.
Just like in the balance laws in the previous section, we assume that there is a flux of a quantity, a source of the quantity, and an internal density of the quantity per unit mass. The quantity of interest in this case is the entropy. Thus, we assume that there is an entropy flux, an entropy source, an internal mass density and an internal specific entropy (i.e. entropy per unit mass) in the region of interest.
Let be such a region and let be its boundary. Then the second law of thermodynamics states that the rate of increase of in this region is greater than or equal to the sum of that supplied to (as a flux or from internal sources) and the change of the internal entropy density due to material flowing in and out of the region.
Let move with a flow velocity and let particles inside have velocities . Let be the unit outward normal to the surface . Let be the density of matter in the region, be the entropy flux at the surface, and be the entropy source per unit mass. Then the entropy inequality may be written as
The scalar entropy flux can be related to the vector flux at the surface by the relation . Under the assumption of incrementally isothermal conditions, we have
where is the heat flux vector, is an energy source per unit mass, and is the absolute temperature of a material point at at time .
We then have the Clausius–Duhem inequality in integral form:
We can show that the entropy inequality may be written in differential form as
In terms of the Cauchy stress and the internal energy, the Clausius–Duhem inequality may be written as
Validity
The validity of the continuum assumption may be verified by a theoretical analysis, in which either some clear periodicity is identified or statistical homogeneity and ergodicity of the microstructure exist. More specifically, the continuum hypothesis hinges on the concepts of a representative elementary volume and separation of scales based on the Hill–Mandel condition. This condition provides a link between an experimentalist's and a theoretician's viewpoint on constitutive equations (linear and nonlinear elastic/inelastic or coupled fields) as well as a way of spatial and statistical averaging of the microstructure. When the separation of scales does not hold, or when one wants to establish a continuum of a finer resolution than the size of the representative volume element (RVE), a statistical volume element (SVE) is employed, which results in random continuum fields. The latter then provide a micromechanics basis for stochastic finite elements (SFE). The levels of SVE and RVE link continuum mechanics to statistical mechanics. Experimentally, the RVE can only be evaluated when the constitutive response is spatially homogenous.
التطبيقات
انظر أيضاً
- مبدأ برنولي
- مادة كوتشي المرنة
- Transport phenomena
- Cauchy elastic material
- Configurational mechanics
- Curvilinear coordinates
- Equation of state
- Finite deformation tensors
- Finite strain theory
- Hyperelastic material
- Lagrangian and Eulerian specification of the flow field
- Movable cellular automaton
- Peridynamics (a non-local continuum theory leading to integral equations)
- Stress (physics)
- Stress measures
- Tensor calculus
- Tensor derivative (continuum mechanics)
- Theory of elasticity
- Knudsen number
ملاحظات
- ^ Maxwell pointed out that nonvanishing body moments exist in a magnet in a magnetic field and in a dielectric material in an electric field with different planes of polarization.[13]
- ^ Couple stresses and body couples were first explored by Voigt and Cosserat, and later reintroduced by Mindlin in 1960 on his work for Bell Labs on pure quartz crystals.[بحاجة لمصدر]
المصادر
الهوامش
- ^ Malvern 1969, p. 2.
- ^ Dienes & Solem 1999, pp. 155–162.
- ^ Smith 1993, p. 97.
- ^ Smith 1993.
- ^ Lubliner 2008.
- ^ أ ب Liu 2002.
- ^ أ ب Wu 2004.
- ^ أ ب ت Fung 1977.
- ^ أ ب Mase 1970.
- ^ Atanackovic & Guran 2000.
- ^ أ ب ت Irgens 2008.
- ^ أ ب ت Chadwick 1999.
- ^ Fung 1977, p. 76.
- ^ Spencer 1980, p. 83.
أعمال مرجعية
- Atanackovic, Teodor M.; Guran, Ardeshir (16 June 2000). Theory of Elasticity for Scientists and Engineers. Dover books on physics (in الإنجليزية). Springer Science & Business Media. ISBN 978-0-8176-4072-9.
- Chadwick, Peter (1 January 1999). Continuum Mechanics: Concise Theory and Problems (in الإنجليزية). Courier Corporation. ISBN 978-0-486-40180-5.
- Dienes, J. K.; Solem, J. C. (1999). "Nonlinear behavior of some hydrostatically stressed isotropic elastomeric foams". Acta Mechanica. 138 (3–4): 155–162. doi:10.1007/BF01291841. S2CID 120320672.
- Fung, Y. C. (1977). A First Course in Continuum Mechanics (2nd ed.). Prentice-Hall, Inc. ISBN 978-0-13-318311-5.
- Irgens, Fridtjov (10 January 2008). Continuum Mechanics (in الإنجليزية). Springer Science & Business Media. ISBN 978-3-540-74298-2.
- Liu, I-Shih (28 May 2002). Continuum Mechanics (in الإنجليزية). Springer Science & Business Media. ISBN 978-3-540-43019-3.
- Lubliner, Jacob (2008). Plasticity Theory (PDF) (Revised ed.). Dover Publications. ISBN 978-0-486-46290-5. Archived from the original (PDF) on 31 March 2010.
- Ostoja-Starzewski, M. (2008). "7-10". Microstructural randomness and scaling in mechanics of materials. CRC Press. ISBN 978-1-58488-417-0.
- Spencer, A. J. M. (1980). Continuum Mechanics. Longman Group Limited (London). p. 83. ISBN 978-0-582-44282-5.
- Roberts, A. J. (1994). A One-Dimensional Introduction to Continuum Mechanics. World Scientific.
- Smith, Donald R. (1993). "2". An introduction to continuum mechanics-after Truesdell and Noll. Solids mechanics and its applications. Vol. 22. Springer Science & Business Media. ISBN 978-90-481-4314-6.
- Wu, Han-Chin (20 December 2004). Continuum Mechanics and Plasticity (in الإنجليزية). Taylor & Francis. ISBN 978-1-58488-363-0.
مصادر عامة
- Batra, R. C. (2006). Elements of Continuum Mechanics. Reston, VA: AIAA.
- Bertram, Albrecht (2012). Elasticity and Plasticity of Large Deformations - An Introduction (Third ed.). Springer. doi:10.1007/978-3-642-24615-9. ISBN 978-3-642-24615-9. S2CID 116496103.
- Chandramouli, P.N (2014). Continuum Mechanics. Yes Dee Publishing Pvt Ltd. ISBN 9789380381398. Archived from the original on 4 August 2018. Retrieved 24 March 2014.
- Eringen, A. Cemal (1980). Mechanics of Continua (2nd ed.). Krieger Pub Co. ISBN 978-0-88275-663-9.
- Chen, Youping; James D. Lee; Azim Eskandarian (2009). Meshless Methods in Solid Mechanics (First ed.). Springer New York. ISBN 978-1-4419-2148-2.
- Dill, Ellis Harold (2006). Continuum Mechanics: Elasticity, Plasticity, Viscoelasticity. Germany: CRC Press. ISBN 978-0-8493-9779-0.
- Dimitrienko, Yuriy (2011). Nonlinear Continuum Mechanics and Large Inelastic Deformations. Germany: Springer. ISBN 978-94-007-0033-8.
- Hutter, Kolumban; Klaus Jöhnk (2004). Continuum Methods of Physical Modeling. Germany: Springer. ISBN 978-3-540-20619-4.
- Gurtin, M. E. (1981). An Introduction to Continuum Mechanics. New York: Academic Press.
- Lai, W. Michael; David Rubin; Erhard Krempl (1996). Introduction to Continuum Mechanics (3rd ed.). Elsevier, Inc. ISBN 978-0-7506-2894-5. Archived from the original on 6 February 2009.
- Lubarda, Vlado A. (2001). Elastoplasticity Theory. CRC Press. ISBN 978-0-8493-1138-3.
- Malvern, Lawrence E. (1969). Introduction to the mechanics of a continuous medium. New Jersey: Prentice-Hall, Inc.
- Mase, George E. (1970). Continuum Mechanics. McGraw-Hill Professional. ISBN 978-0-07-040663-6.
- Mase, G. Thomas; George E. Mase (1999). Continuum Mechanics for Engineers (Second ed.). CRC Press. ISBN 978-0-8493-1855-9.
- Maugin, G. A. (1999). The Thermomechanics of Nonlinear Irreversible Behaviors: An Introduction. Singapore: World Scientific.
- Nemat-Nasser, Sia (2006). Plasticity: A Treatise on Finite Deformation of Heterogeneous Inelastic Materials. Cambridge: Cambridge University Press. ISBN 978-0-521-83979-2.
- Ostoja-Starzewski, Martin (2008). Microstructural Randomness and Scaling in Mechanics of Materials. Boca Raton, FL: Chapman & Hall/CRC Press. ISBN 978-1-58488-417-0.
- Rees, David (2006). Basic Engineering Plasticity - An Introduction with Engineering and Manufacturing Applications. Butterworth-Heinemann. ISBN 978-0-7506-8025-7.
- Wright, T. W. (2002). The Physics and Mathematics of Adiabatic Shear Bands. Cambridge, UK: Cambridge University Press.
وصلات خارجية
- Articles with unsourced statements from December 2022
- Short description with empty Wikidata description
- Pages using sidebar with the child parameter
- Articles with hatnote templates targeting a nonexistent page
- مقالات بالمعرفة بحاجة لذكر رقم الصفحة بالمصدر from August 2020
- Articles with dead external links from December 2023
- ميكانيكا الاستمرارية
- ميكانيكا كلاسيكية
- الصفحات التي تستخدم تنسيقا مهملا لعلامات الرياضيات











































![{\displaystyle {\frac {d}{dt}}[P_{ij\ldots }(\mathbf {X} ,t)]={\frac {\partial }{\partial t}}[P_{ij\ldots }(\mathbf {X} ,t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d57c030f01fac469178b29d8f47a3774b6759949)






![{\displaystyle P_{ij\ldots }=P_{ij\ldots }(\mathbf {X} ,t)=P_{ij\ldots }[\chi ^{-1}(\mathbf {x} ,t),t]=p_{ij\ldots }(\mathbf {x} ,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8285f8b8ab3d209b5b91d73a3b79e2bc66dcb2cf)


![{\displaystyle {\frac {d}{dt}}[p_{ij\ldots }(\mathbf {x} ,t)]={\frac {\partial }{\partial t}}[p_{ij\ldots }(\mathbf {x} ,t)]+{\frac {\partial }{\partial x_{k}}}[p_{ij\ldots }(\mathbf {x} ,t)]{\frac {dx_{k}}{dt}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbdd352ed75c49c13c7f4b3f4b978ed1a26567a1)



























![{\displaystyle {\cfrac {d}{dt}}\left[\int _{\Omega }f(\mathbf {x} ,t)~{\text{dV}}\right]=\int _{\partial \Omega }f(\mathbf {x} ,t)[u_{n}(\mathbf {x} ,t)-\mathbf {v} (\mathbf {x} ,t)\cdot \mathbf {n} (\mathbf {x} ,t)]~{\text{dA}}+\int _{\partial \Omega }g(\mathbf {x} ,t)~{\text{dA}}+\int _{\Omega }h(\mathbf {x} ,t)~{\text{dV}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80f2a1116281a5feb923a41f01ad7f153f68b64d)




































