أحد عشري الأضلاع

Regular hendecagon
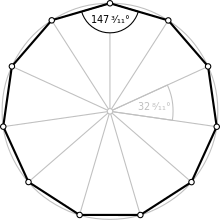A regular hendecagon
النوع	مضلع منتظم
الأضلاع والرؤوس	{{{p11 جانب}}}
رمز شلفلي	{{{p11-شلفلي}}}
مخططات كوكستر-دنكن
مجموعة التماثل	Dihedral (D11), order 2×11
الزاوية الداخلية (الدرجات)	≈147.273°
الخصائص	Convex, cyclic, equilateral, isogonal, isotoxal

في الهندسة الرياضية، الأحادي عشري Hendecagon هو مضلع له 11 ضلع و 11 رأس.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الأحادي العشري المنتظم

• في الأحادي عشري المنتظم يكون قياس الزاوية الداخلية 147.272727... درجة.

• لا يمكن إنشاء الأحادي عشري المنتظم باستخدام إنشاءات الفرجار والمسطرة.

• مساحة الأحادي عشري المنتظم ذو طول ضلع a تعطى بالعلاقة:

$A={\frac {11}{4}}a^{2}\cot {\frac {\pi }{11}}\simeq 9.36564a^{2}.$

 الإنشاء التقريبي

Hendecagon inscribed in a circle, a continuation of the basic construction according to T. Drummond as animation.
Corresponds to the copper engraving by Anton Ernst Burkhard of Birckenstein.

Hendecagon, copper engraving by 1698 by Anton Ernst Burkhard of Birckenstein

The following construction description is given by T. Drummond from 1800:

"Draw the radius A B, bisect it in C—with an opening of the compasses equal to half the radius, upon A and C as centres describe the arcs C D I and A D—with the distance I D upon I describe the arc D O and draw the line C O, which will be the extent of one side of an endecagon sufficiently exact for practice."

On a unit circle:

• Constructed hendecagon side length $b=0.563692\ldots$
• Theoretical hendecagon side length $a=2\sin({\frac {\pi }{11}})=0.563465\ldots$
• Absolute error $\delta =b-a=2.27\ldots \cdot 10^{-4}$ – if AB is 10 m then this error is approximately 2.3 mm.

 التماثل

Symmetries of a regular hendecagon. Vertices are colored by their symmetry positions. Blue mirror lines are drawn through vertices and edge. Gyration orders are given in the center.

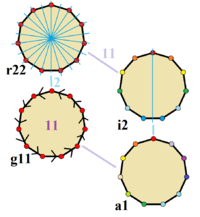
The regular hendecagon has Dih₁₁ symmetry, order 22. Since 11 is a prime number there is one subgroup with dihedral symmetry: Dih₁, and 2 cyclic group symmetries: Z₁₁, and Z₁.

These 4 symmetries can be seen in 4 distinct symmetries on the hendecagon. John Conway labels these by a letter and group order. Full symmetry of the regular form is r22 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g11 subgroup has no degrees of freedom but can seen as directed edges.

 الاستخدام في العملات

The Canadian dollar coin, the loonie, is similar to, but not exactly, a regular hendecagonal prism, as are the Indian 2-rupee coin and several other lesser-used coins of other nations. The cross-section of a loonie is actually a Reuleaux hendecagon. The United States Susan B. Anthony dollar has a hendecagonal outline along the inside of its edges.

 أشكال ذات صلة

The hendecagon shares the same set of 11 vertices with four regular hendecagrams:

{11/2}

{11/3}

{11/4}

{11/5}

 انظر أيضاً

• 10-simplex - can be seen as a complete graph in a regular hendecagonal orthogonal projection

 وصلات خارجية

• Properties of an Undecagon (hendecagon) With interactive animation
• Eric W. Weisstein, Hendecagon at MathWorld.
• Regular hendecagons
• Regular hendecagon, an approximate construction