الحوسبة الكمومية
| جزء من سلسلة مقالات عن |
| ميكانيكا الكم |
|---|
الحاسوب الكمومي Quantum Computer، هو أي وسيلة تستثمر مبادئ ميكانيكا الكم وظواهرها، مثل حالة التراكب الكمومي Quantum Superposition والتشابك الكمومي Quantum Entanglement ، للقيام بمعالجة البيانات.
لا تختلف الحواسيب الكمومية عن الحواسيب المبنية على الترانزستور فقط في التقانة المستخدمة، بل إنها تعتمد نموذجاً آخر للحوسبة غير نمودج آلة تورنگ، وهو نموذج آلة تورنگ الكمومية أو أحياناً يطلق عليها الحاسوب الكمومي الكوني.
في 8 يناير 2019، طرحت آي بي إم أول حاسوب كمومي تجاري، IBM Q System One[1][2][3]
نظرة إجمالية
ليس الشيء المميز في الحواسيب الكمومية هو القدرة الفائقة في التخزين أو المعالجة التقليدية بل إنها القدرة على القيام بعمليات معالجة متوازية، وفي الوقت ذاته.
كل الحواسيب منذ نشوئها، وحتى اليوم تعتمد على النموذج النظري الحاسوبي نفسه، وهو نموذج آلة تورنگالذي يتضمن آلة تقرأ شريطاً مثقباً بشكل متتال، فيمثل الشريط الذاكرة، ويمثل تتابع الثقوب تتابع الأصفار والواحدات، وهذا هو نمط التخزين الثنائي.
تستخدم الحواسيب الكمومية ظواهر غريبة في عالم الفيزياء. هذه الحواسيب ليس بإمكانها فقط تخزين الواحد، أو الصفر، بل تخزين الواحد والصفر في نفس الوقت. لنأخذ بتة عادية. يمكن لهذه البتة أن تخزّن أحد القيمتين: 1 أو 0. أما بالنسبة للبتة الكمومية أو كما تسمى باللغة الإنكليزية Qubit فبإمكانها تخزين الواحد والصفر في الوقت ذاته.
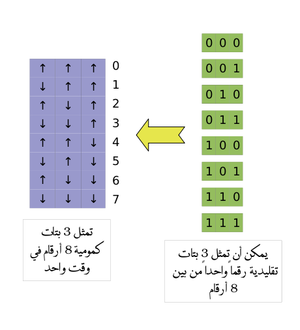
لنأخذ ثلاث بتات عادية. يمكنها تخزين أحد ثماني الأرقام من الصفر إلى السبعة، أما البتة الكمومية فبإمكانها تخزين الأرقام الثماني في الوقت ذاته.
ليس المهم هنا قدرة التخزين الكبيرة. لنحاول أن تتخيل أن هذه البتات الكمومية الثلاثة تستطيع القيام بثماني عمليات في الوقت ذاته، بدل عملية واحدة في الوقت نفسه للبتات العادية. هنا تكمن قوة الحواسيب الكمومية، فقوة المعالجة تزداد بشكل أسي (2^n) بالازدياد الخطي لحجم النظام. هذا الأمر أدى إلى ظهور ما يسمى بالخوارزميات الكمومية والتي تستطيع إنجاز العديد من العمليات الطويلة بزمن قصير.
قد يكون من المفيد الإشارة إلى بعض إمكانات السرعة لإحدى الخوارزميات الكمومية، وهي خوارزمية گروڤر Grover. لنتخيل قاعدة بيانات مؤلفة من مليون سجل. إن عدد العمليات الوسطي لبحث واحد، وباستخدام الوسائل المتاحة، هو نصف مليون عملية، أي n/2. لكن وباستخدام الخوارزمية السابقة فمتوسط العمليات اللازم للقيام ببحث هو جذر n، أي 1000 عملية فقط من أجل مثالنا.
مبادئ التشغيل
يختلف الكمبيوتر الكمومي الذي يحتوي على عدد معين من وحدات البت ، بشكل أساسي عن جهاز كمبيوتر كلاسيكي يتكون من نفس عدد وحدات البت الكلاسيكية. على سبيل المثال ، يتطلب تمثيل حالة نظام n - qubit على كمبيوتر كلاسيكي تخزين 2 n عقدي ، أثناء توصيفه حالة النظام الكلاسيكي n - بت يكفي لتوفير قيم الأرقام n ، أي ، فقط الأرقام n . على الرغم من أن هذه الحقيقة قد تشير إلى أن البتات يمكن أن تحتوي على معلومات أضعافا مضاعفة من نظيراتها الكلاسيكية ، يجب توخي الحذر حتى لا نتجاهل حقيقة أن البتات موجودة فقط في تراكب احتمالي لجميع حالاتها . هذا يعني أنه عند قياس الحالة النهائية للرموز ، سيتم العثور عليها فقط في أحد التكوينات المحتملة التي كانت عليها قبل القياس. من الخطأ عمومًا التفكير في نظام البتات في حالة معينة قبل القياس. منذ حقيقة أنهم كانوا في تراكب الحالات قبل إجراء القياس يؤثر بشكل مباشر على النتائج المحتملة للحساب.

لفهم هذه النقطة بشكل أفضل ، ضع في اعتبارك كمبيوترًا كلاسيكيًا يعمل على امسجل ثلاثة بت . إذا كانت الحالة المحددة للسجل في وقت معين غير معروفة ، فيمكن وصفها على أنها توزيع الاحتمالات على السلاسل المختلفة الثلاثة <بت> 000 ، 001 ، 010 و 011 و 100 و 101 و 110 و و 111 . إذا لم تكن هناك حالة عدم يقين بشأن حالتها ، فستكون في واحدة من هذه الحالات تمامًا مع الاحتمال 1. ومع ذلك ، إذا كان كمبيوتر احتمالي ، فعندئذ تكون هناك إمكانية لوجودها في أي " "واحد" لعدد من الحالات المختلفة. وبالمثل ، يتم وصف حالة الكمبيوتر الكمومي بمقدار ثلاثة كيلو بايت بواسطة ناقل الاتجاه الثنائي الأبعاد (أو متجه واحد الأبعاد مع كل عقدة متجه تحمل السعة والحالة كسلسلة بت من وحدات البت). هنا ، ومع ذلك ، فإن المعاملات هي رقم عقدي مركب ، وهي مجموع "المربعات" للمعاملات " القيم المطلقة, , والتي يجب أن تساوي 1.لكل , القيمة المطلقة المربعة يعطي احتمال وجود النظام في -th الحالة بعد القياس. ومع ذلك ، نظرًا لأن الرقم المركب لا يشفر فقط الحجم ولكن أيضًا الاتجاه في المستوى المركب ، يمثل فرق الطور بين أي معاملتين (حالات) بارامتر ذو معنى. هذا هو الفرق الأساسي بين الحوسبة الكمومية والحوسبة الكلاسيكية الاحتمالية.[5]
إذا قمت بقياس الكيوبتات الثلاثة ، فستلاحظ سلسلة من ثلاثة بتات. إن احتمالية قياس سلسلة معينة هي الحجم التربيعي لمعامل تلك السلسلة (بمعنى ، احتمال القياس 000 = , احتمال القياس 001 = , etc.). Thus, measuring a quantum state described بواسطة معاملات مركبة يعطي توزيع الاحتمال الكلاسيكي ونقول أن الحالة الكمومية "تنهار" إلى الحالة الكلاسيكية نتيجة إجراء القياس. لشرح كيفية "انهيار" الحالة الكمومية إلى حالة كلاسيكية ، دعونا نفكر في مشكلة رياضية تسمى لعبة التبديل الخفيفة [1] ] ، وهذا يوضح لماذا الحوسبة الكمومية هي أكثر كفاءة في حل بعض المشاكل يمكن تحديد متجه ثلاثي الأبعاد بعدة طرق مختلفة اعتمادًا على | الأساس) الذي يتم اختياره للمساحة. أساس سلاسل البت(e.g., 000, 001, …, 111) المعروف باسم الأساس الحسابي. القواعد المحتملة الأخرى هي طول الوحدة ، المتعامد والمتجهات الذاتية لعامل مشغل باولي- x. غالبًا ما يستخدم Ket notation لجعل اختيار الأساس صريحًا. على سبيل المثال ، الحالة في الأساس الحسابي يمكن كتابته كـ:
- حيث مثلاً
الأساس الحسابي ل qubit واحد (ببعدين) هو و .
باستخدام متغيرات eigenvector للعامل Pauli-x ، يكون الكيوبت الواحد و .
التشغيل
في حين أن الحالة الكلاسيكية 3 بت والحالة الكمومية 3 qubit تكون كل منها ثنائية الأبعاد أشعة ، إلا أنهما يتم معالجتهما بطريقة مختلفة تمامًا عن الحساب الكلاسيكي أو الكمومي. للحوسبة في كلتا الحالتين ، يجب تهيئة النظام ، على سبيل المثال في سلسلة الأصفار ، , المقابلة للأشعة (1,0,0,0,0,0,0,0). في الحساب العشوائي الكلاسيكي ، يتطور النظام وفقًا لتطبيق مصفوفات ستوكاستيك ، والتي تحافظ على أن الاحتمالات تضيف ما يصل إلى واحد (أي الحفاظ على L1 norm). في العمليات الحسابية الكمومية ، من ناحية أخرى ، فإن العمليات المسموح بها هي المصفوفات الواحدية ، والتي تدور فعليًا (تحافظ على أن مجموع المربعات يضيف ما يصل إلى واحد ، الإقليدية أو L2 ). ( ما هي الوحدات التي يمكن تطبيقها بالضبط و التي تعتمد على فيزياء الجهاز الكم.) وبالتالي ، بما أن الدورات يمكن التراجع عنها بالتناوب للخلف ، فإن الحسابات الكمومية عكسية. (من الناحية التقنية ، يمكن أن تكون العمليات الكمية عبارة عن مجموعات احتمالية من الواحدات ، لذا فإن حساب الكم يعمم بالفعل الحساب الكلاسيكي. انظر دائرة الكم للحصول على صيغة أكثر دقة.)
الكيوبت
 مقالة مفصلة: كيوبت
مقالة مفصلة: كيوبت
يستخدم الحاسوب الكمومي بعض الظواهر التي تكاد تكون غامضة من ميكانيكا الكم لتحقيق طفرات هائلة في قدرات المعالجة. حيث تتمتع الآلات الكمومية بقدرات واعدة للتفوق على أكثر الحواسيب الفائقة التي نراها اليوم- أو سنراها مستقبلاً- قدرة.
لكن هذه الآلات لن تقضي على وجود الحواسيب التقليدية، فاستخدام الآلات الكلاسيكية سيظل الحل الأسهل والأكثر توفيراً للتكاليف لمعالجة معظم المشاكل. لكن الحواسيب الكمومية لديها إمكانيات واعدة لتحقيق تقدم بارز في مجالات متنوعة، ابتداءً بعلم المواد، وانتهاءً بأبحاث المستحضرات الدوائية. تقوم الشركات حالياً بتجريب هذه الحواسيب لتطوير أشياء مثل بطاريات أخف وزناً وأكثر فعالية للسيارات الكهربائية، وللمساعدة في تصنيع عقاقير جديدة. [6] يكمن سر القدرات العالية للحواسيب الكمومية في قدرتها على توليد اللبنات الكومية (أو ما يسمى الكيوبتات) والتعامل معها.
تستخدم حواسيب اليوم البتات (وحدة البت) وهي تدفق من النبضات الكهربائية أو الضوئية التي تمثل الوحدان 1 والأصفار 0. فكل شيء من تغريداتك على تويتر، إلى رسالتك الإلكترونية، إلى أغانيك على آيتيونز ومقاطع الفيديو على يوتيوب، كل ذلك هو في الأساس عبارة عن سلاسل طويلة من هذه الأرقام. من الناحية الاخرى، تستخدم الحواسيب الكمومية الكيوبتات، وهي عادة ما تكون جسيمات دون ذرية مثل الإلكترونيات والفوتونات، ويمثل إنتاج وإدارة الكيوبتات تحدياً علمياً وهندسياً. إن بعض الشركات مثل آي بي إم، جوجل، وريجتي كومبيوتينج، تستخدم دارات فائقة الناقلية يتم تبريدها إلى درجات حرارة أشد برودة من الفضاء العميق. في حين تقوم شركات أخرى مثل أيون-كيو، بحصر ذرات منفردة داخل حقول كهرومغناطيسية على شرائح السيليكون داخل حجرات فائقة التفريغ، في كلا الحالتين، فإن الهدف هو عزل الكيوبتات في حالة كمومية مضبوطة. تتمتع الكيوبتات ببعض الخصائص الكمومية غريبة الاطوار، هذا يعني أنه يمكن لمجموعة متصلة منها أن توفر قدرة معالجة أعلى بكثير مما يوفره نفس العدد من البتات الثنائية، إحدى هذه الخصائص تعرف باسم "التراكب"، والخاصية الأخرى تسمى "التشابك".
التراكب الكمي
يمكن للكيوبتات أن تمثل عدداً كبيراً من التركيبات المحتملة من الوحدات 1 أو الأصفار 0 في الوقت نفسه، هذه القدرة على اتخاذ حالات متعددة في الوقت نفسه تسمى بالتراكب. لوضع الكيوبتات في حالة من التراكب، يقوم الباحثون بمعالجتها باستخدام حزمات من أشعة الليزر أو الموجات المكروية.
بفضل هذه الظاهرة غير المنطقية، يمكن للحاسوب الكمومي باستخدام عدة كيوبتات في حالة من التراكب أن يعالج عدداً هائلاً من المخرجات المحتملة بشكل متزامن، لا تظهر النتيجة النهائية للعملية الحسابية إلا بعد أن يتم قياس الكيوبتات، والذي يؤدي على الفور إلى "إنهيار" الحالة الكمومية لتأخذ إما القيمة 1 أو القيمة 0.
التشابك الكمي
يمكن للباحثين أن يولدوا أزواجاً من الكيوبتات "المتشابكة"، ما يعني ان كلا عنصري الزوج الواحد يمكنهما التواجد في حالة كمومية واحدة، حيث أن تغيير حالة أحد الكيوبتين يؤدي على الفور إلى تغير حالة الكيوبت الآخر بطريقة يمكن التنبؤ بها. يحدث هذا الأمر حتى لو كان هناك مسافات شاسعة تفصل بين عناصر الأزواج. لا أحد يعلم حقيقة كيف يجري التشابك أو ما الذي يتسبب بحدوثه، حيث أنه حير أينشتاين الذي اشتهر بوصفه على أنه "عمل شبحي يجري عن بعد". ولكنه ظاهرة أساسية تكمن وراء قوة الحواسيب الكمومية. ففي الحاسوب التقليدي، تؤدي مضاعفة عدد البتات المستخدمة إلى مضاعفة قدرته على المعالجة، ولكن بفضل ظاهرة التشابك، فإن إضافة كيوبتات إضافية إلى آلة كمومية يتسبب بزيادة هائلة في قدرتها على معالجة الأرقام. تستخدم الحواسيب الكمومية الكيوبتات المتشابكة في نوع من السلسلة التعاقبية الكمومية لتقوم بأعمالها السحرية، إن قدرة الآلات على تسريع العمليات الحسابية باستخدام خوارزميات كمومية مصممة بشكل خاص هي السبب في وجود ضجة كبيرة حول إمكانياتها. هذا هو الخبر السار من الامر، أما الخبر السيء، فهو أن هذه الآلات الكمومية أكثر عرضة لارتكاب الأخطاء مقارنة بالحواسيب الكلاسيكية نتيجة زوال الترابط الكمي.
زوال الترابط الكمي
إن تفاعل الكيوبتات مع بيئتها المحيطة بطريق تؤدي إلى تراجع سلوكها الكمومي واختفائه في نهاية المطاف يعرف باسم "زوال الترابط الكمي". فحالتها الكمومية بالغة الحساسية، لأن أقل اهتزاز أو تغير في درجة الحرارة- وهي اضطرابات تعرف باسم "الضجيج" في مصطلحات ميكانيكا الكم- يمكنه أن يتسبب بإخراجها من حالة التراكب قبل أن تنجز عملها بشكل صحيح. هذا ما يدفع الباحثين إلى بذل قصارى جهدهم لحماية الكيوبتات من العالم الخارجي داخل تلك الثلاجات فائقة التبريد والحجرات فائقة التفريغ.
ولكن وعلى الرغم من الجهود التي يبذلونها، لا يزال الضجيج يتسبب بتسلل الكثير من الأخطاء إلى العمليات الحسابية. يمكن لخوارزميات الكم الذكية أن تقوم بعضاً من هذه الأخطاء، كما أن إضافة المزيد من الكيوبتات يلعب دوراً مساعداً أيضاً. مع ذلك، فإنه من المرجح أن يتطلب الامر استخدام الآلاف من الكيوبتات المعيارية لإنشاء كيوبت واحد موثوق للغاية، يعرف باسم "الكيوبت المنطقي". سيؤدي هذا إلى استنزاف الكثير من القدرات الحسابية للحاسوب الكمومي.
وهناك تمكن المشكلة، فحتى الآن، لم يتمكن الباحثون من تمكن أكث رمن 128 كيوبت معياري. لذلك لا يزال أمامنا العديد من السنوات قبل أن نحظى بحواسيب كمومية يمكنها أن تلعب دوراً مجدياً على نطاق واسع.
لكن هذا لم يقلل من آمال رواد هذا المجال في أن يكونوا أول من يبرهن على "التفوق الكمومي".
القدرات
التشفير
فإن عدداً صحيحاً من العوامل ، الذي يدعم أمان أنظمة تشفير المفتاح العام ، غير ممكن حسابيًا مع جهاز كمبيوتر عادي للأعداد الصحيحة الكبيرة إذا كانت نتاج عدد قليل أعداد أولية (على سبيل المثال ، منتجات من 300 رقم أولي).[7] بالمقارنة ، يمكن للكمبيوتر الكمومي حل هذه المشكلة بكفاءة باستخدام خوارزمية Shor للعثور على عواملها. من شأن هذه القدرة أن تسمح لجهاز الكمبيوتر الكمي بتحطيم العديد من التشفيرات المستخدمة اليوم ، بمعنى أنه سيكون هناك متعدد الحدود الزمنية (في عدد الأرقام هنالك عدد صحيح) ل حل مشكلة. على وجه الخصوص ، تعتمد معظم أصفار المفتاح العام على صعوبة تحليل الأعداد الصحيحة أو مشكلة اللوغاريتم المنفصل ، وكلاهما يمكن حلهما بواسطة خوارزمية Shor. على وجه الخصوص ، خوارزميات RSA ، و Diffie-Hellman ، و elliptic curve Diffie-Hellman التي يمكن كسرها. يتم استخدامها لحماية صفحات الويب الآمنة والبريد الإلكتروني المشفر والعديد من أنواع البيانات الأخرى. كسر و اختراق هؤلاء سيكون له تداعيات كبيرة على الخصوصية والأمن الإلكتروني.
البحث الكمومي
إلى جانب التوصيف واللوغاريتمات المنفصلة ، تم العثور على خوارزميات الكم التي تقدم أكثر من تسريع متعدد الحدود على خوارزمية كلاسيكية معروفة لعدة مشاكل,[8] بما في ذلك محاكاة العمليات الفيزيائية الكمومية من الكيمياء وفيزياء الحالة الصلبة ، وتقريب جونز متعدد الحدود ، وحل معادلة بيل. لم يتم العثور على دليل رياضي يوضح أنه لا يمكن اكتشاف خوارزمية كلاسيكية سريعة بنفس القدر ، على الرغم من أن هذا يعتبر غير مرجح.[9]بالنسبة لبعض المشكلات ، تقدم أجهزة الكمبيوتر الكمومية تسريع متعدد الحدود. المثال الأكثر شهرة لهذا هو "البحث في قاعدة البيانات الكمومية" ، والذي يمكن حله بواسطة خوارزمية Grover's باستخدام عدد أقل من الاستعلامات إلى قاعدة البيانات من الناحية التربيعية أقل من تلك المطلوبة بواسطة الخوارزميات الكلاسيكية. في هذه الحالة ، لا تكون الميزة مثبتة فحسب ، بل هي الأمثل أيضًا ، فقد ثبت أن خوارزمية Grover تعطي أقصى احتمال ممكن للعثور على العنصر المطلوب لأي عدد من عمليات البحث عن أوراكل. تم اكتشاف العديد من الأمثلة الأخرى على سرعات الكم التي يمكن إثباتها فيما يتعلق بمشكلات الاستعلام ، مثل العثور على تصادمات في وظائف ثنائية إلى جانب وتقييم تشعبات بوابة NAND.
المحاكاة الكمومية
نظرًا لأن الكيمياء وتقنية النانو تعتمدان على فهم الأنظمة الكمومية ، ومن المستحيل محاكاة هذه النظم بطريقة فعالة من الناحية الكلاسيكية ، يعتقد الكثيرون أن محاكاة الكم ستكون واحدة من أهم تطبيقات الحوسبة الكمومية.[10] يمكن أيضًا استخدام المحاكاة الكمومية لمحاكاة سلوك الذرات والجسيمات في ظروف غير عادية مثل التفاعلات داخل Collider.[11]
التلدين الكمومي والاستمثال الأدياباتي
حساب الكم الأديابي يعتمد على نظرية الأديابيك لإجراء العمليات الحسابية. يتم وضع نظام في الحالة الأساسية لرجل هاميلتون بسيط ، والذي تم تطويره ببطء إلى عامل هاميلتون أكثر تعقيدًا تمثل حالته الأساسية الحل للمشكلة المعنية. تنص نظرية adiabatic على أنه إذا كان التطور بطيئًا بما فيه الكفاية ، فسيبقى النظام في وضعه الأساسي في جميع الأوقات خلال العملية.
حل المعادلات الخطية
من المتوقع أن تقدم خوارزمية الكم للأنظمة الخطية للمعادلات أو "خوارزمية HHL" ، التي سميت على اسم مكتشفاتها Harrow و Hassidim و Lloyd ، تسريعًا على نظرائهم الكلاسيكيين.[12]
تفوق الكمومية
 مقالة مفصلة: تفوق كمومي
مقالة مفصلة: تفوق كمومي
التفوق الكمومي المرحلة التي يمكن فيها للحاسوب الكمومي أن ينجز حساباً رياضياً يثبت أنه يتجاوز قدرات أقوى الحواسيب الفائقة. لا يزال من غير الواضح بالضبط ما هو عد الكيوبتات المطلوب لتحقيق ذلك، لأن الباحثين يوصالون البحث عن خوارزميات جديدة لتعزيز أداء الآلات الكلاسيكية، كما أن المكونات المادية الخاصة بالحوسبة الفائقة مستمرة في التحسن. ولكن الباحثين والشركات يعملون جاهداً لتحقيق اللقب (التفوق الكمومي)، عبر إجراء الاختبارات مقارنة بعدد من أقوى الحواسيب الفائقة في العالم.
هناك الكثير من النقاش الذي يجري في عالم الأبحاث حول مدى أهمية تحقيق هذا الإنجاز. وبدلاً من إنتظار الإعلان عن التفوق، فقد بدأت الشركات في الواقع بإجراء التجارب بإستخدام حواسيب كمومية تم تصنيعها من قبل شركات مثل آي بي إم، ريجيتي، والشركة الكندية دي-ويف، كما أن هناك شركات صينية مثل علي بابا توفر إمكانية الوصول إلى الآلات الكمومية، وتقوم بعض الشركات بشراء الحواسيب الكمومية، في حين تستخدم شركات أخرى الحواسيب الكمومية المتاحة عبر خدمات الحوسبة السحابية.
العقبات
هناك عدد من التحديات التقنية في بناء كمبيوتر كمومي واسع النطاق ، وحتى الآن لم تتمكن أجهزة الكمبيوتر الكمومية من حل مشكلة بشكل أسرع من الكمبيوتر الكلاسيكي. قام David DiVincenzo من IBM ، بإدراج ما يلي المتطلبات للكمبيوتر الكم العملي:[13]* قابلة للتطوير فيزيائياً لزيادة عدد وحدات البت.
- وحدات البت التي يمكن تهيئتها للقيم العشوائية ؛
- البوابات الكمومية التي هي أسرع من زمن decoherence دراسة تفاعلات النظام الكمومي؛
- مجموعة بوابة عالمية.
- وحدات البت التي يمكن قراءتها بسهولة.
التطورات
نماذج الحوسبة الكمومية
هنالك عدد من نماذج الحوسبة الكمومية ، تتميز بالعناصر الأساسية التي يتحلل فيها الحسابة. النماذج الأربعة الرئيسية ذات الأهمية العملية هي:
- مصفوفة بوابة الكم (حساب متحلل في سلسلة قليلة الكويبت بوابة الكم ق)
- كمبيوتر كم وحيد الاتجاه (حساب متحلل في سلسلة من قياسات البايت الواحد المطبقة على حالة أولية متشابكة للغاية أو حالة عنقودية)
- كمبيوتر الكم الأديابي ، استنادًا إلى الدعم الكمي (يتحلل الحساب إلى تحول بطيء مستمر أولي هاملتونيان إلى تابع التشغيل هاملتون نهائي تحتوي حالته الأولية على الحل)[14]
- كمبيوتر الكم الطوبوغرافي[15](حساب متحلل في جدل anyon في شبكة شعرية ثنائية الأبعاد)
تعتبر آلة تورينج الكم مهمة من الناحية النظرية ولكن لم يتم متابعة التنفيذ المباشر لهذا النموذج. جميع النماذج الأربعة للحساب قد تبين أنها متكافئة ؛ يمكن لكل منهما محاكاة الآخر من دون زيادة كثيرات الحدود.
الإنجازات الفيزيائية
من أجل التنفيذ الفعلي لجهاز كمبيوتر كمومي ، يتم متابعة العديد من المرشحين المختلفين ، من بينهم (النظام الذي يتميز بأنه مادي\فيزيائي المستخدم لتحقيق البتات):
- الحوسبة الكمومية ذات الموصلية الفائقة[16][17] ( حالة qubit التي تنفذها الدارات الصغيرة فائقة التوصيل (تقاطعات جوزيفسون))
- الكمبيوتر الكمي ذو الأيونات المحتجزة (حيث يتم تنفيذ الكيوبتات من خلال الحالة الداخلية للأيونات المحتجزة)
- الشبكات البصرية (حيث يتم تنفيذ الكيوبتات من خلال الحالات الداخلية من الذرات المحايدة المحتجزة في الشبكات الشعرية البصرية)
- كمبيوتر Quantum dot ، القائم على الدوران (على سبيل المثال ، كمبيوتر Loss-DiVincenzo[18]) (الكيوبت المعطى هو دوران الكترونات المحتجزة)
- كمبيوتر Quantum dot ، القائم على المكانية أو الفضائية (حيث تعطى الكيوبتات بواسطة موقع الإلكترون في نقطة كمومية مزدوجة)[19]
- سلك الكم المزدوج (حيث يتم تنفيذ الكيوبتات بواسطة زوج من الأسلاك الكمومية إلى جانب جهة اتصال نقطة الكم)[20][21][22]
- كمبيوتر الكم بالرنين المغناطيسي النووي (NMRQC) الذي تم تنفيذه باستخدام الرنين المغناطيسي النووي من الجزيئات في محلول ، حيث يتم توفير البتات بواسطة الدوران النووي داخل الجزيء المذاب والتحقق من الأمواج المرسلة
- الرنين النووي المغناطيسي في الحالة الصلبة الكمبيوتر الكم Kane ( حيث تتحقق الكيوبتات من خلال حالة الدوران النووي لـ الفسفورمن الالكترونات الممنوحة في السيليكون)
- الحواسيب الكمومية ذات الإلكترونات التي تعمل على - الهليوم (الكيوبت هو الإلكترون الدوار)
- الديناميكا الكهربائية التجويفية الكمومية (CQED) (الكيوبت الذي توفره الحالة الداخلية للذرات المحتجزة إلى جانب تجاويف عالية الجودة)
- المغناطيس الجزيئي[23] (يتم تحديد الكيوبت من الحالات الدوارة)
- الكمبيوتر الكمومي Fullerene - المعتمد على ESR الرنين المغنطيسي للإلكترون (يحدد الكيوبت بناءً على الدوران الإلكتروني لـ الذرات أو الجزيئات المغلفة في الفوليرين وهو شكل من أشكال الكربون يحتوي على جزيء كروي كبير يتكون من قفص أجوف من الذرات)
- كمبيوتر الكم البصري الخطي ( يتم تحقيق الكيوبتات من خلال معالجة حالات مختلفة لأوضاع الضوء من خلال عناصر خطية مثل المرايا ، موزع الحزمة و طور الإزاحة)[24]
- كمبيوتر الكم القائم على الماس[25][26][27] ( تتحقق الكيوبت من الدوران الإلكتروني أو النووي لـ مركز الفراغ النيتروجيني في الماس)
- كومبيوتر الكم القائم على Bose-Einstein condensate [28]
- الكمبيوتر الكمومي القائم على الترانزستور - سلسلة الكمبيوترات الكمومية مع انجذاب من الثقوب الموجبة باستخدام الحصر الكهربائي
- أجهزة كمبيوتر كمومية غير عضوية المستخلصة بالكريستال النادر[29][30] ( تتحقق الكيوبت من خلال الحالة الإلكترونية الداخلية لـ المحفزات في الألياف الضوئية و الكربونات النانوية التي تشبه المعدن[31]
يوضح عدد كبير من المرشحين أن الموضوع ، على الرغم من التقدم السريع ، لا يزال في بدايته. فهناك أيضًا قدر كبير من الجهود المشتركة و التعاون في العمل.
خط زمني
1905: Albert Einstein explains the photoelectric effect and suggests that light consists of quantum particles or photons
1924: Max Born uses the term quantum mechanics for the first time
1925: Werner Heisenberg, Max Born, and Pascual Jordan formulate matrix mechanics, the first formulation of quantum mechanics
1925-1927: Niels Bohr and Werner Heisenberg develop the Copenhagen interpretation, one of the earliest and most common interpretations of quantum mechanics
1930: Paul Dirac publishes The Principles of Quantum Mechanics, a standard textbook on quantum theory
1935: Albert Einstein, Boris Podolsky, and Nathan Rosen publish a paper highlighting the counterintuitive nature of quantum superposition and arguing that quantum mechanics is incomplete
1935: Erwin Schrödinger develops a thought experiment involving a cat that is simultaneously dead and alive, and coins the term “quantum entanglement”
1944: John von Neumann publishes Mathematical Foundations of Quantum Mechanics, a rigorous mathematical framework for quantum theory
1957: Hugh Everett proposes the many-worlds interpretation of quantum mechanics, which suggests that every possible outcome of a quantum measurement actually occurs in a parallel universe
في عام 1959 ريتشارد فاينمان في محاضرته "هناك الكثير من الفضاء في القاع" تنص على إمكانية استخدام تأثيرات الكم للحساب. في عام 1980 وصف بول Benioff نماذج كم هاميلتون الميكانيكية لأجهزة الكمبيوتر[32] دفع و حفز عالم الرياضيات الروسي يوري مانين من عجلة تطوير أجهزة الكمبيوتر الكمومية.[33]
1961: Rolf Landauer shows that erasing a bit of information dissipates a minimum amount of energy, known as Landauer’s principle
1965: John Bell proves that quantum entanglement cannot be explained by any local hidden variable theory, known as Bell’s theorem
1973: Alexander Holevo proves that n qubits cannot carry more than n classical bits of information, known as Holevo’s theorem or Holevo’s bound
1980: Paul Benioff proposes a model of a quantum Turing machine, a theoretical device that can perform any computation using quantum mechanical principles
في عام 1981 ، في مؤتمر اشترك في تنظيمه MIT و IBM ، حث الفيزيائي ريتشارد فاينمان العالم على بناء كمبيوتر كمّي. قال: "الطبيعة ليست كلاسيكية ، اللعنة ، وإذا كنت ترغب في إجراء محاكاة للطبيعة ، فمن الأفضل أن تجعلها ميكانيكية ، ومن الناحية اللطيفة ، إنها مشكلة رائعة لأنها لا تبدو سهلة للغاية."[34]
1982: David Deutsch generalizes Benioff’s model and proposes the concept of a universal quantum computer
في عام 1984 ، تم نشر BB84 ، وهو أول بروتوكول تشفير كمي في العالم من قبل علماء IBM Charles Bennett و Gilles Brassard.
1984: Charles Bennett and Gilles Brassard develop a protocol for quantum key distribution, which allows two parties to securely exchange cryptographic keys using quantum states
1985: David Deutsch and Richard Jozsa devise an algorithm that can solve a specific problem faster than any classical algorithm, known as the Deutsch-Jozsa algorithm
1991: Artur Ekert proposes another protocol for quantum key distribution based on quantum entanglement, known as the E91 protocol
1992: David Deutsch and Richard Jozsa extend their algorithm to handle multiple inputs, known as the Deutsch-Jozsa algorithm
في عام 1993 ، أظهرت مجموعة دولية من ستة علماء ، من بينهم تشارلز بينيت ، أن عملية النقل الكمي عن بعد المثالية ممكنة[35] من حيث المبدأ ، ولكن فقط إذا تم إلغاء أو تدمير الأصل.
في عام 1994 ، اكتشف Peter Shor ، في Bell Labs خوارزمية كمية مهمة ، والتي تسمح للحاسوب الكمي بمعالجة أعداد صحيحة كبيرة بشكل أسرع بكثير من أفضل الخوارزمية الكلاسيكية المعروفة. خوارزمية Shor يمكن نظريًا كسر الكثير من تشفير المفتاح العام المستخدمة اليوم[36]أثار اختراعها اهتماما هائلا في أجهزة كمبيوتر الكم.
1994: Peter Shor discovers an algorithm that can factor large numbers in polynomial time using a quantum computer, known as Shor’s algorithm
1996: Lov Grover invents an algorithm that can search an unsorted database in square root time using a quantum computer, known as Grover’s algorithm
في عام 1996 ، تم نشر معايير DiVincenzo وهي قائمة من الشروط الضرورية لبناء جهاز كمبيوتر كمّي اقترحه الفيزيائي النظري David P. DiVincenzo في بحثه عام 2000 "التنفيذ المادي للحساب الكمومي" ".
1997: Isaac Chuang, Neil Gershenfeld, and Mark Kubinec demonstrate the first implementation of Shor’s algorithm using nuclear magnetic resonance (NMR) techniques
2000: David DiVincenzo proposes five criteria for building a practical quantum computer, known as the DiVincenzo criteria
2001: IBM researchers implement Grover’s algorithm using NMR techniques and achieve a modest speedup over classical algorithms
في عام 2001 ، أظهر الباحثون خوارزمية Shor على العامل 15 باستخدام كمبيوتر NMR سعة 7 كيلو بايت.[37]
في عام 2005 ، بنى الباحثون في جامعة ميشيغان رقاقة أنصاف النواقل ion trap. مثل هذه الأجهزة من الطباعة الحجرية قد تشير إلى الطريق إلى الحوسبة الكمية القابلة للتطوير.[38]
2007: D-Wave Systems claims to have built the first commercial quantum computer, but its validity is disputed by many experts
في عام 2009 ، أنشأ الباحثون في جامعة ييل أول معالج الكم الحالة الصلبة. كان للرقاقة المزدوجة الموصلية - qubit ذرات اصطناعية ذرية مكونة من مليار ذرة ألومنيوم التي كانت بمثابة ذرة واحدة يمكن أن تشغل حالتين.[39][40]
قام فريق في جامعة بريستول أيضًا بإنشاء شريحة سيليكون تستند إلى البصريات الكمومية ، قادرة على تشغيل خوارزمية شور.[41]
حدثت تطورات أخرى في عام 2010.[42] يقوم Springer بنشر بمجلة ( معالجة معلومات الكم ) المخصصة لهذا الموضوع.[43]
في شباط (فبراير) 2010 ، تم تصميم الدارات الرقمية المختلطة مثل الجامع و الطارح وما إلى ذلك بمساعدة وظائف متناظرة منظمة من بوابات كمومية مختلفة..[44][45]
في أبريل 2011 ، حقق فريق من العلماء من أستراليا واليابان تقدماً مفاجئاً في النقل الكمي البعيد. لقد نجحوا في نقل مجموعة معقدة من البيانات الكمومية بسلامة نقلاً كاملاً ، دون التأثير على تراكبات الكيوبت.[46][47]

في عام 2011 ، أعلنت D-Wave Systems عن أول عملية تسخين و تبريد كمية تجارية ، D-Wave One ، ادّعت بامتلاكها معالج 128 كيلوبت. في 25 مايو 2011 ، من ثم وافق Lockheed Martin على شراء نظام D-Wave One.[48] ستضم شركة لوكهيد وجامعة جنوب كاليفورنيا (USC) جهاز D-Wave One في مركز الحوسبة الكمومية USC Lockheed Martin الذي تم تشكيله حديثًا.[49] صمم مهندسو D-Wave الرقائق بنهج تجريبي ، مع التركيز على حل مشكلات معينة. لقد أعجب المستثمرون بهذا أكثر من الأكاديميين الذين قالوا إن D-Wave لم يثبت أنهم يمتلكون بالفعل كمبيوترًا كمياً. تم تخفيف الانتقادات بعد نشر بحث في مجلة D-Wave في "[[[Nature (journal) | Nature]]" ، والتي أثبتت أن للرقائق بعض الخصائص الكمومية.[50][51] اقترحت ورقتان بحثيتان تم نشرهما أن تشغيل آلة D-Wave يمكن شرحها بشكل كلاسيكي ، بدلاً من طلب النماذج الكمومية.[52][53] أظهر العمل اللاحق أن النماذج الكلاسيكية غير كافية عند النظر في جميع البيانات المتاحة.[54] لا يزال الخبراء منقسمين حول التصنيف النهائي لأنظمة D-Wave على الرغم من أن سلوكهم الكمي تم تحديده بشكل ملموس مع عرض للتشابك.[55] خلال العام نفسه ، ابتكر الباحثون في جامعة بريستول نظامًا للبصريات بكامله يشغل نسخة من خوارزمية شور للعامل 21 بنجاح..[56]
في سبتمبر 2011 ، أثبت الباحثون أن أجهزة الكمبيوتر الكمومية يمكن تصنيعها باستخدام بنية Von Neumann (فصل ذاكرة الوصول العشوائي).[57]
في نوفمبر 2011 ، قام الباحثون بالتحليل إلى 143 عامل باستخدام 4 وحدات بت.[58]
في فبراير 2012 قال علماء IBM أنهم حققوا العديد من الاختراقات في مجال الحوسبة الكمومية باستخدام دارات متكاملة فائقة التوصيل.[59]
في أبريل 2012 ، قام فريق متعدد الجنسيات من الباحثين من جامعة جنوب كاليفورنيا ، جامعة دلفت للتكنولوجيا ، جامعة ولاية أيوا للعلوم والتكنولوجيا ، و جامعة كاليفورنيا ، سانتا بربارة ، ببناء كمبيوتر الكم اثنين qubit بإدخال الكريستال الماس التي يمكن بسهولة رفع مستوى الوظيفية في درجة حرارة الغرفة. تم استخدام اتجاهين منطقيين لqubit حيث يدور كل من الإلكترون ونواة النيتروجين ، مع نبضات الأمواج الميكروية . قام هذا الكمبيوتر بتشغيل خوارزمية Grover التي تولد الإجابة الصحيحة من المحاولة الأولى في 95٪ من الحالات.[60]
في سبتمبر 2012 ، قال باحثون أستراليون في جامعة نيو ساوث ويلز إن أول كمبيوتر كمومي في العالم كان على بعد 5 إلى 10 سنوات فقط ، بعد أن أعلن عن تقدم عالمي يتيح تصنيع كتل بناء الذاكرة الخاصة به. ابتكر فريق بحث بقيادة مهندسين أستراليين أول حقل عمل يعتمد على ذرة واحدة من السيليكون ، مستشهداً بنفس المنصة التكنولوجية التي تشكل الأساسيات لأجهزة الكمبيوتر الحديثة..[61][62]
في أكتوبر 2012 ، تم تقديم جائزة نوبل إلى David J. Wineland و Serge Haroche لعملهم الأساسي في فهم العالم الكوانتي ، مما قد يساعد في جعل الحوسبة الكمومية ممكنة.[63][64]
في نوفمبر 2012 ، أبلغ العلماء في جامعة العلوم والتكنولوجيا في الصين عن أول انتقال كمي من أداة ماكروسكوبية لأخرى في هيفي .[65][66]
في ديسمبر 2012 ، تأسست أول شركة برمجيات للحوسبة الكمومية ، 1QBit في فانكوفر ، كولومبيا البريطانية.[67] 1QBit هي أول شركة تركز حصريًا على تسويق تطبيقات البرامج لأجهزة الكمبيوتر الكمية المتاحة تجاريًا ، بما في ذلك D-Wave Two. أظهر بحث 1QBit قدرة فائقة التوصيل للكم الصلب على حل مشاكل العالم الحقيقي.[68]
في فبراير 2013 ، تم الإبلاغ عن تقنية جديدة ، أخذ عينات boson ، بواسطة مجموعتين تستخدمان فوتونات في شبكية بصرية ليست كمبيوترًا كموميًا عالميًا ولكنها قد تكون جيدة بما يكفي للمشاكل العملية. مجلة "العلوم" 15 فبراير 2013 في أيار (مايو) 2013 ، أعلنت Google عن إطلاقها لمختبر الكم للذكاء الاصطناعي ، الذي استضافته NASA 's مركز أبحاث Ames ، مع جهاز كمبيوتر الكم 512-Dbit. ستدعو USRA (رابطة أبحاث الفضاء في الجامعات) الباحثين إلى المشاركة في ذلك بهدف دراسة الحوسبة الكمومية للتعلم الآلي.[69] أضافت Google أنها "طورت بالفعل بعض خوارزميات تعلم الآلة الكمومية" و "تعلمت بعض المبادئ المفيدة" ، مثل أن "أفضل النتائج" تأتي من "خلط الكم والحوسبة الكلاسيكية".[69]
في أوائل عام 2014 ، تم الإبلاغ ، استنادًا إلى المستندات المقدمة من المقاول السابق لوكالة الأمن القومي إدوارد سنودن ، أن الولايات المتحدة وكالة الأمن القومي (NSA) تدير برنامجًا بحثيًا بقيمة 79.7 مليون دولار (بعنوان "اختراق الأهداف الصلبة") لتطوير جهاز كمبيوتر الكم قادر على كسر التشفير الضعيف .[70]
في عام 2014 ، أبلغت مجموعة من الباحثين من ETH Zürich و USC و Google و Microsoft عن تعريف للإسراع أو التعجيل الكمومي ، و لكن لم يتمكنوا من قياس تسريع الكم باستخدام جهاز D-Wave Two ، لكنه لم يستبعد صراحة.[71][72]
في عام 2014 ، استخدم الباحثون في جامعة نيو ساوث ويلز السيليكون كقشرة واقية حول qubit ، مما يجعلها أكثر دقة ، مما يزيد من طول الزمن الذي سوف يحتفظون فيه بالمعلومات ، وربما يجعل أجهزة الكمبيوتر الكمومية أسهل في البناء.[73]
في أبريل 2015 ، ادعى علماء IBM بتقدمين حاسمين نحو تحقيق كمبيوتر الكم العملي. لقد طالبوا بالقدرة على اكتشاف وقياس كلا النوعين من الأخطاء الكمومية في وقت واحد ، بالإضافة إلى تصميم جديد لدارة بت الكم المربع الذي يمكن أن يتوسع إلى أبعاد أكبر.[74]
في أكتوبر 2015 ، نجحت QuTech في اختبار عدم المساواة في Loophole-free Bell باستخدام دوران الإلكترون مفصول ب1.3 كيلومتر.[75]
في أكتوبر 2015 ، بنى الباحثون في جامعة نيو ساوث ويلز بوابة منطقية كمومية في السيليكون لأول مرة.[76] في ديسمبر 2015 ، عرضت ناسا علنًا أول كمبيوتر كمّي يعمل بكامل طاقته في العالم بقيمة 15 مليون دولار من صنع الشركة الكندية D-Wave في Quantum Artificial Intelligence Laboratory at its Ames Research Center ولاية كاليفورنيا موفيت فيلد. تم شراء الجهاز في عام 2013 عبر شراكة مع Google و Universities Space Research Association.يعتبر وجود واستخدام التأثيرات الكمومية في وحدة معالجة الكم D-Wave مقبولًا على نطاق واسع.[77] في بعض الاختبارات ، يمكن أن يُظهر أن المعالج الكمي للصلب D-Wave تفوقاً خوارزمية سيلبي.[78] تم تصنيع اثنين فقط من هذا الكمبيوتر حتى الآن.
في مايو 2016 ، أعلنت IBM Research [79] بأنه للمرة الأولى على الإطلاق ، بم إتاحة الحوسبة الكمومية لأفراد الجمهور سحابياً ، والذين يمكنهم الوصول إلى التجارب وتشغيلها على معالج الكم في IBM. تسمى الخدمة بـ IBM Quantum Experience. يتكون المعالج الكمومي من خمسة وحدات بت فائقة التوصيل ويوجد في IBM T. J. Watson Research Center في نيويورك. في أغسطس 2016 ، نجح العلماء في جامعة مريلاند في بناء أول كمبيوتر كمومي قابل للبرمجة.[80]
في أكتوبر 2016 ، وصفت جامعة بازل متغيرًا للكمبيوتر الكمومي القائم على الفتحة الإلكترونية، والذي بدلاً من التلاعب به بدوران الإلكترون تم استخدام ثقوب الإلكترون في أنصاف النواقل في درجات حرارة منخفضة (MK) والتي هي أقل عرضة للتآكل. تم تسمية هذا الكمبيوتر الكمومي "البوزيتروني" حيث يتصرف شبه الجسيمات كما لو كان له شحنة كهربائية موجبة.[81]
في مارس 2017 ، أعلنت شركة IBM عن مبادرة رائدة في هذا المجال لبناء أنظمة الحوسبة الكمومية المتاحة تجارياً والتي تسمى IBM Q. كما أصدرت الشركة واجهة برمجة تطبيقات جديدة (Application Program Interface) لـ IBM Quantum Experience التي تتيح للمطورون والمبرمجون للبدئ في بناء واجهات بين الكمبيوتر الكمومي القائم على الحوسبة السحابية (qubit) الحالية والحواسيب الكلاسيكية دون الحاجة إلى خلفية عميقة في فيزياء الكم.
في مايو 2017 ، أعلنت شركة IBM[82]أنها نجحت في بناء واختبار أقوى معالجات الحوسبة الكمومية العالمية. الأول هو معالج سعة 16 كيوبت والذي سيتيح إجراء تجارب أكثر تعقيدًا من معالج 5 كيوبت المتاح مسبقًا. والثاني هو أول معالج تجاري أولي من طراز IBM يحتوي على 17 كيوبت ويستفيد من تحسينات هامة في المواد والجهاز والهندسة المعمارية ليصبح أقوى معالج كمي الذي أنشأته شركة IBM حتى الآن. في يوليو 2017 ، أعلنت مجموعة من الباحثين الأمريكيين عن جهاز محاكاة الكم ب 51 بت. أعلن هذا ميخائيل لوكين من جامعة هارفارد في المؤتمر الدولي حول تقنيات الكم في موسكو.[83] جهاز محاكاة الكم يختلف عن جهاز الكمبيوتر. تم تصميم محاكاة Lukin لحل معادلة واحدة. حل معادلة مختلفة يتطلب بناء نظام جديد.و يمكن للكمبيوتر حل العديد من المعادلات المختلفة.
في سبتمبر 2017 ، استخدم علماء IBM Research جهازًا بحجم 7 كيوبت لتصميم أكبر جزيء,[84] البريليوم هيدريد ، من أي وقت مضى عن طريق جهاز كمبيوتر الكم. تم نشر النتائج كقصة غلاف في المجلة التي استعرضها النظراء Nature.
في أكتوبر 2017 ، نجح علماء أبحاث IBM في "كسر حاجز المحاكاة 49 كيوبت" و simulated 49- and 56-qubit short-depth circuits, باستخدام الحاسوب العملاق فولكان في مختبر لورانس ليفرمور الوطني ، وإطار الموتر أو الموجه العملاق لجامعة إلينوي (تم تطويره في الأصل في جامعة كاليفورنيا). ونشرت النتائج في arxiv.[85]
في نوفمبر 2017 ، نجح الفريق البحثي لجامعة سيدني في أستراليا في صنع circulator microwave ، وهو جزء هام من أجهزة الكمبيوتر الكمومية ، أصغر بمقدار 1000 مرة من الدارة التقليدية باستخدام العوازل الطوبوغرافية لإبطاء سرعة الضوء في المواد.[86]
في ديسمبر 2017 ، أعلنت شركة IBM[87]أول عملاء لشبكة IBM Q Network. تشمل الشركات والجامعات والمختبرات لاستكشاف التطبيقات الكمية العملية ، باستخدام أنظمة IBM Q 20 التجارية ، للأعمال التجارية والعلوم: JPMorgan Chase و Daimler AG و Samsung و JSR Corporation و Barclays و Hitachi Metals و Honda و Nagase و Keio University ، مختبر أوك ريدج الوطني ، جامعة أكسفورد وجامعة ملبورن. في ديسمبر 2017 ، أصدرت Microsoft نسخة معاينة من "مجموعة تطوير الكم".[88] يتضمن لغة برمجة ، Q # ، والتي يمكن استخدامها لكتابة البرامج التي يتم تشغيلها على جهاز كمبيوتر كمومي تمت محاكاته.
في عام 2017 ، أعلنت D-Wave بأنها بدأت في بيع جهاز كمبيوتر بحجم 2000 كيوبت.[89]
في أواخر عام 2017 وأوائل 2018 IBM,[90] Intel,[91] و غوغل[92] أعلنتا عن كل من معالجات كمومية للاختبار تحتوي على 50 و 49 و 72 كيوبت ، على التوالي ، كل ذلك باستخدام دوائر فائقة التوصيل. بعدد من البتات ، تقترب هذه الدوائر من النطاق الذي من المتوقع أن تصبح فيه محاكاة دينامياتها الكمومية باهظة على أجهزة الكمبيوتر الكلاسيكية ، على الرغم من أنه قيل إن هناك حاجة إلى مزيد من التحسينات في معدلات الخطأ لوضع المحاكاة الكلاسيكية بعيدة المنال.[93]
في فبراير 2018 ، أبلغ العلماء ، لأول مرة ، عن اكتشاف صيغة جديدة من الضوء ، والذي قد يشمل polariton ، والذي قد يكون مفيدًا في تطوير أجهزة الكمبيوتر الكمومية.[94][95]
في فبراير 2018 ، أبلغت شركة QuTech بنجاح عن اختبار معالج الكم القائم على السيليكون ثنائي النواة.[96] في يونيو 2018 ، بدأت شركة Intel في اختبار معالج الدوران المعتمد على السيليكون ، والذي تم تصنيعه في الشركة D1D Fab في ولاية أوريغون.[97]
في تموز (يوليو) 2018 ، حقق فريق بقيادة جامعة سيدني أول عرض متعدد الكيوبتات في العالم لحساب كيميائي الكم تم إجراؤه على نظام من الأيونات المحجوزة ، واحدة من منصات الأجهزة الرائدة في السباق لتطوير الكمبيوتر الكم العالمي.[98]
2019: Google announces that it has achieved quantum supremacy by performing a calculation on a 53-qubit quantum processor that would take a classical supercomputer thousands of years to complete
2020: IBM demonstrates that its 65-qubit quantum processor can perform calculations beyond the reach of any classical computer
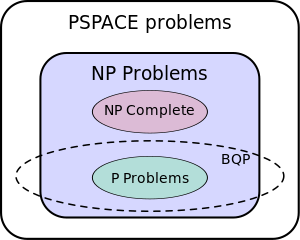
العلاقة بنظرية التعقد الحاسوبية
 مقالة مفصلة: نظرية التعقد الكمومية
مقالة مفصلة: نظرية التعقد الكمومية
التطبيقات المقترحة
إن أحد أكثر التطبيقات الواعدة للحواسيب الكمومية هو محاكاة سلوك المادة وصولاً إلى المستوى الجزيئي. فشركات تصنيع السيارات مثل فولكسڤاگن ودايملر تستخدم حواسيب كمومية لمحاكاة التركيب الكيميائي لبطاريات السيارات الكهربائية بهدف مساعدتها على إيجاد طرق جيدة لتحسين أدائها. وتقوم شركات مستحضرات الأدوية بإستخدام لتحليل ومقارنة المركبات التي يمكن أن تقودها إلى إنتاج عقارات جديدة.
كما وتعد هذه الآلات رائعة أيضاً بالنسبة لمسائل البحث عن الحلول الأمثلية، لأنها قادرة على معالجة عدد هائل من الحلول المحتملة بسرعات خارقة. فشركات إيرباص على سبيل المثال تستخدم هذه الآلات لتساعدها في حساب مسارات الصعود والهبوط الأكثر كفاءة في استهلاك الوقود بالنسبة للطائرات. وقد كشفت فولكسڤاگن الستار عن خدمة تقوم بحساب الطرق الأمثلية للحافلات وسيارات الأجرة ضمن المدن لتخفيض الازدحام إلى الحد الأدنى، كما أن بعض الباحثين يعتقدون أيضاً أنه يمكن إستخدام الآلات الكمومية في تسريع الذكاء الاصطناعي.
قد يستغرق الأمر بضع سنوات قبل أن تتمكن الحواسيب الكمومية من بلوغ أقصى إمكانياتها، حيث تواجه الجامعات والشركات التي تعمل على تطويرها نقصاً في عدد الباحثين من أصحاب المهارات العالية في هذا المجال، ونقصاً في عدد الموردين لبعض المكونات الأساسية. ولكن إذا تمكنت هذه الآلات الحاسوبية الجديدة الغريبة من الإيفاء بوعودها، فقد تتمكن من تحويل صناعات بأكملها، وتعزيز الإبتكار العالمي بشكل كبير.
انظر أيضاً
- الحاسوب الكمومي قاب قوسين أو أدنى
- الحوسبة الفوتونية Photonic computing
- خط زمني للحوسبة الكمومية Timeline of quantum computing
- حافلة كمومية
- علم التعمية بعد الكمومية Post-quantum cryptography
- الحاسوب الكيميائي Chemical computer
- حاسوب الدنا DNA computer
- الحاسوب الجزيئي Molecular computer
- قائمة التقنيات الناشئة List of emerging technologies
- خوارزميات كمومية
- خوارزمية شور Shor
- خوارزمية گروڤر Grover
- خوارزمية سايمون Simon
الهامش
- ^ "IBM Quantum Update: Q System One Launch, New Collaborators, and QC Center Plans". HPCwire. 10 January 2019.
- ^ Chan, Rosalie. "IBM unveils the world's first quantum computer that businesses can actually use to solve previously impossible problems". Business Insider.
- ^ Coleman, Lauren deLisa. "CES 2019: Why IBM CEO Ginni Rometty's Opening Address Delivers". Forbes.
- ^ Waldner, Jean-Baptiste (2007). Nanocomputers and Swarm Intelligence. London: ISTE. p. 157. ISBN 2746215160.
- ^ DiVincenzo, David P. (1995). "Quantum Computation". Science. 270 (5234): 255–261. Bibcode:1995Sci...270..255D. CiteSeerX 10.1.1.242.2165. doi:10.1126/science.270.5234.255. (يتطلب اشتراك)
- ^ "دليلك الشامل- ما هو الحاسوب الكمومي؟". إم آي تي تكنولوجي رڤيو. 2019-02-08. Retrieved 2019-02-08.
- ^ Lenstra, Arjen K. (2000). "Integer Factoring" (PDF). Designs, Codes and Cryptography. 19 (2/3): 101–128. doi:10.1023/A:1008397921377. Archived from the original (PDF) on 2015-04-10.
{{cite journal}}: Unknown parameter|deadurl=ignored (|url-status=suggested) (help) - ^ Quantum Algorithm Zoo – Stephen Jordan's Homepage
- ^ Jon Schiller, Phd (2009-06-19). Quantum Computers. ISBN 9781439243497.
- ^ Norton, Quinn (2007-02-15). "The Father of Quantum Computing". Wired.
- ^ Ambainis, Andris (Spring 2014). "What Can We Do with a Quantum Computer?". Institute for Advanced Study.
- ^ Ambainis, Andris; Hassidim, Avinatan; Lloyd, Seth (2008). "Quantum algorithm for solving linear systems of equations". Physical Review Letters. 103 (15): 150502. arXiv:0811.3171. doi:10.1103/PhysRevLett.103.150502. PMID 19905613.
- ^ DiVincenzo, David P. (2000-04-13). "The Physical Implementation of Quantum Computation". Fortschritte der Physik. 48 (9–11): 771–783. arXiv:quant-ph/0002077. Bibcode:2000ForPh..48..771D. doi:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E.
- ^ Das, A.; Chakrabarti, B. K. (2008). "Quantum Annealing and Analog Quantum Computation". Rev. Mod. Phys. 80 (3): 1061–1081. arXiv:0801.2193. Bibcode:2008RvMP...80.1061D. CiteSeerX 10.1.1.563.9990. doi:10.1103/RevModPhys.80.1061.
- ^ Nayak, Chetan; Simon, Steven; Stern, Ady; Das Sarma, Sankar (2008). "Nonabelian Anyons and Quantum Computation". Rev Mod Phys. 80 (3): 1083–1159. arXiv:0707.1889. Bibcode:2008RvMP...80.1083N. doi:10.1103/RevModPhys.80.1083.
- ^ Clarke, John; Wilhelm, Frank (June 19, 2008). "Superconducting quantum bits". Nature. 453 (7198): 1031–1042. Bibcode:2008Natur.453.1031C. doi:10.1038/nature07128. PMID 18563154.
- ^ Kaminsky, William M (2004). "Scalable Superconducting Architecture for Adiabatic Quantum Computation". arXiv:quant-ph/0403090.
- ^ Imamoğlu, Atac; Awschalom, D. D.; Burkard, Guido; DiVincenzo, D. P.; Loss, D.; Sherwin, M.; Small, A. (1999). "Quantum information processing using quantum dot spins and cavity-QED". Physical Review Letters. 83 (20): 4204–4207. arXiv:quant-ph/9904096. Bibcode:1999PhRvL..83.4204I. doi:10.1103/PhysRevLett.83.4204.
- ^ Fedichkin, Leonid; Yanchenko, Maxim; Valiev, Kamil (2000). "Novel coherent quantum bit using spatial quantization levels in semiconductor quantum dot". Quantum Computers and Computing. 1: 58–76. arXiv:quant-ph/0006097. Bibcode:2000quant.ph..6097F. Archived from the original on 2011-08-18.
{{cite journal}}: Unknown parameter|deadurl=ignored (|url-status=suggested) (help) - ^ Bertoni, A.; Bordone, P.; Brunetti, R.; Jacoboni, C.; Reggiani, S. (2000-06-19). "Quantum Logic Gates based on Coherent Electron Transport in Quantum Wires". Physical Review Letters. 84 (25): 5912–5915. Bibcode:2000PhRvL..84.5912B. doi:10.1103/PhysRevLett.84.5912. PMID 10991086.
- ^ Ionicioiu, Radu; Amaratunga, Gehan; Udrea, Florin (2001-01-20). "Quantum Computation with Ballistic Electrons". International Journal of Modern Physics B (in الإنجليزية). 15 (2): 125–133. arXiv:quant-ph/0011051. Bibcode:2001IJMPB..15..125I. doi:10.1142/s0217979201003521. ISSN 0217-9792.
- ^ Ramamoorthy, A.; Bird, J. P.; Reno, J. L. (2007). "Using split-gate structures to explore the implementation of a coupled-electron-waveguide qubit scheme". Journal of Physics: Condensed Matter (in الإنجليزية). 19 (27): 276205. Bibcode:2007JPCM...19A6205R. doi:10.1088/0953-8984/19/27/276205. ISSN 0953-8984.
- ^ Leuenberger, MN; Loss, D (Apr 12, 2001). "Quantum computing in molecular magnets". Nature. 410 (6830): 789–93. arXiv:cond-mat/0011415. Bibcode:2001Natur.410..789L. doi:10.1038/35071024. PMID 11298441.
- ^ Knill, G. J.; Laflamme, R.; Milburn, G. J. (2001). "A scheme for efficient quantum computation with linear optics". Nature. 409 (6816): 46–52. Bibcode:2001Natur.409...46K. doi:10.1038/35051009. PMID 11343107.
- ^ Nizovtsev, A. P. (August 2005). "A quantum computer based on NV centers in diamond: Optically detected nutations of single electron and nuclear spins". Optics and Spectroscopy. 99 (2): 248–260. Bibcode:2005OptSp..99..233N. doi:10.1134/1.2034610.
- ^ Gruener, Wolfgang (2007-06-01). "Research indicates diamonds could be key to quantum storage". Archived from the original on 2007-06-04. Retrieved 2007-06-04.
{{cite web}}: Unknown parameter|deadurl=ignored (|url-status=suggested) (help) - ^ Neumann, P.; et al. (June 6, 2008). "Multipartite Entanglement Among Single Spins in Diamond". Science. 320 (5881): 1326–1329. Bibcode:2008Sci...320.1326N. doi:10.1126/science.1157233. PMID 18535240.
- ^ Millman, Rene (2007-08-03). "Trapped atoms could advance quantum computing". ITPro. Archived from the original on 2007-09-27. Retrieved 2007-07-26.
- ^ Ohlsson, N.; Mohan, R. K.; Kröll, S. (January 1, 2002). "Quantum computer hardware based on rare-earth-ion-doped inorganic crystals". Opt. Commun. 201 (1–3): 71–77. Bibcode:2002OptCo.201...71O. doi:10.1016/S0030-4018(01)01666-2.
- ^ Longdell, J. J.; Sellars, M. J.; Manson, N. B. (September 23, 2004). "Demonstration of conditional quantum phase shift between ions in a solid". Phys. Rev. Lett. 93 (13): 130503. arXiv:quant-ph/0404083. Bibcode:2004PhRvL..93m0503L. doi:10.1103/PhysRevLett.93.130503. PMID 15524694.
- ^ Náfrádi, Bálint; Choucair, Mohammad; Dinse, Klaus-Peter; Forró, László (July 18, 2016). "Room Temperature manipulation of long lifetime spins in metallic-like carbon nanospheres". Nature Communications. 7: 12232. arXiv:1611.07690. Bibcode:2016NatCo...712232N. doi:10.1038/ncomms12232. PMC 4960311. PMID 27426851.
- ^ Benioff, Paul (1980). "The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines". Journal of Statistical Physics. 22 (5): 563–591. Bibcode:1980JSP....22..563B. doi:10.1007/bf01011339.
- ^ Manin, Yu I (1980). "Vychislimoe i nevychislimoe" [Computable and Noncomputable]. Sov.Radio (in الروسية). pp. 13–15. Archived from the original on May 10, 2013. Retrieved October 20, 2017.
- ^ Gil, Dario (May 4, 2016). "The Dawn of Quantum Computing is Upon Us". Retrieved May 4, 2016.
- ^ Bennett,, C. H. (29 March 1993). "Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels" (PDF). Physical Review Letters. 70 (13): 1895–1899. Bibcode:1993PhRvL..70.1895B. doi:10.1103/PhysRevLett.70.1895. PMID 10053414.
{{cite journal}}: CS1 maint: extra punctuation (link) - ^ Ekert, Artur; Josza, Richard (1996). "Quantum computation and Shor's factoring algorithm". Rev. Mod. Phys. 68 (3): 733–753. doi:10.1103/RevModPhys.68.733.
- ^ Vandersypen, Lieven M. K.; Steffen, Matthias; Breyta, Gregory; Yannoni, Costantino S.; Sherwood, Mark H.; Chuang, Isaac L. (2001). "Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance". Nature. 414 (6866): 883–7. arXiv:quant-ph/0112176. Bibcode:2001Natur.414..883V. CiteSeerX 10.1.1.251.8799. doi:10.1038/414883a. PMID 11780055.
- ^ "U-M develops scalable and mass-producible quantum computer chip". University of Michigan. 2005-12-12. Retrieved 2006-11-17.
- ^ DiCarlo, L.; Chow, J. M.; Gambetta, J. M.; Bishop, Lev S.; Johnson, B. R.; Schuster, D. I.; Majer, J.; Blais, A.; Frunzio, L.; S. M. Girvin; R. J. Schoelkopf (9 July 2009). "Demonstration of two-qubit algorithms with a superconducting quantum processor" (PDF). Nature. 460 (7252): 240–4. arXiv:0903.2030. Bibcode:2009Natur.460..240D. doi:10.1038/nature08121. PMID 19561592. Retrieved 2009-07-02.
- ^ "Scientists Create First Electronic Quantum Processor". Yale University. 2009-07-02. Archived from the original on 2010-06-11. Retrieved 2009-07-02.
{{cite web}}: Unknown parameter|deadurl=ignored (|url-status=suggested) (help) - ^ "Code-breaking quantum algorithm runs on a silicon chip". New Scientist. 2009-09-04. Retrieved 2009-10-14.
- ^ "New Trends in Quantum Computation". Simons Conference on New Trends in Quantum Computation 2010: Program. C.N. Yang Institute for Theoretical Physics.
- ^ "Quantum Information Processing". Springer.com. Retrieved on 2011-05-19.
- ^ Bhattacharjee, Pijush Kanti (2010). "Digital Combinational Circuits Design by QCA Gates" (PDF). International Journal of Computer and Electrical Engineering. 2 (1): 67–72.
- ^ Bhattacharjee, Pijush Kanti (2010). "Digital Combinational Circuits Design with the Help of Symmetric Functions Considering Heat Dissipation by Each QCA Gate" (PDF). International Journal of Computer and Electrical Engineering. 2 (4): 666–672.
- ^ "Quantum teleporter breakthrough". University of New South Wales. 2011-04-15. Archived from the original on 2011-04-18.
- ^ Lai, Richard (2011-04-18). "First light wave quantum teleportation achieved, opens door to ultra fast data transmission". Engadget.
- ^ "D-Wave Systems sells its first Quantum Computing System to Lockheed Martin Corporation". D-Wave. 2011-05-25. Retrieved 2011-05-30.
- ^ "Operational Quantum Computing Center Established at USC". University of Southern California. 2011-10-29. Retrieved 2011-12-06.
- ^ Johnson, M. W.; Amin, M. H. S.; Gildert, S.; Lanting, T.; Hamze, F.; Dickson, N.; Harris, R.; Berkley, A. J.; Johansson, J.; Bunyk, P.; Chapple, E. M.; Enderud, C.; Hilton, J. P.; Karimi, K.; Ladizinsky, E.; Ladizinsky, N.; Oh, T.; Perminov, I.; Rich, C.; Thom, M. C.; Tolkacheva, E.; Truncik, C. J. S.; Uchaikin, S.; Wang, J.; Wilson, B.; Rose, G. (12 May 2011). "Quantum annealing with manufactured spins". Nature. 473 (7346): 194–198. Bibcode:2011Natur.473..194J. doi:10.1038/nature10012. PMID 21562559.
- ^ Simonite, Tom (October 4, 2012). "The CIA and Jeff Bezos Bet on Quantum Computing". Technology Review.
- ^ Seung Woo Shin; Smith, Graeme; Smolin, John A.; Vazirani, Umesh (2014-05-02). "How "Quantum" is the D-Wave Machine?". arXiv:1401.7087 [quant-ph].
- ^ Boixo, Sergio; Rønnow, Troels F.; Isakov, Sergei V.; Wang, Zhihui; Wecker, David; Lidar, Daniel A.; Martinis, John M.; Troyer, Matthias (2014). "Quantum Annealing With More Than 100 Qbits". Nature Physics. 10 (3): 218–224. arXiv:1304.4595. Bibcode:2014NatPh..10..218B. doi:10.1038/nphys2900.
- ^ Albash, Tameem; Rønnow, Troels F.; Troyer, Matthias; Lidar, Daniel A. (2014-09-12). "Reexamining classical and quantum models for the D-Wave One processor". The European Physical Journal Special Topics. 224 (111): 111–129. arXiv:1409.3827. Bibcode:2015EPJST.224..111A. doi:10.1140/epjst/e2015-02346-0.
- ^ Lanting, T.; Przybysz, A. J.; Smirnov, A. Yu.; Spedalieri, F. M.; Amin, M. H.; Berkley, A. J.; Harris, R.; Altomare, F.; Boixo, S.; Bunyk, P.; Dickson, N.; Enderud, C.; Hilton, J. P.; Hoskinson, E.; Johnson, M. W.; Ladizinsky, E.; Ladizinsky, N.; Neufeld, R.; Oh, T.; Perminov, I.; Rich, C.; Thom, M. C.; Tolkacheva, E.; Uchaikin, S.; Wilson, A. B.; Rose, G. (2014-05-29). "Entanglement in a quantum annealing processor". Physical Review X. 4 (2): 021041. arXiv:1401.3500. Bibcode:2014PhRvX...4b1041L. doi:10.1103/PhysRevX.4.021041.
- ^ Lopez, Enrique Martin; Laing, Anthony; Lawson, Thomas; Alvarez, Roberto; Zhou, Xiao-Qi; O'Brien, Jeremy L. (2012). "Implementation of an iterative quantum order finding algorithm". Nature Photonics. 6 (11): 773–776. arXiv:1111.4147. Bibcode:2012NaPho...6..773M. doi:10.1038/nphoton.2012.259.
- ^ Mariantoni, Matteo; Wang, H.; Yamamoto, T.; Neeley, M.; Bialczak, Radoslaw C.; Chen, Y.; Lenander, M.; Lucero, Erik; O'Connell, A. D.; Sank, D.; Weides, M.; Wenner, J.; Yin, Y.; Zhao, J.; Korotkov, A. N.; Cleland, A. N.; Martinis, John M. (2011). "Quantum computer with Von Neumann architecture". Science. 334 (6052): 61–65. arXiv:1109.3743. Bibcode:2011Sci...334...61M. doi:10.1126/science.1208517. PMID 21885732.
- ^ Xu, Nanyang; Zhu, Jing; Lu, Dawei; Zhou, Xianyi; Peng, Xinhua; Du, Jiangfeng (2011). "Quantum Factorization of 143 on a Dipolar-Coupling NMR system". Physical Review Letters. 109 (26): 269902. arXiv:1111.3726. Bibcode:2012PhRvL.109z9902X. doi:10.1103/PhysRevLett.109.269902.
- ^ "IBM Says It's 'On the Cusp' of Building a Quantum Computer". PCMAG. Retrieved 2014-10-26.
- ^ "Quantum computer built inside diamond". Futurity. 2012-04-09. Retrieved 2014-10-26.
- ^ "Australian engineers write quantum computer 'qubit' in global breakthrough". The Australian. Retrieved 2012-10-03.
- ^ "Breakthrough in bid to create first quantum computer". University of New South Wales. 2012-09-19. Retrieved 2012-10-03.
- ^ Frank, Adam (October 14, 2012). "Cracking the Quantum Safe". The New York Times. Retrieved 2012-10-14.
- ^ Overbye, Dennis (October 9, 2012). "A Nobel for Teasing Out the Secret Life of Atoms". The New York Times. Retrieved 2012-10-14.
- ^ "First Teleportation from One Macroscopic Object to Another: The Physics arXiv Blog". MIT Technology Review. November 15, 2012. Retrieved 2012-11-17.
{{cite web}}: Cite has empty unknown parameter:|booktitle=(help) - ^ Bao, Xiao-Hui; Xu, Xiao-Fan; Li, Che-Ming; Yuan, Zhen-Sheng; Lu, Chao-Yang; Pan, Jian-wei (November 13, 2012). "Quantum teleportation between remote atomic-ensemble quantum memories". Proceedings of the National Academy of Sciences. 109 (50): 20347–20351. arXiv:1211.2892. Bibcode:2012PNAS..10920347B. doi:10.1073/pnas.1207329109. PMC 3528515. PMID 23144222.
- ^ "1QBit Founded". 1QBit.com. Retrieved 2014-06-22.
- ^ "1QBit Research". 1QBit.com. Retrieved 2014-06-22.
- ^ أ ب "Launching the Quantum Artificial Intelligence Lab". Research@Google Blog. Retrieved 2013-05-16.
We've already developed some quantum machine learning algorithms. One produces very compact, efficient recognizers -- very useful when you're short on power, as on a mobile device. Another can handle highly polluted training data, where a high percentage of the examples are mislabeled, as they often are in the real world. And we've learned some useful principles: e.g., you get the best results not with pure quantum computing, but by mixing quantum and classical computing.
- ^ "NSA seeks to build quantum computer that could crack most types of encryption". Washington Post. January 2, 2014.
- ^ Ambainis, Andris; Wang, Z.; Job, J.; Boixo, S.; Isakov, S. V.; Wecker, D.; Martinis, J. M.; Lidar, D. A.; Troyer, M. (2014). "Defining and detecting quantum speedup". Science. 345 (6195): 420–424. arXiv:1401.2910v1. doi:10.1126/science.1252319. PMID 25061205.
- ^ "Quantum Chaos: After a Failed Speed Test, the D-Wave Debate Continues". Scientific American. 2014-06-19.
- ^ Gaudin, Sharon (23 October 2014). "Researchers use silicon to push quantum computing toward reality". Computer World.
- ^ "IBM achieves critical steps to first quantum computer". www-03.ibm.com. 29 April 2015.
- ^ Hensen, B. "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres". Nature.
- ^ Condliffe, Jamie. "World's First Silicon Quantum Logic Gate Brings Quantum Computing One Step Closer".
- ^ "3Q: Scott Aaronson on Google's new quantum-computing paper". MIT News. Retrieved 2016-01-05.
- ^ قالب:Cite arxiv
- ^ "IBM Makes Quantum Computing Available on IBM Cloud to Accelerate Innovation". May 4, 2016. Retrieved May 4, 2016.
- ^ MacDonald, Fiona. "Researchers have built the first reprogrammable quantum computer". ScienceAlert. Retrieved 8 August 2016.
- ^ "A new Type of Quantum Bit". www.unibas.ch.
- ^ "IBM Builds Its Most Powerful Universal Quantum Computing Processors". 17 May 2017. Retrieved 17 May 2017.
- ^ Reynolds, Matt. "Quantum simulator with 51 qubits is largest ever". New Scientist. Retrieved 23 July 2017.
- ^ "IBM Pioneers New Approach to Simulate Chemistry with Quantum Computing". 13 September 2017. Retrieved 13 September 2017.
- ^ قالب:Cite arxiv
- ^ "Key component for quantum computing invented: University of Sydney team develop microcircuit based on Nobel Prize research".
- ^ "IBM Announces Collaboration with Leading Fortune 500 Companies, Academic Institutions and National Research Labs to Accelerate Quantum Computing". 14 November 2017. Retrieved 14 December 2017.
- ^ Microsoft Mechanics (11 December 2017). "Microsoft Quantum Development Kit: Introduction and step-by-step demo" – via YouTube.
- ^ Temperton, James (26 January 2017). "Got a spare $15 million? Why not buy your very own D-Wave quantum computer". Wired. Retrieved 13 May 2018.
- ^ Will Knight (2017-11-10). "IBM Raises the Bar with a 50-Qubit Quantum Computer". MIT Technology Review. Retrieved 2017-12-13.
- ^ Hsu, Jeremy (January 9, 2018). "CES 2018: Intel's 49-Qubit Chip Shoots for Quantum Supremacy". Institute of Electrical and Electronics Engineers. Retrieved July 5, 2018.
- ^ Susan Curtis (2018-03-06). "Google aims for quantum supremacy". PhysicsWorld (in الإنجليزية الأمريكية). Retrieved 2018-09-12.
- ^ Tom Simonite (2018-05-19). "Google, Alibaba Spar Over Timeline for "Quantum Supremacy"". Wired. Retrieved 2018-09-12.
- ^ Hignett, Katherine (16 February 2018). "Physics Creates New Form Of Light That Could Drive The Quantum Computing Revolution". Newsweek. Retrieved 17 February 2018.
- ^ Liang, Qi-Yu; et al. (16 February 2018). "Observation of three-photon bound states in a quantum nonlinear medium". Science. 359 (6377): 783–786. arXiv:1709.01478. Bibcode:2018Sci...359..783L. doi:10.1126/science.aao7293. PMID 29449489. Retrieved 17 February 2018.
- ^ Giles, Martin (February 15, 2018). "Old-fashioned silicon might be the key to building ubiquitous quantum computers". MIT Technology Review. Retrieved July 5, 2018.
- ^ Forrest, Conner (June 12, 2018). "Why Intel's smallest spin qubit chip could be a turning point in quantum computing". TechRepublic. Retrieved July 12, 2018.
- ^ "World-first quantum computer simulation of chemical bonds using trapped ions: Quantum chemistry expected to be one of the first applications of full-scale quantum computers". ScienceDaily (in الإنجليزية). Retrieved 2018-08-13.
- ^ Michael Nielsen and Isaac Chuang (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. ISBN 0-521-63503-9. OCLC 174527496.
روابط خارجية
- موقع المعهد القومي الأمريكي للمعايير والتقانة الخاص بأبحاث الحواسيب الكمومية
- كوانتيكي بوابة وويكي خاصة بالحواسيب الكمومية
- TOQC: كتاب مجاني يستعرض مبادئ الحواسيب الكمومية.
- Stanford Encyclopedia of Philosophy: "Quantum Computing" by Amit Hagar.
- Quantiki - Wiki and portal with free-content related to quantum information science.
- jQuantum: Java quantum circuit simulator
- QCAD: Quantum circuit emulator
- C++ Quantum Library
- Haskell Library for Quantum computations
- Video Lectures by David Deutsch
- Lectures at the Institut Henri Poincaré (slides and videos)
- Online lecture on An Introduction to Quantum Computing, Edward Gerjuoy (2008)
- Online Web-based Quantum Computer Simulator (University Of Patras, Wire Communications Laboratory)
- مدونة سكوت آندرسون: أحد باحثي معهد MIT الرائدين في مجال الحواسيب الكمومية.
- صفحات تحتوي روابط لمحتوى للمشتركين فقط
- CS1 errors: unsupported parameter
- CS1 الروسية-language sources (ru)
- CS1 الإنجليزية الأمريكية-language sources (en-us)
- Articles with hatnote templates targeting a nonexistent page
- علم المعلومات الكمومية
- نماذج حاسوبية
- علم التعمية الكمومية
- نظرية المعلومات
- نظرية التعقد الحاسوبية
- رتب الحواسب
- علم الحاسب النظري