معامل يَنگ

معامل ينج/يونغ Young's modulus هو خاصية ميكانيكية للمواد الصلبة تقيس the tensile or compressive stiffness when the force is applied lengthwise. وهو معامل المرونة (Elastic Modulus or Modulus of Elasticity) يسمى أيضا معامل يونگ (Young's Modulus) هو ميل الجزء الأولى المستقيم في منحنى الإجهاد و الانفعال. ويقتصر على المواد الصلبة فقط و هو نسبة الاجهاد إلى الانفعال، وحدة معامل يونج (ي) هي: نيوتن /م2
معامل يونگ سـُمي على اسم توماس يونگ، العالم البريطاني من القرن الثامن عشر. إلا أن المفهوم كان قد طوره في 1727 ليونهارد اويلر، وأول التجارب التي استخدمت مفهوم معامل يونگ بصيغته الحالية أجراها العالم الإيطالي جوردانو ريكاتي في 1782 - قبل أبحاث يونگ بخمس وعشرون سنة.[1]
Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The first experiments that used the concept of Young's modulus in its modern form were performed by the Italian scientist Giordano Riccati in 1782, pre-dating Young's work by 25 years.[2] The term modulus is derived from the Latin root term modus, which means measure.
التعريف
معامل ينگ، ، يحدد كمِّياً العلاقة بين الإجهاد الشدي والانضغاطي (force per unit area) والانفعال المحوري (proportional deformation) في منطقة المرونة الخطية للمادة:[3]
Young's modulus is commonly measured in the International System of Units (SI) in multiples of the pascal (Pa) and common values are in the range of gigapascals (GPa).
أمثلة:
- Rubber (increasing pressure: length increases quickly, meaning low )
- Aluminium (increasing pressure: length increases slowly, meaning high )
المرونة الخطية
A solid material undergoes elastic deformation when a small load is applied to it in compression or extension. Elastic deformation is reversible, meaning that the material returns to its original shape after the load is removed.
At near-zero stress and strain, the stress–strain curve is linear, and the relationship between stress and strain is described by Hooke's law that states stress is proportional to strain. The coefficient of proportionality is Young's modulus. The higher the modulus, the more stress is needed to create the same amount of strain; an idealized rigid body would have an infinite Young's modulus. Conversely, a very soft material (such as a fluid) would deform without force, and would have zero Young's modulus.
خصائص متعلقة ولكن متميزة
Material stiffness is a distinct property from the following:
- Strength: maximum amount of stress that material can withstand while staying in the elastic (reversible) deformation regime;
- Geometric stiffness: a global characteristic of the body that depends on its shape, and not only on the local properties of the material; for instance, an I-beam has a higher bending stiffness than a rod of the same material for a given mass per length;
- Hardness: relative resistance of the material's surface to penetration by a harder body;
- Toughness: amount of energy that a material can absorb before fracture.
الاستخدام
Young's modulus enables the calculation of the change in the dimension of a bar made of an isotropic elastic material under tensile or compressive loads. For instance, it predicts how much a material sample extends under tension or shortens under compression. The Young's modulus directly applies to cases of uniaxial stress; that is, tensile or compressive stress in one direction and no stress in the other directions. Young's modulus is also used in order to predict the deflection that will occur in a statically determinate beam when a load is applied at a point in between the beam's supports.
Other elastic calculations usually require the use of one additional elastic property, such as the shear modulus , bulk modulus , and Poisson's ratio . Any two of these parameters are sufficient to fully describe elasticity in an isotropic material. For example, calculating physical properties of cancerous skin tissue, has been measured and found to be a Poisson’s ratio of 0.43±0.12 and an average Young’s modulus of 52 KPa. Defining the elastic properties of skin may become the first step in turning elasticity into a clinical tool.[4] For homogeneous isotropic materials simple relations exist between elastic constants that allow calculating them all as long as two are known:
الخطي مقابل اللاخطي
Young's modulus represents the factor of proportionality in Hooke's law, which relates the stress and the strain. However, Hooke's law is only valid under the assumption of an elastic and linear response. Any real material will eventually fail and break when stretched over a very large distance or with a very large force; however, all solid materials exhibit nearly Hookean behavior for small enough strains or stresses. If the range over which Hooke's law is valid is large enough compared to the typical stress that one expects to apply to the material, the material is said to be linear. Otherwise (if the typical stress one would apply is outside the linear range), the material is said to be non-linear.
Steel, carbon fiber and glass among others are usually considered linear materials, while other materials such as rubber and soils are non-linear. However, this is not an absolute classification: if very small stresses or strains are applied to a non-linear material, the response will be linear, but if very high stress or strain is applied to a linear material, the linear theory will not be enough. For example, as the linear theory implies reversibility, it would be absurd to use the linear theory to describe the failure of a steel bridge under a high load; although steel is a linear material for most applications, it is not in such a case of catastrophic failure.
In solid mechanics, the slope of the stress–strain curve at any point is called the tangent modulus. It can be experimentally determined from the slope of a stress–strain curve created during tensile tests conducted on a sample of the material.
المواد الاتجاهية
Young's modulus is not always the same in all orientations of a material. Most metals and ceramics, along with many other materials, are isotropic, and their mechanical properties are the same in all orientations. However, metals and ceramics can be treated with certain impurities, and metals can be mechanically worked to make their grain structures directional. These materials then become anisotropic, and Young's modulus will change depending on the direction of the force vector.[5] Anisotropy can be seen in many composites as well. For example, carbon fiber has a much higher Young's modulus (is much stiffer) when force is loaded parallel to the fibers (along the grain). Other such materials include wood and reinforced concrete. Engineers can use this directional phenomenon to their advantage in creating structures.
الاعتماد على درجة الحرارة
The Young's modulus of metals varies with the temperature and can be realized through the change in the interatomic bonding of the atoms, and hence its change is found to be dependent on the change in the work function of the metal. Although classically, this change is predicted through fitting and without a clear underlying mechanism (for example, the Watchman's formula), the Rahemi-Li model[6] demonstrates how the change in the electron work function leads to change in the Young's modulus of metals and predicts this variation with calculable parameters, using the generalization of the Lennard-Jones potential to solids. In general, as the temperature increases, the Young's modulus decreases via where the electron work function varies with the temperature as and is a calculable material property which is dependent on the crystal structure (for example, BCC, FCC). is the electron work function at T=0 and is constant throughout the change.
الحساب
معامل يونگ, E, يمكن حسابه بقسمة جهد الشد على انفعال الشد:
حيث
- E is the معامل يونگ (معامل المرونة) measured in pascals;
- F is the force applied to the object;
- A0 is the original cross-sectional area through which the force is applied;
- ΔL is the amount by which the length of the object changes;
- L0 is the original length of the object.
القوة المبذولة بمادة مشدودة أو مضغوطة
معامل يونگ لمادة can be used to calculate the force it exerts under a specific strain.
where F is the force exerted by the material when compressed or stretched by ΔL.
From this formula can be derived Hooke's law, which describes the stiffness of an ideal spring:
where
طاقة الجهد المرن
The elastic potential energy stored is given by the integral of this expression with respect to L:
where Ue is the elastic potential energy.
The elastic potential energy per unit volume is given by:
- , where is the strain in the material.
This formula can also be expressed as the integral of Hooke's law:
القيم التقريبية
معامل يونگ قد تغير قيمته بسبب اختلاف تركيب العينة وطريقة الاختبار. القيم المعطاة هنا هي تقريبية.
| المادة | معامل يونگ (E) in GPa | معامل يونگ (E) in lbf/in² (psi) |
|---|---|---|
| مطاط (small strain) | 0.01-0.1 | 1,500-15,000 |
| PTFE (تفلون) | 0.5 | 75000 |
| Low density polyethylene | 0.2 | 30,000 |
| HDPE | 1.379 | 200000 |
| Polypropylene | 1.5-2 | 217,000-290,000 |
| Bacteriophage capsids | 1-3 | 150,000-435,000 |
| Polyethylene terephthalate | 2-2.5 | 290,000-360,000 |
| Polystyrene | 3-3.5 | 435,000-505,000 |
| نايلون | 3-7 | 290,000-580,000 |
| Oak خشب (along grain) | 11 | 1,600,000 |
| Pine خشب (along grain) | 8.963 | 1,300,000 |
| MDF (wood composite) | 3.654 | 530,000 |
| خرسانة عالية القوة (تحت الضغط) | 30 | 4,350,000 |
| مغنسيوم معدن (Mg) | 45 | 6,500,000 |
| سبيكة ألومنيوم | 69 | 10,000,000 |
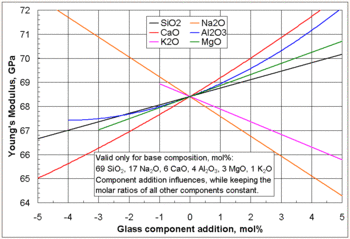
| زجاج (see also diagram below table) | 65-90 | 9,400,000-13,000,000 |
| Brass وبرونز | 103-124 | 17,000,000 |
| تيتانيوم (Ti) | 105-120 | 15,000,000-17,500,000 |
| نحاس (Cu) | 110-130 | 16,000,000-19,000,000 |
| بلاستيك مقوي بألياف الكربون (50/50 fibre/matrix, unidirectional, along grain) | 125-150 | 18,000,000 - 22,000,000 |
| حديد مطاوع وصلب | 190-210 | 30,000,000 |
| بريليوم (Be) | 287 | 41,500,000 |
| تنگستن (W) | 400-410 | 58,000,000-59,500,000 |
| كربيد السليكون (SiC) | 450 | 65,000,000 |
| اوزميوم (Os)[7] | 550 | |
| كربيد التنگستن (WC) | 450-650 | 65,000,000-94,000,000 |
| Single carbon nanotube [1] | 1,000+ | 145,000,000+ |
| ألماس (C) | 1,050-1,200 | 150,000,000-175,000,000 |
انظر أيضاً
- Deflection
- Deformation
- Hardness
- Hooke's law
- Shear modulus
- Impulse excitation technique
- Strain
- Stress
- Toughness
- Yield (engineering)
- List of materials properties
المصادر
- ^ The Rational Mechanics of Flexible or Elastic Bodies, 1638-1788: Introduction to Leonhardi Euleri Opera Omnia, vol. X and XI, Seriei Secundae. Orell Fussli.
- ^ The Rational mechanics of Flexible or Elastic Bodies, 1638–1788: Introduction to Leonhardi Euleri Opera Omnia, vol. X and XI, Seriei Secundae. Orell Fussli.
- ^ Jastrzebski, D. (1959). Nature and Properties of Engineering Materials (Wiley International ed.). John Wiley & Sons, Inc.
- ^ Tilleman, Tamara Raveh; Tilleman, Michael M.; Neumann, Martino H.A. (December 2004). "The Elastic Properties of Cancerous Skin: Poisson's Ratio and Young's Modulus" (PDF). Israel Medical Association Journal. 6 (12): 753–755.
- ^ Gorodtsov, V.A.; Lisovenko, D.S. (2019). "Extreme values of Young's modulus and Poisson's ratio of hexagonal crystals". Mechanics of Materials (in الإنجليزية). 134: 1–8. doi:10.1016/j.mechmat.2019.03.017. S2CID 140493258.
- ^ Rahemi, Reza; Li, Dongyang (April 2015). "Variation in electron work function with temperature and its effect on the Young's modulus of metals". Scripta Materialia. 99 (2015): 41–44. arXiv:1503.08250. Bibcode:2015arXiv150308250R. doi:10.1016/j.scriptamat.2014.11.022. S2CID 118420968.
- ^ http://www.engineeringtoolbox.com/young-modulus-d_417.html
- ^ Glassproperties.com
وصلات خارجية
| صيغ التحويل | |||||||
|---|---|---|---|---|---|---|---|
| Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas. | |||||||
| Notes | |||||||
There are two valid solutions. | |||||||
| Cannot be used when | |||||||















































































































