خوارزمية إقليدس

خوارزمية إقليدس في نظرية الأعداد هي خوارزمية لحساب القاسم المشترك الأكبر لعددين طبيعيين ، تظهر أهميتها الأساسية في عدم حاجتنا لتحليل الرقمين كي نتمكن من حساب القاسم المشترك الأكبر لهما ، وتتميز بكونها إحدى أقدم الخوارزميات حيث ترجع إلى سنة 300 ق.م. .
وصف الخوارزمية
القاسم المشترك الأكبر لعددين طبيعيين A ، B يساوي القاسم المشترك الأكبر للعدد الثاني B و باقي قسمة A على B ، ونكرر العملية نفسها حتى يصبح باقي القسمة مساويا الصفر ، عندئذ يكون القاسم المشترك الأكبر هو العدد الآخر.
حيث :
r باقي قسمة A على B
N هو القاسم المشترك الأكبر.
مثال
القاسم المشترك الأكبر للعددين 252 و 198 :
252 = 198 * 1 + 54 ‘ أربع وخمسون هو باقي قسمة 252 على 198
فنجد القاسم المشترك للعددين 198 و 54
198 = 54 * 3 + 36 ‘ ست وثلاثون هو باقي القسمة.
نكرر العملية هذه المرة مع : 54 و 36
54 = 36 * 1 + 18
مرة أخرى : 36 = 18 * 2 + 0
هنا وصلنا للصفر فيكون العدد الثاني 18 هو القاسم المشترك الأكبر.
خلفية: القاسم المشترك الأعظم
The Euclidean algorithm calculates the greatest common divisor (GCD) of two natural numbers a and b. The greatest common divisor g is the largest natural number that divides both a and b without leaving a remainder. Synonyms for GCD include greatest common factor (GCF), highest common factor (HCF), highest common divisor (HCD), and greatest common measure (GCM). The greatest common divisor is often written as gcd(a, b) or, more simply, as (a, b),[1] although the latter notation is ambiguous, also used for concepts such as an ideal in the ring of integers, which is closely related to GCD.
If gcd(a, b) = 1, then a and b are said to be coprime (or relatively prime).[2] This property does not imply that a or b are themselves prime numbers.[3] For example, 6 and 35 factor as 6 = 2 × 3 and 35 = 5 × 7, so they are not prime, but their prime factors are different, so 6 and 35 are coprime, with no common factors other than 1.
Let g = gcd(a, b). Since a and b are both multiples of g, they can be written a = mg and b = ng, and there is no larger number G > g for which this is true. The natural numbers m and n must be coprime, since any common factor could be factored out of m and n to make g greater. Thus, any other number c that divides both a and b must also divide g. The greatest common divisor g of a and b is the unique (positive) common divisor of a and b that is divisible by any other common divisor c.[4]
The greatest common divisor can be visualized as follows.[5] Consider a rectangular area a by b, and any common divisor c that divides both a and b exactly. The sides of the rectangle can be divided into segments of length c, which divides the rectangle into a grid of squares of side length c. The GCD g is the largest value of c for which this is possible. For illustration, a 24×60 rectangular area can be divided into a grid of: 1×1 squares, 2×2 squares, 3×3 squares, 4×4 squares, 6×6 squares or 12×12 squares. Therefore, 12 is the GCD of 24 and 60. A 24×60 rectangular area can be divided into a grid of 12×12 squares, with two squares along one edge (24/12 = 2) and five squares along the other (60/12 = 5).
The greatest common divisor of two numbers a and b is the product of the prime factors shared by the two numbers, where each prime factor can be repeated as many times as it divides both a and b.[6] For example, since 1386 can be factored into 2 × 3 × 3 × 7 × 11, and 3213 can be factored into 3 × 3 × 3 × 7 × 17, the GCD of 1386 and 3213 equals 63 = 3 × 3 × 7, the product of their shared prime factors (with 3 repeated since 3 × 3 divides both). If two numbers have no common prime factors, their GCD is 1 (obtained here as an instance of the empty product); in other words, they are coprime. A key advantage of the Euclidean algorithm is that it can find the GCD efficiently without having to compute the prime factors.[7][8] Factorization of large integers is believed to be a computationally very difficult problem, and the security of many widely used cryptographic protocols is based upon its infeasibility.[9]
Another definition of the GCD is helpful in advanced mathematics, particularly ring theory.[10] The greatest common divisor g of two nonzero numbers a and b is also their smallest positive integral linear combination, that is, the smallest positive number of the form ua + vb where u and v are integers. The set of all integral linear combinations of a and b is actually the same as the set of all multiples of g (mg, where m is an integer). In modern mathematical language, the ideal generated by a and b is the ideal generated by g alone (an ideal generated by a single element is called a principal ideal, and all ideals of the integers are principal ideals). Some properties of the GCD are in fact easier to see with this description, for instance the fact that any common divisor of a and b also divides the GCD (it divides both terms of ua + vb). The equivalence of this GCD definition with the other definitions is described below.
The GCD of three or more numbers equals the product of the prime factors common to all the numbers,[11] but it can also be calculated by repeatedly taking the GCDs of pairs of numbers.[12] For example,
- gcd(a, b, c) = gcd(a, gcd(b, c)) = gcd(gcd(a, b), c) = gcd(gcd(a, c), b).
Thus, Euclid's algorithm, which computes the GCD of two integers, suffices to calculate the GCD of arbitrarily many integers.
العملية
قالب:Euclidean algorithm steps The Euclidean algorithm can be thought of as constructing a sequence of non-negative integers that begins with the two given integers and and will eventually terminate with the integer zero: with . The integer will then be the GCD and we can state . The algorithm indicates how to construct the intermediate remainders via division-with-remainder on the preceding pair by finding an integer quotient so that:
Because the sequence of non-negative integers is strictly decreasing, it eventually must terminate. In other words, since for every , and each is an integer that is strictly smaller than the preceding , there eventually cannot be a non-negative integer smaller than zero, and hence the algorithm must terminate. In fact, the algorithm will always terminate at the nth step with equal to zero.[13]
To illustrate, suppose the GCD of 1071 and 462 is requested. The sequence is initially and in order to find , we need to find integers and such that:
- .
This is the quotient since . This determines and so the sequence is now . The next step is to continue the sequence to find by finding integers and such that:
- .
This is the quotient since . This determines and so the sequence is now . The next step is to continue the sequence to find by finding integers and such that:
- .
This is the quotient since . This determines and so the sequence is completed as as no further non-negative integer smaller than can be found. The penultimate remainder is therefore the requested GCD:
We can generalize slightly by dropping any ordering requirement on the initial two values and . If , the algorithm may continue and trivially find that as the sequence of remainders will be . If , then we can also continue since , suggesting the next remainder should be itself, and the sequence is . Normally, this would be invalid because it breaks the requirement but now we have by construction, so the requirement is automatically satisfied and the Euclidean algorithm can continue as normal. Therefore, dropping any ordering between the first two integers does not affect the conclusion that the sequence must eventually terminate because the next remainder will always satisfy and everything continues as above. The only modifications that need to be made are that only for , and that the sub-sequence of non-negative integers for is strictly decreasing, therefore excluding from both statements.
برهان الصحة
The validity of the Euclidean algorithm can be proven by a two-step argument.[14] In the first step, the final nonzero remainder rN−1 is shown to divide both a and b. Since it is a common divisor, it must be less than or equal to the greatest common divisor g. In the second step, it is shown that any common divisor of a and b, including g, must divide rN−1; therefore, g must be less than or equal to rN−1. These two opposite inequalities imply rN−1 = g.
To demonstrate that rN−1 divides both a and b (the first step), rN−1 divides its predecessor rN−2
- rN−2 = qN rN−1
since the final remainder rN is zero. rN−1 also divides its next predecessor rN−3
- rN−3 = qN−1 rN−2 + rN−1
because it divides both terms on the right-hand side of the equation. Iterating the same argument, rN−1 divides all the preceding remainders, including a and b. None of the preceding remainders rN−2, rN−3, etc. divide a and b, since they leave a remainder. Since rN−1 is a common divisor of a and b, rN−1 ≤ g.
In the second step, any natural number c that divides both a and b (in other words, any common divisor of a and b) divides the remainders rk. By definition, a and b can be written as multiples of c: a = mc and b = nc, where m and n are natural numbers. Therefore, c divides the initial remainder r0, since r0 = a − q0b = mc − q0nc = (m − q0n)c. An analogous argument shows that c also divides the subsequent remainders r1, r2, etc. Therefore, the greatest common divisor g must divide rN−1, which implies that g ≤ rN−1. Since the first part of the argument showed the reverse (rN−1 ≤ g), it follows that g = rN−1. Thus, g is the greatest common divisor of all the succeeding pairs:[15][16]
مثال محلول

For illustration, the Euclidean algorithm can be used to find the greatest common divisor of a = 1071 and b = 462. To begin, multiples of 462 are subtracted from 1071 until the remainder is less than 462. Two such multiples can be subtracted (q0 = 2), leaving a remainder of 147:
- 1071 = 2 × 462 + 147.
Then multiples of 147 are subtracted from 462 until the remainder is less than 147. Three multiples can be subtracted (q1 = 3), leaving a remainder of 21:
- 462 = 3 × 147 + 21.
Then multiples of 21 are subtracted from 147 until the remainder is less than 21. Seven multiples can be subtracted (q2 = 7), leaving no remainder:
- 147 = 7 × 21 + 0.
Since the last remainder is zero, the algorithm ends with 21 as the greatest common divisor of 1071 and 462. This agrees with the gcd(1071, 462) found by prime factorization above. In tabular form, the steps are:
| Step k | Equation | Quotient and remainder |
|---|---|---|
| 0 | 1071 = q0 462 + r0 | q0 = 2 and r0 = 147 |
| 1 | 462 = q1 147 + r1 | q1 = 3 and r1 = 21 |
| 2 | 147 = q2 21 + r2 | q2 = 7 and r2 = 0; algorithm ends |
التصور
The Euclidean algorithm can be visualized in terms of the tiling analogy given above for the greatest common divisor.[17] Assume that we wish to cover an a×b rectangle with square tiles exactly, where a is the larger of the two numbers. We first attempt to tile the rectangle using b×b square tiles; however, this leaves an r0×b residual rectangle untiled, where r0 < b. We then attempt to tile the residual rectangle with r0×r0 square tiles. This leaves a second residual rectangle r1×r0, which we attempt to tile using r1×r1 square tiles, and so on. The sequence ends when there is no residual rectangle, i.e., when the square tiles cover the previous residual rectangle exactly. The length of the sides of the smallest square tile is the GCD of the dimensions of the original rectangle. For example, the smallest square tile in the adjacent figure is 21×21 (shown in red), and 21 is the GCD of 1071 and 462, the dimensions of the original rectangle (shown in green).
القسمة الإقليدية
At every step k, the Euclidean algorithm computes a quotient qk and remainder rk from two numbers rk−1 and rk−2
- rk−2 = qk rk−1 + rk,
where the rk is non-negative and is strictly less than the absolute value of rk−1. The theorem which underlies the definition of the Euclidean division ensures that such a quotient and remainder always exist and are unique.[18]
In Euclid's original version of the algorithm, the quotient and remainder are found by repeated subtraction; that is, rk−1 is subtracted from rk−2 repeatedly until the remainder rk is smaller than rk−1. After that rk and rk−1 are exchanged and the process is iterated. Euclidean division reduces all the steps between two exchanges into a single step, which is thus more efficient. Moreover, the quotients are not needed, thus one may replace Euclidean division by the modulo operation, which gives only the remainder. Thus the iteration of the Euclidean algorithm becomes simply
- rk = rk−2 mod rk−1.
تنفيذات
Implementations of the algorithm may be expressed in pseudocode. For example, the division-based version may be programmed as[19]
function gcd(a, b)
while b ≠ 0
t := b
b := a mod b
a := t
return a
At the beginning of the kth iteration, the variable b holds the latest remainder rk−1, whereas the variable a holds its predecessor, rk−2. The step b := a mod b is equivalent to the above recursion formula rk ≡ rk−2 mod rk−1. The temporary variable t holds the value of rk−1 while the next remainder rk is being calculated. At the end of the loop iteration, the variable b holds the remainder rk, whereas the variable a holds its predecessor, rk−1.
(If negative inputs are allowed, or if the mod function may return negative values, the last line must be replaced with return abs(a).)
In the subtraction-based version, which was Euclid's original version, the remainder calculation (b := a mod b) is replaced by repeated subtraction.[20] Contrary to the division-based version, which works with arbitrary integers as input, the subtraction-based version supposes that the input consists of positive integers and stops when a = b:
function gcd(a, b)
while a ≠ b
if a > b
a := a − b
else
b := b − a
return a
The variables a and b alternate holding the previous remainders rk−1 and rk−2. Assume that a is larger than b at the beginning of an iteration; then a equals rk−2, since rk−2 > rk−1. During the loop iteration, a is reduced by multiples of the previous remainder b until a is smaller than b. Then a is the next remainder rk. Then b is reduced by multiples of a until it is again smaller than a, giving the next remainder rk+1, and so on.
The recursive version[21] is based on the equality of the GCDs of successive remainders and the stopping condition gcd(rN−1, 0) = rN−1.
function gcd(a, b)
if b = 0
return a
else
return gcd(b, a mod b)
(As above, if negative inputs are allowed, or if the mod function may return negative values, the instruction return a must be replaced by return max(a, −a).)
For illustration, the gcd(1071, 462) is calculated from the equivalent gcd(462, 1071 mod 462) = gcd(462, 147). The latter GCD is calculated from the gcd(147, 462 mod 147) = gcd(147, 21), which in turn is calculated from the gcd(21, 147 mod 21) = gcd(21, 0) = 21.
طريقة أقل باقي مطلق
In another version of Euclid's algorithm, the quotient at each step is increased by one if the resulting negative remainder is smaller in magnitude than the typical positive remainder.[22][23] Previously, the equation
- rk−2 = qk rk−1 + rk
assumed that |rk−1| > rk > 0. However, an alternative negative remainder ek can be computed:
- rk−2 = (qk + 1) rk−1 + ek
if rk−1 > 0 or
- rk−2 = (qk – 1) rk−1 + ek
if rk−1 < 0.
If rk is replaced by ek. when |ek| < |rk|, then one gets a variant of Euclidean algorithm such that
- |rk| ≤ |rk−1| / 2
at each step.
Leopold Kronecker has shown that this version requires the fewest steps of any version of Euclid's algorithm.[22][23] More generally, it has been proven that, for every input numbers a and b, the number of steps is minimal if and only if qk is chosen in order that where is the golden ratio.[24]
Historical development
The Euclidean algorithm is one of the oldest algorithms in common use.[25] It appears in Euclid's Elements (c. 300 BC), specifically in Book 7 (Propositions 1–2) and Book 10 (Propositions 2–3). In Book 7, the algorithm is formulated for integers, whereas in Book 10, it is formulated for lengths of line segments. (In modern usage, one would say it was formulated there for real numbers. But lengths, areas, and volumes, represented as real numbers in modern usage, are not measured in the same units and there is no natural unit of length, area, or volume; the concept of real numbers was unknown at that time.) The latter algorithm is geometrical. The GCD of two lengths a and b corresponds to the greatest length g that measures a and b evenly; in other words, the lengths a and b are both integer multiples of the length g.
The algorithm was probably not discovered by Euclid, who compiled results from earlier mathematicians in his Elements.[26][27] The mathematician and historian B. L. van der Waerden suggests that Book VII derives from a textbook on number theory written by mathematicians in the school of Pythagoras.[28] The algorithm was probably known by Eudoxus of Cnidus (about 375 BC).[25][29] The algorithm may even pre-date Eudoxus,[30][31] judging from the use of the technical term ἀνθυφαίρεσις (anthyphairesis, reciprocal subtraction) in works by Euclid and Aristotle.[32] Claude Brezinski, following remarks by Pappus of Alexandria, credits the algorithm to Theaetetus (c. 417 – c. 369 BC).[33]
Centuries later, Euclid's algorithm was discovered independently both in India and in China,[34] primarily to solve Diophantine equations that arose in astronomy and making accurate calendars. In the late 5th century, the Indian mathematician and astronomer Aryabhata described the algorithm as the "pulverizer",[35] perhaps because of its effectiveness in solving Diophantine equations.[36] Although a special case of the Chinese remainder theorem had already been described in the Chinese book Sunzi Suanjing,[37] the general solution was published by Qin Jiushao in his 1247 book Shushu Jiuzhang (數書九章 Mathematical Treatise in Nine Sections).[38] The Euclidean algorithm was first described numerically and popularized in Europe in the second edition of Bachet's Problèmes plaisants et délectables (Pleasant and enjoyable problems, 1624).[35] In Europe, it was likewise used to solve Diophantine equations and in developing continued fractions. The extended Euclidean algorithm was published by the English mathematician Nicholas Saunderson,[39] who attributed it to Roger Cotes as a method for computing continued fractions efficiently.[40]
In the 19th century, the Euclidean algorithm led to the development of new number systems, such as Gaussian integers and Eisenstein integers. In 1815, Carl Gauss used the Euclidean algorithm to demonstrate unique factorization of Gaussian integers, although his work was first published in 1832.[41] Gauss mentioned the algorithm in his Disquisitiones Arithmeticae (published 1801), but only as a method for continued fractions.[34] Peter Gustav Lejeune Dirichlet seems to have been the first to describe the Euclidean algorithm as the basis for much of number theory.[42] Lejeune Dirichlet noted that many results of number theory, such as unique factorization, would hold true for any other system of numbers to which the Euclidean algorithm could be applied.[43] Lejeune Dirichlet's lectures on number theory were edited and extended by Richard Dedekind, who used Euclid's algorithm to study algebraic integers, a new general type of number. For example, Dedekind was the first to prove Fermat's two-square theorem using the unique factorization of Gaussian integers.[44] Dedekind also defined the concept of a Euclidean domain, a number system in which a generalized version of the Euclidean algorithm can be defined (as described below). In the closing decades of the 19th century, the Euclidean algorithm gradually became eclipsed by Dedekind's more general theory of ideals.[45]
|
"[The Euclidean algorithm] is the granddaddy of all algorithms, because it is the oldest nontrivial algorithm that has survived to the present day." |
| Donald Knuth, The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 2nd edition (1981), p. 318. |
Other applications of Euclid's algorithm were developed in the 19th century. In 1829, Charles Sturm showed that the algorithm was useful in the Sturm chain method for counting the real roots of polynomials in any given interval.[46]
The Euclidean algorithm was the first integer relation algorithm, which is a method for finding integer relations between commensurate real numbers. Several novel integer relation algorithms have been developed, such as the algorithm of Helaman Ferguson and R.W. Forcade (1979)[47] and the LLL algorithm.[48][49]
In 1969, Cole and Davie developed a two-player game based on the Euclidean algorithm, called The Game of Euclid,[50] which has an optimal strategy.[51] The players begin with two piles of a and b stones. The players take turns removing m multiples of the smaller pile from the larger. Thus, if the two piles consist of x and y stones, where x is larger than y, the next player can reduce the larger pile from x stones to x − my stones, as long as the latter is a nonnegative integer. The winner is the first player to reduce one pile to zero stones.[52][53]
Mathematical applications
Bézout's identity
Bézout's identity states that the greatest common divisor g of two integers a and b can be represented as a linear sum of the original two numbers a and b.[54] In other words, it is always possible to find integers s and t such that g = sa + tb.[55][56]
The integers s and t can be calculated from the quotients q0, q1, etc. by reversing the order of equations in Euclid's algorithm.[57] Beginning with the next-to-last equation, g can be expressed in terms of the quotient qN−1 and the two preceding remainders, rN−2 and rN−3:
- g = rN−1 = rN−3 − qN−1 rN−2.
Those two remainders can be likewise expressed in terms of their quotients and preceding remainders,
- rN−2 = rN−4 − qN−2 rN−3 and
- rN−3 = rN−5 − qN−3 rN−4.
Substituting these formulae for rN−2 and rN−3 into the first equation yields g as a linear sum of the remainders rN−4 and rN−5. The process of substituting remainders by formulae involving their predecessors can be continued until the original numbers a and b are reached:
- r2 = r0 − q2 r1
- r1 = b − q1 r0
- r0 = a − q0 b.
After all the remainders r0, r1, etc. have been substituted, the final equation expresses g as a linear sum of a and b, so that g = sa + tb.
The Euclidean algorithm, and thus Bézout's identity, can be generalized to the context of Euclidean domains.
Bézout's identity provides yet another definition of the greatest common divisor g of two numbers a and b.[10] Consider the set of all numbers ua + vb, where u and v are any two integers. Since a and b are both divisible by g, every number in the set is divisible by g. In other words, every number of the set is an integer multiple of g. This is true for every common divisor of a and b. However, unlike other common divisors, the greatest common divisor is a member of the set; by Bézout's identity, choosing u = s and v = t gives g. A smaller common divisor cannot be a member of the set, since every member of the set must be divisible by g. Conversely, any multiple m of g can be obtained by choosing u = ms and v = mt, where s and t are the integers of Bézout's identity. This may be seen by multiplying Bézout's identity by m,
- mg = msa + mtb.
Therefore, the set of all numbers ua + vb is equivalent to the set of multiples m of g. In other words, the set of all possible sums of integer multiples of two numbers (a and b) is equivalent to the set of multiples of gcd(a, b). The GCD is said to be the generator of the ideal of a and b. This GCD definition led to the modern abstract algebraic concepts of a principal ideal (an ideal generated by a single element) and a principal ideal domain (a domain in which every ideal is a principal ideal).
Certain problems can be solved using this result.[58] For example, consider two measuring cups of volume a and b. By adding/subtracting u multiples of the first cup and v multiples of the second cup, any volume ua + vb can be measured out. These volumes are all multiples of g = gcd(a, b).
Extended Euclidean algorithm
The integers s and t of Bézout's identity can be computed efficiently using the extended Euclidean algorithm. This extension adds two recursive equations to Euclid's algorithm[59]
- sk = sk−2 − qksk−1
- tk = tk−2 − qktk−1
with the starting values
- s−2 = 1, t−2 = 0
- s−1 = 0, t−1 = 1.
Using this recursion, Bézout's integers s and t are given by s = sN and t = tN, where N + 1 is the step on which the algorithm terminates with rN+1 = 0.
The validity of this approach can be shown by induction. Assume that the recursion formula is correct up to step k − 1 of the algorithm; in other words, assume that
- rj = sj a + tj b
for all j less than k. The kth step of the algorithm gives the equation
- rk = rk−2 − qkrk−1.
Since the recursion formula has been assumed to be correct for rk−2 and rk−1, they may be expressed in terms of the corresponding s and t variables
- rk = (sk−2 a + tk−2 b) − qk(sk−1 a + tk−1 b).
Rearranging this equation yields the recursion formula for step k, as required
- rk = sk a + tk b = (sk−2 − qksk−1) a + (tk−2 − qktk−1) b.
Matrix method
The integers s and t can also be found using an equivalent matrix method.[60] The sequence of equations of Euclid's algorithm
can be written as a product of 2×2 quotient matrices multiplying a two-dimensional remainder vector
Let M represent the product of all the quotient matrices
This simplifies the Euclidean algorithm to the form
To express g as a linear sum of a and b, both sides of this equation can be multiplied by the inverse of the matrix M.[60][61] The determinant of M equals (−1)N+1, since it equals the product of the determinants of the quotient matrices, each of which is negative one. Since the determinant of M is never zero, the vector of the final remainders can be solved using the inverse of M
Since the top equation gives
- g = (−1)N+1 ( m22 a − m12 b),
the two integers of Bézout's identity are s = (−1)N+1m22 and t = (−1)Nm12. The matrix method is as efficient as the equivalent recursion, with two multiplications and two additions per step of the Euclidean algorithm.
Euclid's lemma and unique factorization
Bézout's identity is essential to many applications of Euclid's algorithm, such as demonstrating the unique factorization of numbers into prime factors.[62] To illustrate this, suppose that a number L can be written as a product of two factors u and v, that is, L = uv. If another number w also divides L but is coprime with u, then w must divide v, by the following argument: If the greatest common divisor of u and w is 1, then integers s and t can be found such that
- 1 = su + tw
by Bézout's identity. Multiplying both sides by v gives the relation:
- v = suv + twv = sL + twv
Since w divides both terms on the right-hand side, it must also divide the left-hand side, v. This result is known as Euclid's lemma.[63] Specifically, if a prime number divides L, then it must divide at least one factor of L. Conversely, if a number w is coprime to each of a series of numbers a1, a2, ..., an, then w is also coprime to their product, a1 × a2 × ... × an.[63]
Euclid's lemma suffices to prove that every number has a unique factorization into prime numbers.[64] To see this, assume the contrary, that there are two independent factorizations of L into m and n prime factors, respectively
- L = p1p2...pm = q1q2...qn .
Since each prime p divides L by assumption, it must also divide one of the q factors; since each q is prime as well, it must be that p = q. Iteratively dividing by the p factors shows that each p has an equal counterpart q; the two prime factorizations are identical except for their order. The unique factorization of numbers into primes has many applications in mathematical proofs, as shown below.
Linear Diophantine equations
Diophantine equations are equations in which the solutions are restricted to integers; they are named after the 3rd-century Alexandrian mathematician Diophantus.[65] A typical linear Diophantine equation seeks integers x and y such that[66]
- ax + by = c
where a, b and c are given integers. This can be written as an equation for x in modular arithmetic:
- ax ≡ c mod b.
Let g be the greatest common divisor of a and b. Both terms in ax + by are divisible by g; therefore, c must also be divisible by g, or the equation has no solutions. By dividing both sides by c/g, the equation can be reduced to Bezout's identity
- sa + tb = g,
where s and t can be found by the extended Euclidean algorithm.[67] This provides one solution to the Diophantine equation, x1 = s (c/g) and y1 = t (c/g).
In general, a linear Diophantine equation has no solutions, or an infinite number of solutions.[68] To find the latter, consider two solutions, (x1, y1) and (x2, y2), where
- ax1 + by1 = c = ax2 + by2
or equivalently
- a(x1 − x2) = b(y2 − y1).
Therefore, the smallest difference between two x solutions is b/g, whereas the smallest difference between two y solutions is a/g. Thus, the solutions may be expressed as
- x = x1 − bu/g
- y = y1 + au/g.
By allowing u to vary over all possible integers, an infinite family of solutions can be generated from a single solution (x1, y1). If the solutions are required to be positive integers (x > 0, y > 0), only a finite number of solutions may be possible. This restriction on the acceptable solutions allows some systems of Diophantine equations with more unknowns than equations to have a finite number of solutions;[69] this is impossible for a system of linear equations when the solutions can be any real number (see Underdetermined system).
Multiplicative inverses and the RSA algorithm
A finite field is a set of numbers with four generalized operations. The operations are called addition, subtraction, multiplication and division and have their usual properties, such as commutativity, associativity and distributivity. An example of a finite field is the set of 13 numbers {0, 1, 2, ..., 12} using modular arithmetic. In this field, the results of any mathematical operation (addition, subtraction, multiplication, or division) is reduced modulo 13; that is, multiples of 13 are added or subtracted until the result is brought within the range 0–12. For example, the result of 5 × 7 = 35 mod 13 = 9. Such finite fields can be defined for any prime p; using more sophisticated definitions, they can also be defined for any power m of a prime pm. Finite fields are often called Galois fields, and are abbreviated as GF(p) or GF(pm).
In such a field with m numbers, every nonzero element a has a unique modular multiplicative inverse, a−1 such that aa−1 = a−1a ≡ 1 mod m. This inverse can be found by solving the congruence equation ax ≡ 1 mod m,[70] or the equivalent linear Diophantine equation[71]
- ax + my = 1.
This equation can be solved by the Euclidean algorithm, as described above. Finding multiplicative inverses is an essential step in the RSA algorithm, which is widely used in electronic commerce; specifically, the equation determines the integer used to decrypt the message.[72] Although the RSA algorithm uses rings rather than fields, the Euclidean algorithm can still be used to find a multiplicative inverse where one exists. The Euclidean algorithm also has other applications in error-correcting codes; for example, it can be used as an alternative to the Berlekamp–Massey algorithm for decoding BCH and Reed–Solomon codes, which are based on Galois fields.[73]
Chinese remainder theorem
Euclid's algorithm can also be used to solve multiple linear Diophantine equations.[74] Such equations arise in the Chinese remainder theorem, which describes a novel method to represent an integer x. Instead of representing an integer by its digits, it may be represented by its remainders xi modulo a set of N coprime numbers mi:[75]
The goal is to determine x from its N remainders xi. The solution is to combine the multiple equations into a single linear Diophantine equation with a much larger modulus M that is the product of all the individual moduli mi, and define Mi as
Thus, each Mi is the product of all the moduli except mi. The solution depends on finding N new numbers hi such that
With these numbers hi, any integer x can be reconstructed from its remainders xi by the equation
Since these numbers hi are the multiplicative inverses of the Mi, they may be found using Euclid's algorithm as described in the previous subsection.
Stern–Brocot tree
The Euclidean algorithm can be used to arrange the set of all positive rational numbers into an infinite binary search tree, called the Stern–Brocot tree. The number 1 (expressed as a fraction 1/1) is placed at the root of the tree, and the location of any other number a/b can be found by computing gcd(a,b) using the original form of the Euclidean algorithm, in which each step replaces the larger of the two given numbers by its difference with the smaller number (not its remainder), stopping when two equal numbers are reached. A step of the Euclidean algorithm that replaces the first of the two numbers corresponds to a step in the tree from a node to its right child, and a step that replaces the second of the two numbers corresponds to a step in the tree from a node to its left child. The sequence of steps constructed in this way does not depend on whether a/b is given in lowest terms, and forms a path from the root to a node containing the number a/b.[76] This fact can be used to prove that each positive rational number appears exactly once in this tree.
For example, 3/4 can be found by starting at the root, going to the left once, then to the right twice:
The Euclidean algorithm has almost the same relationship to another binary tree on the rational numbers called the Calkin–Wilf tree. The difference is that the path is reversed: instead of producing a path from the root of the tree to a target, it produces a path from the target to the root.
Continued fractions
The Euclidean algorithm has a close relationship with continued fractions.[77] The sequence of equations can be written in the form
The last term on the right-hand side always equals the inverse of the left-hand side of the next equation. Thus, the first two equations may be combined to form
The third equation may be used to substitute the denominator term r1/r0, yielding
The final ratio of remainders rk/rk−1 can always be replaced using the next equation in the series, up to the final equation. The result is a continued fraction
In the worked example above, the gcd(1071, 462) was calculated, and the quotients qk were 2, 3 and 7, respectively. Therefore, the fraction 1071/462 may be written
as can be confirmed by calculation.
Factorization algorithms
Calculating a greatest common divisor is an essential step in several integer factorization algorithms,[78] such as Pollard's rho algorithm,[79] Shor's algorithm,[80] Dixon's factorization method[81] and the Lenstra elliptic curve factorization.[82] The Euclidean algorithm may be used to find this GCD efficiently. Continued fraction factorization uses continued fractions, which are determined using Euclid's algorithm.[83]
Algorithmic efficiency
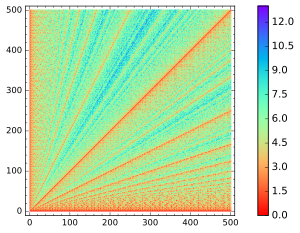
The computational efficiency of Euclid's algorithm has been studied thoroughly.[84] This efficiency can be described by the number of division steps the algorithm requires, multiplied by the computational expense of each step. The first known analysis of Euclid's algorithm is due to A. A. L. Reynaud in 1811,[85] who showed that the number of division steps on input (u, v) is bounded by v; later he improved this to v/2 + 2. Later, in 1841, P. J. E. Finck showed[86] that the number of division steps is at most 2 log2 v + 1, and hence Euclid's algorithm runs in time polynomial in the size of the input.[87] Émile Léger, in 1837, studied the worst case, which is when the inputs are consecutive Fibonacci numbers.[87] Finck's analysis was refined by Gabriel Lamé in 1844,[88] who showed that the number of steps required for completion is never more than five times the number h of base-10 digits of the smaller number b.[89][90]
In the uniform cost model (suitable for analyzing the complexity of gcd calculation on numbers that fit into a single machine word), each step of the algorithm takes constant time, and Lamé's analysis implies that the total running time is also O(h). However, in a model of computation suitable for computation with larger numbers, the computational expense of a single remainder computation in the algorithm can be as large as O(h2).[91] In this case the total time for all of the steps of the algorithm can be analyzed using a telescoping series, showing that it is also O(h2). Modern algorithmic techniques based on the Schönhage–Strassen algorithm for fast integer multiplication can be used to speed this up, leading to quasilinear algorithms for the GCD.[92][93]
Number of steps
The number of steps to calculate the GCD of two natural numbers, a and b, may be denoted by T(a, b).[94] If g is the GCD of a and b, then a = mg and b = ng for two coprime numbers m and n. Then
- T(a, b) = T(m, n)
as may be seen by dividing all the steps in the Euclidean algorithm by g.[95] By the same argument, the number of steps remains the same if a and b are multiplied by a common factor w: T(a, b) = T(wa, wb). Therefore, the number of steps T may vary dramatically between neighboring pairs of numbers, such as T(a, b) and T(a, b + 1), depending on the size of the two GCDs.
The recursive nature of the Euclidean algorithm gives another equation
- T(a, b) = 1 + T(b, r0) = 2 + T(r0, r1) = … = N + T(rN−2, rN−1) = N + 1
where T(x, 0) = 0 by assumption.[94]
Worst-case
If the Euclidean algorithm requires N steps for a pair of natural numbers a > b > 0, the smallest values of a and b for which this is true are the Fibonacci numbers FN+2 and FN+1, respectively.[96] More precisely, if the Euclidean algorithm requires N steps for the pair a > b, then one has a ≥ FN+2 and b ≥ FN+1. This can be shown by induction.[97] If N = 1, b divides a with no remainder; the smallest natural numbers for which this is true is b = 1 and a = 2, which are F2 and F3, respectively. Now assume that the result holds for all values of N up to M − 1. The first step of the M-step algorithm is a = q0b + r0, and the Euclidean algorithm requires M − 1 steps for the pair b > r0. By induction hypothesis, one has b ≥ FM+1 and r0 ≥ FM. Therefore, a = q0b + r0 ≥ b + r0 ≥ FM+1 + FM = FM+2, which is the desired inequality. This proof, published by Gabriel Lamé in 1844, represents the beginning of computational complexity theory,[98] and also the first practical application of the Fibonacci numbers.[96]
This result suffices to show that the number of steps in Euclid's algorithm can never be more than five times the number of its digits (base 10).[99] For if the algorithm requires N steps, then b is greater than or equal to FN+1 which in turn is greater than or equal to φN−1, where φ is the golden ratio. Since b ≥ φN−1, then N − 1 ≤ logφb. Since log10φ > 1/5, (N − 1)/5 < log10φ logφb = log10b. Thus, N ≤ 5 log10b. Thus, the Euclidean algorithm always needs less than O(h) divisions, where h is the number of digits in the smaller number b.
Average
The average number of steps taken by the Euclidean algorithm has been defined in three different ways. The first definition is the average time T(a) required to calculate the GCD of a given number a and a smaller natural number b chosen with equal probability from the integers 0 to a − 1[94]
However, since T(a, b) fluctuates dramatically with the GCD of the two numbers, the averaged function T(a) is likewise "noisy".[100]
To reduce this noise, a second average τ(a) is taken over all numbers coprime with a
There are φ(a) coprime integers less than a, where φ is Euler's totient function. This tau average grows smoothly with a[101][102]
with the residual error being of order a−(1/6)+ε, where ε is infinitesimal. The constant C in this formula is called Porter's constant[103] and equals
where γ is the Euler–Mascheroni constant and ζ′ is the derivative of the Riemann zeta function.[104][105] The leading coefficient (12/π2) ln 2 was determined by two independent methods.[106][107]
Since the first average can be calculated from the tau average by summing over the divisors d of a[108]
it can be approximated by the formula[109]
where Λ(d) is the Mangoldt function.[110]
A third average Y(n) is defined as the mean number of steps required when both a and b are chosen randomly (with uniform distribution) from 1 to n[109]
Substituting the approximate formula for T(a) into this equation yields an estimate for Y(n)[111]
Computational expense per step
In each step k of the Euclidean algorithm, the quotient qk and remainder rk are computed for a given pair of integers rk−2 and rk−1
- rk−2 = qk rk−1 + rk.
The computational expense per step is associated chiefly with finding qk, since the remainder rk can be calculated quickly from rk−2, rk−1, and qk
- rk = rk−2 − qk rk−1.
The computational expense of dividing h-bit numbers scales as O(h(ℓ + 1)), where ℓ is the length of the quotient.[91]
For comparison, Euclid's original subtraction-based algorithm can be much slower. A single integer division is equivalent to the quotient q number of subtractions. If the ratio of a and b is very large, the quotient is large and many subtractions will be required. On the other hand, it has been shown that the quotients are very likely to be small integers. The probability of a given quotient q is approximately ln |u/(u − 1)| where u = (q + 1)2.[112] For illustration, the probability of a quotient of 1, 2, 3, or 4 is roughly 41.5%, 17.0%, 9.3%, and 5.9%, respectively. Since the operation of subtraction is faster than division, particularly for large numbers,[113] the subtraction-based Euclid's algorithm is competitive with the division-based version.[114] This is exploited in the binary version of Euclid's algorithm.[115]
Combining the estimated number of steps with the estimated computational expense per step shows that the Euclid's algorithm grows quadratically (h2) with the average number of digits h in the initial two numbers a and b. Let h0, h1, ..., hN−1 represent the number of digits in the successive remainders r0, r1, ..., rN−1. Since the number of steps N grows linearly with h, the running time is bounded by
Alternative methods
Euclid's algorithm is widely used in practice, especially for small numbers, due to its simplicity.[116] For comparison, the efficiency of alternatives to Euclid's algorithm may be determined.
One inefficient approach to finding the GCD of two natural numbers a and b is to calculate all their common divisors; the GCD is then the largest common divisor. The common divisors can be found by dividing both numbers by successive integers from 2 to the smaller number b. The number of steps of this approach grows linearly with b, or exponentially in the number of digits. Another inefficient approach is to find the prime factors of one or both numbers. As noted above, the GCD equals the product of the prime factors shared by the two numbers a and b.[6] Present methods for prime factorization are also inefficient; many modern cryptography systems even rely on that inefficiency.[9]
The binary GCD algorithm is an efficient alternative that substitutes division with faster operations by exploiting the binary representation used by computers.[117][118] However, this alternative also scales like O(h²). It is generally faster than the Euclidean algorithm on real computers, even though it scales in the same way.[92] Additional efficiency can be gleaned by examining only the leading digits of the two numbers a and b.[119][120] The binary algorithm can be extended to other bases (k-ary algorithms),[121] with up to fivefold increases in speed.[122] Lehmer's GCD algorithm uses the same general principle as the binary algorithm to speed up GCD computations in arbitrary bases.
A recursive approach for very large integers (with more than 25,000 digits) leads to quasilinear integer GCD algorithms,[123] such as those of Schönhage,[124][125] and Stehlé and Zimmermann.[126] These algorithms exploit the 2×2 matrix form of the Euclidean algorithm given above. These quasilinear methods generally scale as O(h log h2 log log h).[92][93]
Generalizations
Although the Euclidean algorithm is used to find the greatest common divisor of two natural numbers (positive integers), it may be generalized to the real numbers, and to other mathematical objects, such as polynomials,[127] quadratic integers[128] and Hurwitz quaternions.[129] In the latter cases, the Euclidean algorithm is used to demonstrate the crucial property of unique factorization, i.e., that such numbers can be factored uniquely into irreducible elements, the counterparts of prime numbers. Unique factorization is essential to many proofs of number theory.
Rational and real numbers
Euclid's algorithm can be applied to real numbers, as described by Euclid in Book 10 of his Elements. The goal of the algorithm is to identify a real number g such that two given real numbers, a and b, are integer multiples of it: a = mg and b = ng, where m and n are integers.[26] This identification is equivalent to finding an integer relation among the real numbers a and b; that is, it determines integers s and t such that sa + tb = 0. If such an equation is possible, a and b are called commensurable lengths, otherwise they are incommensurable lengths.[130][131]
The real-number Euclidean algorithm differs from its integer counterpart in two respects. First, the remainders rk are real numbers, although the quotients qk are integers as before. Second, the algorithm is not guaranteed to end in a finite number N of steps. If it does, the fraction a/b is a rational number, i.e., the ratio of two integers
and can be written as a finite continued fraction [q0; q1, q2, ..., qN]. If the algorithm does not stop, the fraction a/b is an irrational number and can be described by an infinite continued fraction [q0; q1, q2, …].[132] Examples of infinite continued fractions are the golden ratio φ = [1; 1, 1, ...] and the square root of two, √2 = [1; 2, 2, ...].[133] When applied to two arbitrary real numbers, the algorithm is unlikely to stop, since almost all ratios a/b of two real numbers are irrational.[134]
An infinite continued fraction may be truncated at a step k [q0; q1, q2, ..., qk] to yield an approximation to a/b that improves as k is increased. The approximation is described by convergents mk/nk; the numerator and denominators are coprime and obey the recurrence relation
where m−1 = n−2 = 1 and m−2 = n−1 = 0 are the initial values of the recursion. The convergent mk/nk is the best rational number approximation to a/b with denominator nk:[135]
Polynomials
Polynomials in a single variable x can be added, multiplied and factored into irreducible polynomials, which are the analogs of the prime numbers for integers. The greatest common divisor polynomial g(x) of two polynomials a(x) and b(x) is defined as the product of their shared irreducible polynomials, which can be identified using the Euclidean algorithm.[127] The basic procedure is similar to that for integers. At each step k, a quotient polynomial qk(x) and a remainder polynomial rk(x) are identified to satisfy the recursive equation
where r−2(x) = a(x) and r−1(x) = b(x). Each quotient polynomial is chosen such that each remainder is either zero or has a degree that is smaller than the degree of its predecessor: deg[rk(x)] < deg[rk−1(x)]. Since the degree is a nonnegative integer, and since it decreases with every step, the Euclidean algorithm concludes in a finite number of steps. The last nonzero remainder is the greatest common divisor of the original two polynomials, a(x) and b(x).[136]
For example, consider the following two quartic polynomials, which each factor into two quadratic polynomials
Dividing a(x) by b(x) yields a remainder r0(x) = x3 + (2/3)x2 + (5/3)x − (2/3). In the next step, b(x) is divided by r0(x) yielding a remainder r1(x) = x2 + x + 2. Finally, dividing r0(x) by r1(x) yields a zero remainder, indicating that r1(x) is the greatest common divisor polynomial of a(x) and b(x), consistent with their factorization.
Many of the applications described above for integers carry over to polynomials.[137] The Euclidean algorithm can be used to solve linear Diophantine equations and Chinese remainder problems for polynomials; continued fractions of polynomials can also be defined.
The polynomial Euclidean algorithm has other applications, such as Sturm chains, a method for counting the zeros of a polynomial that lie inside a given real interval.[138] This in turn has applications in several areas, such as the Routh–Hurwitz stability criterion in control theory.[139]
Finally, the coefficients of the polynomials need not be drawn from integers, real numbers or even the complex numbers. For example, the coefficients may be drawn from a general field, such as the finite fields GF(p) described above. The corresponding conclusions about the Euclidean algorithm and its applications hold even for such polynomials.[127]
Gaussian integers
The Gaussian integers are complex numbers of the form α = u + vi, where u and v are ordinary integers[note 1] and i is the square root of negative one.[140] By defining an analog of the Euclidean algorithm, Gaussian integers can be shown to be uniquely factorizable, by the argument above.[41] This unique factorization is helpful in many applications, such as deriving all Pythagorean triples or proving Fermat's theorem on sums of two squares.[140] In general, the Euclidean algorithm is convenient in such applications, but not essential; for example, the theorems can often be proven by other arguments.
The Euclidean algorithm developed for two Gaussian integers α and β is nearly the same as that for ordinary integers,[141] but differs in two respects. As before, we set r−2 = α and r−1 = β, and the task at each step k is to identify a quotient qk and a remainder rk such that
where every remainder is strictly smaller than its predecessor: قالب:Mabs < قالب:Mabs. The first difference is that the quotients and remainders are themselves Gaussian integers, and thus are complex numbers. The quotients qk are generally found by rounding the real and complex parts of the exact ratio (such as the complex number α/β) to the nearest integers.[141] The second difference lies in the necessity of defining how one complex remainder can be "smaller" than another. To do this, a norm function f(u + vi) = u2 + v2 is defined, which converts every Gaussian integer u + vi into an ordinary integer. After each step k of the Euclidean algorithm, the norm of the remainder f(rk) is smaller than the norm of the preceding remainder, f(rk−1). Since the norm is a nonnegative integer and decreases with every step, the Euclidean algorithm for Gaussian integers ends in a finite number of steps.[142] The final nonzero remainder is gcd(α, β), the Gaussian integer of largest norm that divides both α and β; it is unique up to multiplication by a unit, ±1 or ±i.[143]
Many of the other applications of the Euclidean algorithm carry over to Gaussian integers. For example, it can be used to solve linear Diophantine equations and Chinese remainder problems for Gaussian integers;[144] continued fractions of Gaussian integers can also be defined.[141]
Euclidean domains
A set of elements under two binary operations, denoted as addition and multiplication, is called a Euclidean domain if it forms a commutative ring R and, roughly speaking, if a generalized Euclidean algorithm can be performed on them.[145][146] The two operations of such a ring need not be the addition and multiplication of ordinary arithmetic; rather, they can be more general, such as the operations of a mathematical group or monoid. Nevertheless, these general operations should respect many of the laws governing ordinary arithmetic, such as commutativity, associativity and distributivity.
The generalized Euclidean algorithm requires a Euclidean function, i.e., a mapping f from R into the set of nonnegative integers such that, for any two nonzero elements a and b in R, there exist q and r in R such that a = qb + r and f(r) < f(b).[147] Examples of such mappings are the absolute value for integers, the degree for univariate polynomials, and the norm for Gaussian integers above.[148][149] The basic principle is that each step of the algorithm reduces f inexorably; hence, if f can be reduced only a finite number of times, the algorithm must stop in a finite number of steps. This principle relies on the well-ordering property of the non-negative integers, which asserts that every non-empty set of non-negative integers has a smallest member.[150]
The fundamental theorem of arithmetic applies to any Euclidean domain: Any number from a Euclidean domain can be factored uniquely into irreducible elements. Any Euclidean domain is a unique factorization domain (UFD), although the converse is not true.[150] The Euclidean domains and the UFD's are subclasses of the GCD domains, domains in which a greatest common divisor of two numbers always exists.[151] In other words, a greatest common divisor may exist (for all pairs of elements in a domain), although it may not be possible to find it using a Euclidean algorithm. A Euclidean domain is always a principal ideal domain (PID), an integral domain in which every ideal is a principal ideal.[152] Again, the converse is not true: not every PID is a Euclidean domain.
The unique factorization of Euclidean domains is useful in many applications. For example, the unique factorization of the Gaussian integers is convenient in deriving formulae for all Pythagorean triples and in proving Fermat's theorem on sums of two squares.[140] Unique factorization was also a key element in an attempted proof of Fermat's Last Theorem published in 1847 by Gabriel Lamé, the same mathematician who analyzed the efficiency of Euclid's algorithm, based on a suggestion of Joseph Liouville.[153] Lamé's approach required the unique factorization of numbers of the form x + ωy, where x and y are integers, and ω = e2iπ/n is an nth root of 1, that is, ωn = 1. Although this approach succeeds for some values of n (such as n = 3, the Eisenstein integers), in general such numbers do not factor uniquely. This failure of unique factorization in some cyclotomic fields led Ernst Kummer to the concept of ideal numbers and, later, Richard Dedekind to ideals.[154]
Unique factorization of quadratic integers

The quadratic integer rings are helpful to illustrate Euclidean domains. Quadratic integers are generalizations of the Gaussian integers in which the imaginary unit i is replaced by a number ω. Thus, they have the form u + vω, where u and v are integers and ω has one of two forms, depending on a parameter D. If D does not equal a multiple of four plus one, then
If, however, D does equal a multiple of four plus one, then
If the function f corresponds to a norm function, such as that used to order the Gaussian integers above, then the domain is known as norm-Euclidean. The norm-Euclidean rings of quadratic integers are exactly those where D is one of the values −11, −7, −3, −2, −1, 2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29, 33, 37, 41, 57, or 73.[155][156] The cases D = −1 and D = −3 yield the Gaussian integers and Eisenstein integers, respectively.
If f is allowed to be any Euclidean function, then the list of possible values of D for which the domain is Euclidean is not yet known.[157] The first example of a Euclidean domain that was not norm-Euclidean (with D = 69) was published in 1994.[157] In 1973, Weinberger proved that a quadratic integer ring with D > 0 is Euclidean if, and only if, it is a principal ideal domain, provided that the generalized Riemann hypothesis holds.[128]
Noncommutative rings
The Euclidean algorithm may be applied to some noncommutative rings such as the set of Hurwitz quaternions.[129][158] Let α and β represent two elements from such a ring. They have a common right divisor δ if α = ξδ and β = ηδ for some choice of ξ and η in the ring. Similarly, they have a common left divisor if α = dξ and β = dη for some choice of ξ and η in the ring. Since multiplication is not commutative, there are two versions of the Euclidean algorithm, one for right divisors and one for left divisors.[129][158] Choosing the right divisors, the first step in finding the gcd(α, β) by the Euclidean algorithm can be written
where ψ0 represents the quotient and ρ0 the remainder. Here the quotient and remainder are chosen so that (if nonzero) the remainder has N(ρ0) < N(β) for a "Euclidean function" N defined analogously to the Euclidean functions of Euclidean domains in the non-commutative case.[158] This equation shows that any common right divisor of α and β is likewise a common divisor of the remainder ρ0. The analogous equation for the left divisors would be
With either choice, the process is repeated as above until the greatest common right or left divisor is identified. As in the Euclidean domain, the "size" of the remainder ρ0 (formally, its Euclidean function or "norm") must be strictly smaller than β, and there must be only a finite number of possible sizes for ρ0, so that the algorithm is guaranteed to terminate.[159]
Many results for the GCD carry over to noncommutative numbers. For example, Bézout's identity states that the right gcd(α, β) can be expressed as a linear combination of α and β.[160] In other words, there are numbers σ and τ such that
The analogous identity for the left GCD is nearly the same:
Bézout's identity can be used to solve Diophantine equations. For instance, one of the standard proofs of Lagrange's four-square theorem, that every positive integer can be represented as a sum of four squares, is based on quaternion GCDs in this way.[159]
خوارزمية إقليدس بلغة الحاسوب
التعليمات المطلوبة لتنفيذ خوارزمية إقليدس التي تقبل 0 على إي من مدخلاتها هي الحصول على القيمة المطلقة والتعيين والاختبارات النطقية والاستبدال والتكرار والطرح.
هذه الفقرة مازالت تحت الإنشاء!
انظر أيضاً
- Euclidean rhythm, a method for using the Euclidean algorithm to generate musical rhythms
Notes
- ^ The phrase "ordinary integer" is commonly used for distinguishing usual integers from Gaussian integers, and more generally from algebraic integers.
References
- ^ Stark 1978, p. 16
- ^ Stark 1978, p. 21
- ^ LeVeque 1996, p. 32
- ^ LeVeque 1996, p. 31
- ^ Grossman, J. W. (1990). Discrete Mathematics. New York: Macmillan. p. 213. ISBN 0-02-348331-8.
- ^ أ ب Schroeder 2005, pp. 21–22
- ^ Schroeder 2005, p. 19
- ^ Ogilvy, C. S.; Anderson, J. T. (1966). Excursions in number theory. New York: Oxford University Press. pp. 27–29.
- ^ أ ب Schroeder 2005, pp. 216–219
- ^ أ ب LeVeque 1996, p. 33
- ^ Stark 1978, p. 25
- ^ Ore 1948, pp. 47–48
- ^ Stark 1978, p. 18
- ^ Stark 1978, pp. 16–20
- ^ Knuth 1997, p. 320
- ^ Lovász, L.; Pelikán, J.; Vesztergombi, K. (2003). Discrete Mathematics: Elementary and Beyond. New York: Springer-Verlag. pp. 100–101. ISBN 0-387-95584-4.
- ^ Kimberling, C. (1983). "A Visual Euclidean Algorithm". Mathematics Teacher. 76: 108–109.
- ^ Dummit, David S.; Foote, Richard M. (2004). Abstract Algebra. John Wiley & Sons, Inc. pp. 270–271. ISBN 978-0-471-43334-7.
- ^ Knuth 1997, pp. 319–320
- ^ Knuth 1997, pp. 318–319
- ^ Stillwell 1997, p. 14
- ^ أ ب Ore 1948, p. 43
- ^ أ ب Stewart, B. M. (1964). Theory of Numbers (2nd ed.). New York: Macmillan. pp. 43–44. LCCN 64010964.
- ^ Lazard, D. (1977). "Le meilleur algorithme d'Euclide pour K[X] et Z". Comptes Rendus de l'Académie des Sciences (in الفرنسية). 284: 1–4.
- ^ أ ب Knuth 1997, p. 318
- ^ أ ب Weil, A. (1983). Number Theory. Boston: Birkhäuser. pp. 4–6. ISBN 0-8176-3141-0.
- ^ Jones, A. (1994). "Greek mathematics to AD 300". Companion encyclopedia of the history and philosophy of the mathematical sciences. New York: Routledge. pp. 46–48. ISBN 0-415-09238-8.
- ^ van der Waerden, B. L. (1954). Science Awakening. translated by Arnold Dresden. Groningen: P. Noordhoff Ltd. pp. 114–115.
- ^ von Fritz, K. (1945). "The Discovery of Incommensurability by Hippasus of Metapontum". Annals of Mathematics. 46 (2): 242–264. doi:10.2307/1969021. JSTOR 1969021.
- ^ Heath, T. L. (1949). Mathematics in Aristotle. Oxford Press. pp. 80–83.
- ^ Fowler, D. H. (1987). The Mathematics of Plato's Academy: A New Reconstruction. Oxford: Oxford University Press. pp. 31–66. ISBN 0-19-853912-6.
- ^ Becker, O. (1933). "Eudoxus-Studien I. Eine voreuklidische Proportionslehre und ihre Spuren bei Aristoteles und Euklid". Quellen und Studien zur Geschichte der Mathematik B. 2: 311–333.
- ^ Brezinski, Claude (1991). History of continued fractions and Padé approximants. Springer Series in Computational Mathematics. Vol. 12. Springer-Verlag, Berlin. p. 6. doi:10.1007/978-3-642-58169-4. ISBN 3-540-15286-5. MR 1083352.
- ^ أ ب Stillwell 1997, p. 31
- ^ أ ب Tattersall 2005, p. 70
- ^ Rosen 2000, pp. 86–87
- ^ Ore 1948, pp. 247–248
- ^ Tattersall 2005, pp. 72, 184–185
- ^ Saunderson, Nicholas (1740). The Elements of Algebra in Ten Books. University of Cambridge Press. Retrieved 1 November 2016.
- ^ Tattersall 2005, pp. 72–76
- ^ أ ب Gauss, C. F. (1832). "Theoria residuorum biquadraticorum". Comm. Soc. Reg. Sci. Gött. Rec. 4. Reprinted in Gauss, C. F. (2011). "Theoria residuorum biquadraticorum commentatio prima". Werke. Vol. 2. Cambridge Univ. Press. pp. 65–92. doi:10.1017/CBO9781139058230.004. ISBN 9781139058230. and Gauss, C. F. (2011). "Theoria residuorum biquadraticorum commentatio secunda". Werke. Vol. 2. Cambridge Univ. Press. pp. 93–148. doi:10.1017/CBO9781139058230.005. ISBN 9781139058230.
- ^ Stillwell 1997, pp. 31–32
- ^ Lejeune Dirichlet 1894, pp. 29–31
- ^ Richard Dedekind in Lejeune Dirichlet 1894, Supplement XI
- ^ Stillwell 2003, pp. 41–42
- ^ Sturm, C. (1829). "Mémoire sur la résolution des équations numériques". Bull. Des sciences de Férussac (in الفرنسية). 11: 419–422.
- ^ Ferguson, H. R. P.; Forcade, R. W. (1979). "Generalization of the Euclidean algorithm for real numbers to all dimensions higher than two". Bulletin of the American Mathematical Society. New Series. 1 (6): 912–914. doi:10.1090/S0273-0979-1979-14691-3. MR 0546316.
- ^ Peterson, I. (12 August 2002). "Jazzing Up Euclid's Algorithm". ScienceNews.
- ^ Cipra, Barry Arthur (16 مايو 2000). "The Best of the 20th Century: Editors Name Top 10 Algorithms" (PDF). SIAM News. Society for Industrial and Applied Mathematics. 33 (4). Archived from the original (PDF) on 22 سبتمبر 2016. Retrieved 19 يوليو 2016.
- ^ Cole, A. J.; Davie, A. J. T. (1969). "A game based on the Euclidean algorithm and a winning strategy for it". Math. Gaz. 53 (386): 354–357. doi:10.2307/3612461. JSTOR 3612461. S2CID 125164797.
- ^ Spitznagel, E. L. (1973). "Properties of a game based on Euclid's algorithm". Math. Mag. 46 (2): 87–92. doi:10.2307/2689037. JSTOR 2689037.
- ^ Rosen 2000, p. 95
- ^ Roberts, J. (1977). Elementary Number Theory: A Problem Oriented Approach. Cambridge, MA: MIT Press. pp. 1–8. ISBN 0-262-68028-9.
- ^ Jones, G. A.; Jones, J. M. (1998). "Bezout's Identity". Elementary Number Theory. New York: Springer-Verlag. pp. 7–11.
- ^ Rosen 2000, p. 81
- ^ Cohn 1980, p. 104
- ^ Rosen 2000, p. 91
- ^ Schroeder 2005, p. 23
- ^ Rosen 2000, pp. 90–93
- ^ أ ب Koshy, T. (2002). Elementary Number Theory with Applications. Burlington, MA: Harcourt/Academic Press. pp. 167–169. ISBN 0-12-421171-2.
- ^ Bach, E.; Shallit, J. (1996). Algorithmic number theory. Cambridge, MA: MIT Press. pp. 70–73. ISBN 0-262-02405-5.
- ^ Stark 1978, pp. 26–36
- ^ أ ب Ore 1948, p. 44
- ^ Stark 1978, pp. 281–292
- ^ Rosen 2000, pp. 119–125
- ^ Schroeder 2005, pp. 106–107
- ^ Schroeder 2005, pp. 108–109
- ^ Rosen 2000, pp. 120–121
- ^ Stark 1978, p. 47
- ^ Schroeder 2005, pp. 107–109
- ^ Stillwell 1997, pp. 186–187
- ^ Schroeder 2005, p. 134
- ^ Moon, T. K. (2005). Error Correction Coding: Mathematical Methods and Algorithms. John Wiley and Sons. p. 266. ISBN 0-471-64800-0.
- ^ Rosen 2000, pp. 143–170
- ^ Schroeder 2005, pp. 194–195
- ^ Graham, R.; Knuth, D. E.; Patashnik, O. (1989). Concrete mathematics. Addison-Wesley. p. 123.
- ^ Vinogradov, I. M. (1954). Elements of Number Theory. New York: Dover. pp. 3–13.
- ^ Crandall & Pomerance 2001, pp. 225–349
- ^ Knuth 1997, pp. 369–371
- ^ Shor, P. W. (1997). "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer". SIAM Journal on Scientific and Statistical Computing. 26 (5): 1484–1509. arXiv:quant-ph/9508027. Bibcode:1995quant.ph..8027S. doi:10.1137/s0097539795293172. S2CID 2337707.
- ^ Dixon, J. D. (1981). "Asymptotically fast factorization of integers". Math. Comput. 36 (153): 255–260. doi:10.2307/2007743. JSTOR 2007743.
- ^ Lenstra, H. W. Jr. (1987). "Factoring integers with elliptic curves". Annals of Mathematics. 126 (3): 649–673. doi:10.2307/1971363. hdl:1887/2140. JSTOR 1971363.
- ^ Knuth 1997, pp. 380–384
- ^ Knuth 1997, pp. 339–364
- ^ Reynaud, A.-A.-L. (1811). Traité d'arithmétique à l'usage des élèves qui se destinent à l'École Polytechnique (6th ed.). Paris: Courcier. Note 60, p. 34. As cited by Shallit (1994).
- ^ Finck, P.-J.-E. (1841). Traité élémentaire d'arithmétique à l'usage des candidats aux écoles spéciales (in الفرنسية). Derivaux.
- ^ أ ب Shallit 1994.
- ^ Lamé, G. (1844). "Note sur la limite du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers". Comptes Rendus de l'Académie des Sciences (in الفرنسية). 19: 867–870.
- ^ Grossman, H. (1924). "On the Number of Divisions in Finding a G.C.D". The American Mathematical Monthly. 31 (9): 443. doi:10.2307/2298146. JSTOR 2298146.
- ^ Honsberger, R. (1976). Mathematical Gems II. The Mathematical Association of America. pp. 54–57. ISBN 0-88385-302-7.
- ^ أ ب Knuth 1997, pp. 257–261
- ^ أ ب ت Crandall & Pomerance 2001, pp. 77–79, 81–85, 425–431
- ^ أ ب Möller, N. (2008). "On Schönhage's algorithm and subquadratic integer gcd computation" (PDF). Mathematics of Computation. 77 (261): 589–607. Bibcode:2008MaCom..77..589M. doi:10.1090/S0025-5718-07-02017-0.
- ^ أ ب ت Knuth 1997, p. 344
- ^ Ore 1948, p. 45
- ^ أ ب Knuth 1997, p. 343
- ^ Mollin 2008, p. 21
- ^ LeVeque 1996, p. 35
- ^ Mollin 2008, pp. 21–22
- ^ Knuth 1997, p. 353
- ^ Knuth 1997, p. 357
- ^ Tonkov, T. (1974). "On the average length of finite continued fractions". Acta Arithmetica. 26 (1): 47–57. doi:10.4064/aa-26-1-47-57.
- ^ Knuth, Donald E. (1976). "Evaluation of Porter's constant". Computers & Mathematics with Applications. 2 (2): 137–139. doi:10.1016/0898-1221(76)90025-0.
- ^ Porter, J. W. (1975). "On a Theorem of Heilbronn". Mathematika. 22 (1): 20–28. doi:10.1112/S0025579300004459.
- ^ Knuth, D. E. (1976). "Evaluation of Porter's Constant". Computers and Mathematics with Applications. 2 (2): 137–139. doi:10.1016/0898-1221(76)90025-0.
- ^ Dixon, J. D. (1970). "The Number of Steps in the Euclidean Algorithm". J. Number Theory. 2 (4): 414–422. Bibcode:1970JNT.....2..414D. doi:10.1016/0022-314X(70)90044-2.
- ^ Heilbronn, H. A. (1969). "On the Average Length of a Class of Finite Continued Fractions". In Paul Turán (ed.). Number Theory and Analysis. New York: Plenum. pp. 87–96. LCCN 76016027.
- ^ Knuth 1997, p. 354
- ^ أ ب Norton, G. H. (1990). "On the Asymptotic Analysis of the Euclidean Algorithm". Journal of Symbolic Computation. 10 (1): 53–58. doi:10.1016/S0747-7171(08)80036-3.
- ^ Knuth 1997, p. 355
- ^ Knuth 1997, p. 356
- ^ Knuth 1997, p. 352
- ^ Wagon, S. (1999). Mathematica in Action. New York: Springer-Verlag. pp. 335–336. ISBN 0-387-98252-3.
- ^ Cohen 1993, p. 14
- ^ Cohen 1993, pp. 14–15, 17–18
- ^
Sorenson, Jonathan P. (2004). "An analysis of the generalized binary GCD algorithm". High primes and misdemeanours: lectures in honour of the 60th birthday of Hugh Cowie Williams. Fields Institute Communications. Vol. 41. Providence, RI: American Mathematical Society. pp. 327–340. ISBN 9780821887592. MR 2076257.
The algorithms that are used the most in practice today [for computing greatest common divisors] are probably the binary algorithm and Euclid's algorithm for smaller numbers, and either Lehmer's algorithm or Lebealean's version of the k-ary GCD algorithm for larger numbers.
- ^ Knuth 1997, pp. 321–323
- ^ Stein, J. (1967). "Computational problems associated with Racah algebra". Journal of Computational Physics. 1 (3): 397–405. Bibcode:1967JCoPh...1..397S. doi:10.1016/0021-9991(67)90047-2.
- ^ Knuth 1997, p. 328
- ^ Lehmer, D. H. (1938). "Euclid's Algorithm for Large Numbers". The American Mathematical Monthly. 45 (4): 227–233. doi:10.2307/2302607. JSTOR 2302607.
- ^ Sorenson, J. (1994). "Two fast GCD algorithms". J. Algorithms. 16 (1): 110–144. doi:10.1006/jagm.1994.1006.
- ^ Weber, K. (1995). "The accelerated GCD algorithm". ACM Trans. Math. Softw. 21 (1): 111–122. doi:10.1145/200979.201042. S2CID 14934919.
- ^ Aho, A.; Hopcroft, J.; Ullman, J. (1974). The Design and Analysis of Computer Algorithms. New York: Addison–Wesley. pp. 300–310. ISBN 0-201-00029-6.
- ^ Schönhage, A. (1971). "Schnelle Berechnung von Kettenbruchentwicklungen". Acta Informatica (in الألمانية). 1 (2): 139–144. doi:10.1007/BF00289520. S2CID 34561609.
- ^ Cesari, G. (1998). "Parallel implementation of Schönhage's integer GCD algorithm". In G. Buhler (ed.). Algorithmic Number Theory: Proc. ANTS-III, Portland, OR. Lecture Notes in Computer Science. Vol. 1423. New York: Springer-Verlag. pp. 64–76.
- ^ Stehlé, D.; Zimmermann, P. (2005). "Gal's accurate tables method revisited". Proceedings of the 17th IEEE Symposium on Computer Arithmetic (ARITH-17). Los Alamitos, CA: IEEE Computer Society Press.
- ^ أ ب ت Lang, S. (1984). Algebra (2nd ed.). Menlo Park, CA: Addison–Wesley. pp. 190–194. ISBN 0-201-05487-6.
- ^ أ ب Weinberger, P. (1973). "On Euclidean rings of algebraic integers". Proc. Sympos. Pure Math. Proceedings of Symposia in Pure Mathematics. Providence, Rhode Island. 24: 321–332. doi:10.1090/pspum/024/0337902. ISBN 9780821814246.
- ^ أ ب ت Stillwell 2003, pp. 151–152
- ^ Boyer, C. B.; Merzbach, U. C. (1991). A History of Mathematics (2nd ed.). New York: Wiley. pp. 116–117. ISBN 0-471-54397-7.
- ^ Cajori, F (1894). A History of Mathematics. New York: Macmillan. p. 70. Reprinted, Dover Publications, 2004, ISBN 0-486-43874-0
- ^ Joux, Antoine (2009). Algorithmic Cryptanalysis. CRC Press. p. 33. ISBN 9781420070033.
- ^ Fuks, D. B.; Tabachnikov, Serge (2007). Mathematical Omnibus: Thirty Lectures on Classic Mathematics. American Mathematical Society. p. 13. ISBN 9780821843161.
- ^ Darling, David (2004). "Khintchine's constant". The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes. John Wiley & Sons. p. 175. ISBN 9780471667001.
- ^ Williams, Colin P. (2010). Explorations in Quantum Computing. Springer. pp. 277–278. ISBN 9781846288876.
- ^ Cox, Little & O'Shea 1997, pp. 37–46
- ^ Schroeder 2005, pp. 254–259
- ^ Grattan-Guinness, Ivor (1990). Convolutions in French Mathematics, 1800-1840: From the Calculus and Mechanics to Mathematical Analysis and Mathematical Physics. Volume II: The Turns. Science Networks: Historical Studies. Vol. 3. Basel, Boston, Berlin: Birkhäuser. p. 1148. ISBN 9783764322380.
Our subject here is the 'Sturm sequence' of functions defined from a function and its derivative by means of Euclid's algorithm, in order to calculate the number of real roots of a polynomial within a given interval
- ^ Hairer, Ernst; Nørsett, Syvert P.; Wanner, Gerhard (1993). "The Routh–Hurwitz Criterion". Solving Ordinary Differential Equations I: Nonstiff Problems. Springer Series in Computational Mathematics. Vol. 8 (2nd ed.). Springer. pp. 81ff. ISBN 9783540566700.
- ^ أ ب ت Stillwell 2003, pp. 101–116
- ^ أ ب ت Hensley, Doug (2006). Continued Fractions. World Scientific. p. 26. ISBN 9789812564771.
- ^ Dedekind, Richard (1996). Theory of Algebraic Integers. Cambridge Mathematical Library. Cambridge University Press. pp. 22–24. ISBN 9780521565189.
- ^ Johnston, Bernard L.; Richman, Fred (1997). Numbers and Symmetry: An Introduction to Algebra. CRC Press. p. 44. ISBN 9780849303012.
- ^ Adams, William W.; Goldstein, Larry Joel (1976). Introduction to Number Theory. Prentice-Hall. Exercise 24, p. 205. ISBN 9780134912820.
State and prove an analogue of the Chinese remainder theorem for the Gaussian integers.
- ^ Stark 1978, p. 290
- ^ Cohn 1980, pp. 104–105
- ^ Lauritzen, Niels (2003). Concrete Abstract Algebra: From Numbers to Gröbner Bases. Cambridge University Press. p. 130. ISBN 9780521534109.
- ^ Lauritzen (2003), p. 132
- ^ Lauritzen (2003), p. 161
- ^ أ ب Sharpe, David (1987). Rings and Factorization. Cambridge University Press. p. 55. ISBN 9780521337182.
- ^ Sharpe (1987), p. 52
- ^ Lauritzen (2003), p. 131
- ^ Lamé, G. (1847). "Mémoire sur la résolution, en nombres complexes, de l'équation An + Bn + Cn = 0". J. Math. Pures Appl. (in الفرنسية). 12: 172–184.
- ^ Edwards, H. (2000). Fermat's last theorem: a genetic introduction to algebraic number theory. Springer. p. 76.
- ^ Cohn 1980, pp. 104–110
- ^ LeVeque, W. J. (2002) [1956]. Topics in Number Theory, Volumes I and II. New York: Dover Publications. pp. II:57, 81. ISBN 978-0-486-42539-9. Zbl 1009.11001.
- ^ أ ب Clark, D. A. (1994). "A quadratic field which is Euclidean but not norm-Euclidean". Manuscripta Mathematica. 83 (1): 327–330. doi:10.1007/BF02567617. S2CID 895185. Zbl 0817.11047.
- ^ أ ب ت Bueso, Gómez-Torrecillas & Verschoren (2003); see pp. 37-38 for non-commutative extensions of the Euclidean algorithm and Corollary 4.35, p. 40, for more examples of noncommutative rings to which they apply.
- ^ أ ب Davidoff, Giuliana; Sarnak, Peter; Valette, Alain (2003). "2.6 The Arithmetic of Integer Quaternions". Elementary Number Theory, Group Theory and Ramanujan Graphs. London Mathematical Society Student Texts. Vol. 55. Cambridge University Press. pp. 59–70. ISBN 9780521531436.
- ^ Ribenboim, Paulo (2001). Classical Theory of Algebraic Numbers. Universitext. Springer-Verlag. p. 104. ISBN 9780387950709.













































































![{\displaystyle {\frac {a}{b}}=q_{0}+{\cfrac {1}{q_{1}+{\cfrac {1}{q_{2}+{\cfrac {1}{\ddots +{\cfrac {1}{q_{N}}}}}}}}}=[q_{0};q_{1},q_{2},\ldots ,q_{N}]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd6202ce1dc46510c7894abba456c3b899c58bf)
![{\displaystyle {\frac {1071}{462}}=2+{\cfrac {1}{3+{\cfrac {1}{7}}}}=[2;3,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41bb1b741861a853bc9f7bcbcd91315b07ffdac0)





















