مبرهنة طاليس

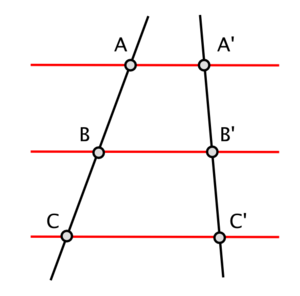
مبرهنة طاليس في الهندسة تقول أنه إذا قطع مستقيمان 3 مستقيمات متوازية فإننا نحصل على:

${\frac {A'B'}{AB}}={\frac {B'C'}{BC}}={\frac {A'C'}{AC}}$

---

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الصياغة

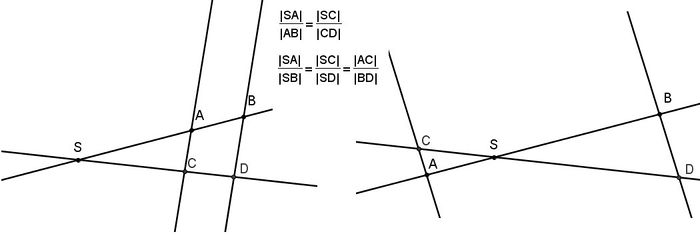
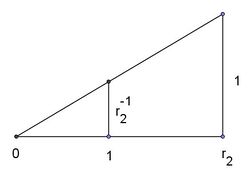
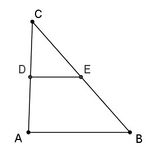
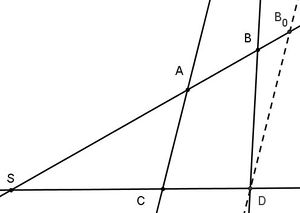
S is the point the intersection of 2 lines and A,B are the intersections of the first line with the 2 parallels, such that B is further away from S than A, and similarly are C, D the intersections of the second line with the 2 parallels such that D is further away from S than C.

1. The ratios of the any 2 segments on the first line equals the rations of the according segments on the second line: $|SA|:|AB|=|SC|:|CD|$, $|SB|:|AB|=|SD|:|CD|$, $|SA|:|SB|=|SC|:|SD|$
2. The ratio of the 2 segments on the same line starting at S equals the ratio of the segments on the parallels: $|SA|:|SB|=|SC|:|SD|=|AC|:|BD|$
3. The converse of the first statement is true as well, i.e. if the 2 intersecting lines are intercepted by 2 arbitrary lines and $|SA|:|AB|=|SC|:|CD|$ holds then the 2 intercepting lines are parallel. However the converse of the second statement is not true.
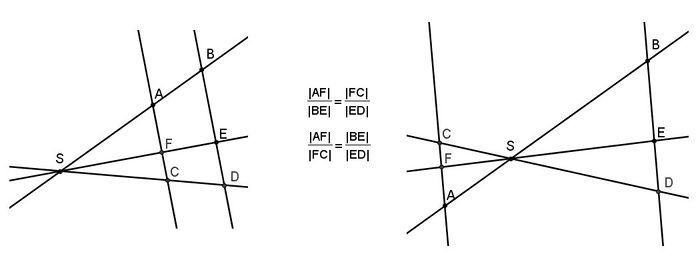
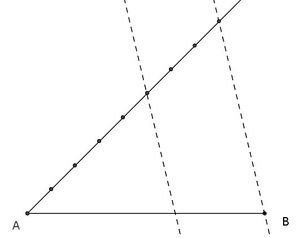
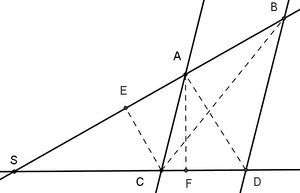
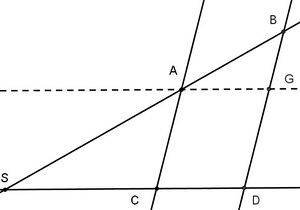
4. If you have more than 2 lines intersecting in S, then ratio of the 2 segments on a parallel equals the ratio of the according segments on the other parallel. An example for the case of 3 lines is given the second graphic below.

 التطبيقات

 الصياغة الجبرية لمنشآت الفرجار والمسطرة

There are 3 famous problems in elementary geometry, which were posed by the Greek in terms of Compass and straightedge constructions.

1. Trisecting the angle
2. Doubling the cube
3. Squaring the circle

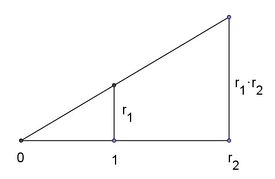
Their solution took more than 2000 years until all 3 of them finally were settled in the 19th century using algebraic methods that had become available during that period of time. In order to reformulate them in algebraic terms using field extensions, one needs to match field operations with compass and straightedge constructions. In particular it is important to assure that for 2 given line segments, a new line segment can be constructed such that its length equals the product of lengths of the other 2. Similarly one needs to be able to construct, for a line segment of length $d$, a new line segment of length $d^{-1}$. The intercept theorem can be used to show that in both cases the construction is possible.

Construction of a product

Construction of an Inverse

 تقسيم خط مستقيم بنسبة معينة

To divide an arbitrary line segment ${\overline {AB}}$ in a $m:n$ ratio you draw an arbitrary angle in A with ${\overline {AB}}$ as one leg. One other leg you construct $m+n$ equidistant points, then you draw line through the last point and B and parallel line through the mth point. This parallel line divides ${\overline {AB}}$ in the desired ratio. The graphic to the right shows the partition of a line sgement ${\overline {AB}}$ in a $5:3$ ratio.

 القياس/المساحة

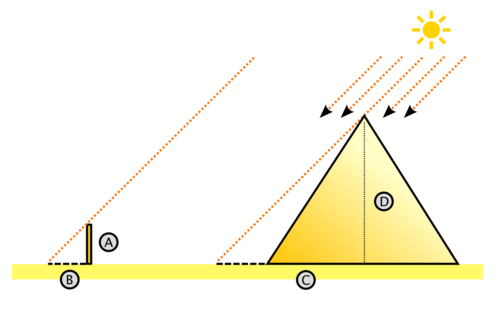
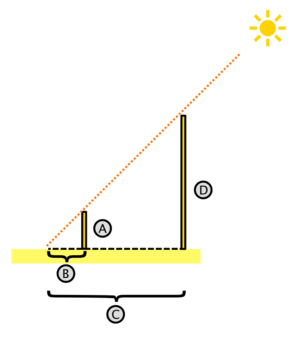
 Height of the Cheops Pyramid

According to some historical sources the Greek mathematician Thales applied the intercept theorem to determine the height of the cheops pyramid. He measured the shadow of a pole (B) with 2m, its height (A) with 1.63m, the shadow of the cheops pyramid with 63m, its base length with 230m. From that he computed $C=2m+63m+{\frac {230m}{2}}=180m$. Knowing A,B and C he was now able to apply the intercept theorem to compute $D={\frac {C\cdot A}{B}}={\frac {1.63m\cdot 180m}{2m}}=146.7m$

 قياس عرض النهر

The intercept theorem can be used determine a distance that cannot be measured directly, such as the width of a river or a lake, tall buildings or similar. The graphic to right illustrates the measuring of the width of a river. The segments $|CF|$,$|CA|$,$|FE|$ are measured and used to compute the wanted distance $|AB|={\frac {|AC||FE|}{|FC|}}$.

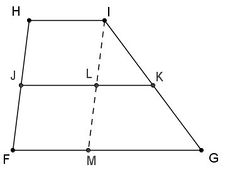
 Parallel Lines in Triangles and Trapezoids

The intercept theorem can be used to prove that a certain construction yields a parallel line (segment).

If the midpoints of 2 triangle sides are connected then the resulting line segment is parallel to the 3rd triangle side.

If the midpoints of 2 the non parallel sides of a trapezoid are connected, then the result line segment is parallel to the other 2 sides of the trapezoid.

 Proof

 claim 1

Due to heights of equal length ($CA\parallel BD$ ) we have $|\triangle CDA|=|\triangle CBA|$ and therefore $|\triangle SCB|=|\triangle SDA|$. This yields ${\frac {|\triangle SCA|}{|\triangle CDA|}}={\frac {|\triangle SCA|}{|\triangle CBA|}}$ and ${\frac {|\triangle SCA|}{|\triangle SDA|}}={\frac {|\triangle SCA|}{|\triangle SCB|}}$ Plugging in the actual formula for triangle areas (${\frac {baseline\cdot height}{2}}$) transforms that into ${\frac {|SC||AF|}{|CD||AF|}}={\frac {|SA||EC|}{|AB||EC|}}$ and ${\frac {|SC||AF|}{|SD||AF|}}={\frac {|SA||EC|}{|SB||EC|}}$ Cancelling the common factors results in: (a) $\,{\frac {|SC|}{|CD|}}={\frac {|SA|}{|AB|}}$ and (b) $\,{\frac {|SC|}{|SD|}}={\frac {|SA|}{|SB|}}$ Now use (b) to replace $|SA|$ and $|SC|$ in (a): ${\frac {\frac {|SA||SD|}{|SB|}}{|CD|}}={\frac {\frac {|SB||SC|}{|SD|}}{|AB|}}$ Using (b) again this simplifies to: (c) $\,{\frac {|SD|}{|CD|}}={\frac {|SB|}{|AB|}}$ $\,\square$

 claim 2

Draw an additional parallel to $SD$ through A. This parallel intersects $BD$ in G. Then you have $|AC|=|DG|$ and due to claim 1 ${\frac {|SA|}{|SB|}}={\frac {|DG|}{|BD|}}$ and therefore ${\frac {|SA|}{|SB|}}={\frac {|AC|}{|BD|}}$ $\square$

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 claim 3

Assume $AC$ and $BD$ are not parallel. Then the parallel line to $AC$ through $D$ intersects $SA$ in $B_{0}\neq B$. Since $|SB|:|SA|=|SD|:|SC|$ is true, we have $|SB|={\frac {|SD||SA|}{|SC|}}$ and on the other hand from claim 2 we have $|SB_{0}|={\frac {|SD||SA|}{|SC|}}$. So $B$ and $B_{0}$ are on the same side of $S$ and have the same distance to $S$, which means $B=B_{0}$. This is a contradiction, so the assumption could not have been true, which means $AC$ and $BD$ are indeed parallel $\square$

 claim 4

Can be shown by applying the intercept theorem for 2 lines.

 طالع أيضاً

• التماثل
• طاليس

 وصلات خارجية

• http://www.mathsrevision.net/gcse/pages.php?page=28
  
• http://kilian.ifastnet.com/applets_co/intercept_theorem/intercept_theorem.html
  
• http://www-history.mcs.st-and.ac.uk/Biographies/Thales.html