نقطة لاگرانج
النقاط اللاگرانجية (إنگليزية: Lagrangian points؛ /[invalid input: 'icon']ləˈɡrɑːndʒiən/؛ وأيضاً نقاط لاگرانج Lagrange points، النقاط-ل L-points، أو نقاط الميسان libration) هي خمس مواقع في نسق مداري حيث لا يؤثر على غرض صغير سوى الجاذبية ويمكن نظرياً أن يكون جزءاً من نمط ثابت الشكل مع جرمين أكبر (مثل ساتل مع الأرض والقمر). وتميز نقاط لاگرانج المواقع التي يعطي الشد المجمـّع للجاذبية من كتلتين كبيرتين بالضبط قوة الجذب المركزية المطلوبة لكي يدور معهما.
النقاط اللاگرانجية هي حلول أنماط ثابتة لمشكلة الأجرام الثلاثة المحدودة. فعلى سبيل المثال، إذا كان هناك جرمين هائلين في مدارين حول مركز كتلتيهما، فإن هناك خمس مواضع في الفراغ حيث يمكن وضع جرَم ثالث، بكتلة ضئيلة لدرجة يمكن تجاهلها نسبياً، وفي تلك النقاط يحتفظ الجرم الثالث بموقعه بالنسبة للجرمين الكبيرين. وكما يـُرى في إطار مرجعي دوراني يناظر السرعة الزاويّة لجرمين يدوران حول نفس المركز، فإن المجالين الثقاليين للجرمين الهائلين، مجتمعين مع تسارع الساتل، هم في اتزان فقط في "نقاط لاگرانج"، مما يتيح لجرم ثالث أن يكون ثابتاً نسبياً بالنسبة للجرمين الكبيرين.[1]
تاريخ ومفاهيم
نقاط لاگرانج الثلاثة الواقعين على خط مستقيم (L1, L2, L3) اكتشفهم ليونارد اويلر قبل بضع سنوات من اكتشاف لاگرانج للنقطتين الأخيرتين.[2][3]
في 1772، كان عالم الرياضيات الإيطالي-الفرنسي جوزيف لوي لاگرانج يعمل على مشكلة الأجرام الثلاثة الشهيرة عندما اكتشف شذوذ مثير للاهتمام في النتائج. ففي الأصل، كان هدفه اكتشاف طريقة ليحسب بسهولة التفاعل التثاقلي بين عدد عشوائي من الأجرام في نظام، لأن الميكانيكا النيوتنية تستنتج أن مثل هذا النظام ينتج عنه أن تدور الأجرام بشكل فوضوي حتى يحدث اصطدام، أو أن جرماً به خارج النظام حتى يمكن تحقيق اتزان.
The logic behind this conclusion is that a system with one body is trivial, as it is merely static relative to itself; a system with two bodies is the relatively simple two-body problem, with the bodies orbiting around their common center of mass. However, once more than two bodies are introduced, the mathematical calculations become very complicated. It becomes necessary to calculate the gravitational interaction between every pair of objects at every point along their trajectory.
Lagrange, however, wanted to make this simpler. He did so with a simple hypothesis: The trajectory of an object is determined by finding a path that minimizes the action over time. This is found by subtracting the potential energy from the kinetic energy. With this way of thinking, Lagrange re-formulated the classical Newtonian mechanics to give rise to Lagrangian mechanics.
Common opinion has been that Lagrange himself considered how a third body of negligible mass would orbit around two larger bodies which were already in a near-circular orbit, and found that in a frame of reference that rotates with the larger bodies, there are five specific fixed points where the third body experiences zero net force as it follows the circular orbit of its host bodies (planets). However, that is false.[4]
Actually, Lagrange considered in the first chapter of the Essai the general three-body problem. From that, in the second chapter, he demonstrated two special constant-pattern solutions, the collinear and the equilateral, for any three masses, with conic section orbits.[5] Thence, if one mass is made negligible, one immediately gets the five positions now known as the Lagrange Points; but Lagrange himself apparently did not note that.
Early in the 20th century, Trojan asteroids were discovered at the ل4 and ل5 Lagrange points of the Sun–Jupiter system.
In the more general case of elliptical orbits, there are no longer stationary points in the same sense: it becomes more of a Lagrangian “area”. The Lagrangian points constructed at each point in time, as in the circular case, form stationary elliptical orbits which are similar to the orbits of the massive bodies. This is due to Newton's second law (Force = Mass times Acceleration, or ), where p = mv (p the momentum, m the mass, and v the velocity) is invariant if force and position are scaled by the same factor. A body at a Lagrangian point orbits with the same period as the two massive bodies in the circular case, implying that it has the same ratio of gravitational force to radial distance as they do. This fact is independent of the circularity of the orbits, and it implies that the elliptical orbits traced by the Lagrangian points are solutions of the equation of motion of the third body.[بحاجة لمصدر]
النقاط اللاگرانجية
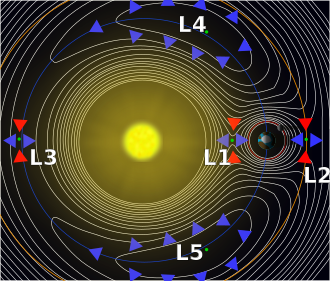
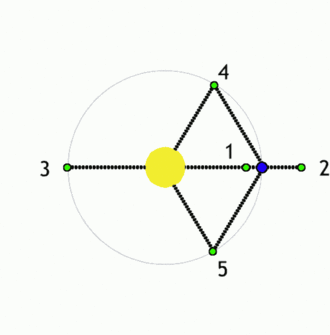
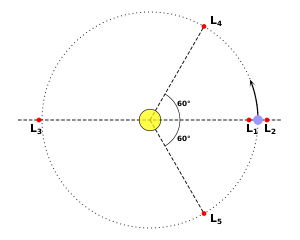
The five Lagrangian points are labeled and defined as follows:
ل1
The ل1 point lies on the line defined by the two large masses M1 and M2, and between them. It is the most intuitively understood of the Lagrangian points: the one where the gravitational attraction of M2 partially cancels M1 gravitational attraction.
- Example: An object which orbits the Sun more closely than the Earth would normally have a shorter orbital period than the Earth, but that ignores the effect of the Earth's own gravitational pull. If the object is directly between the Earth and the Sun, then the Earth's gravity weakens the force pulling the object towards the Sun, and therefore increases the orbital period of the object. The closer to Earth the object is, the greater this effect is. At the ل1 point, the orbital period of the object becomes exactly equal to the Earth's orbital period. ل1 is about 1.5 million kilometers from the Earth.[6]
ل2
The ل2 point lies on the line defined by the two large masses, beyond the smaller of the two. Here, the gravitational forces of the two large masses balance the centrifugal effect on a body at ل2.
- Example: On the side of the Earth away from the Sun, the orbital period of an object would normally be greater than that of the Earth. The extra pull of the Earth's gravity decreases the orbital period of the object, and at the ل2 point that orbital period becomes equal to the Earth's.
If the mass of the smaller object (M2) is much smaller than the mass of the larger object (M1) then ل1 and ل2 are at approximately equal distances r from the smaller object, equal to the radius of the Hill sphere, given by:
where R is the distance between the two bodies.
This distance can be described as being such that the orbital period, corresponding to a circular orbit with this distance as radius around M2 in the absence of M1, is that of M2 around M1, divided by :
أمثلة
- Sun and Earth: 1،500،000 km (930،000 mi) from the Earth
- Earth and Moon: 60،000 km (37،000 mi) from the Moon[7]
ل3
The ل3 point lies on the line defined by the two large masses, beyond the larger of the two.
- Example: ل3 in the Sun–Earth system exists on the opposite side of the Sun, a little outside the Earth's orbit but slightly closer to the Sun than the Earth is. (This apparent contradiction is because the Sun is also affected by the Earth's gravity, and so orbits around the two bodies' barycenter, which is, however, well inside the body of the Sun.) At the ل3 point, the combined pull of the Earth and Sun again causes the object to orbit with the same period as the Earth.
ل4 و ل5
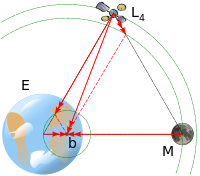
النقطتان ل4 و ل5 يقعان في الركنين الثالثين للمثلثين متساويي الأضلاع في مستوى المدار whose common base is the line between the centers of the two masses, such that the point lies behind (ل5) or ahead of (ل4) the smaller mass with regard to its orbit around the larger mass.
The reason these points are in balance is that, at ل4 and ل5, the distances to the two masses are equal. Accordingly, the gravitational forces from the two massive bodies are in the same ratio as the masses of the two bodies, and so the resultant force acts through the barycenter of the system; additionally, the geometry of the triangle ensures that the resultant acceleration is to the distance from the barycenter in the same ratio as for the two massive bodies. The barycenter being both the center of mass and center of rotation of the three-body system, this resultant force is exactly that required to keep the smaller body at the Lagrange point in orbital equilibrium with the other two larger bodies of the system (indeed, the third body need to have negligible mass). The general triangular configuration was discovered by Lagrange working on the three-body problem.
التسارع الشعاعي
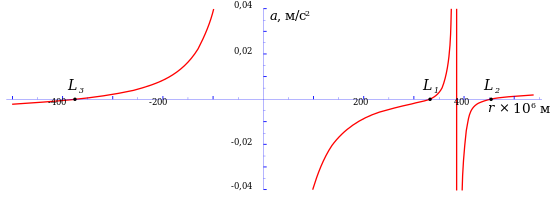
The radial acceleration a of an object in orbit at a point along the line passing through both bodies is given by:
where r is the distance from the large body M1, R is the distance between the two main objects and sgn(x) is the sign function of x. The terms in this function represent respectively: force from M1; force from M2; and centripetal force. The points L3, L1, L2 occur where the acceleration is zero — see chart at right. Positive acceleration is acceleration towards the right of the chart and negative acceleration is towards the left; that is why acceleration has opposite signs on opposite sides of the gravity wells.
الرحلات إلى النقاط اللاگرانجية
The Lagrangian point orbits have unique characteristics that have made them a good choice for performing some kinds of missions. These missions generally orbit the points rather than occupy them directly.
الرحلات السابقة والحالية
| الرحلة | النقطة اللاگرانجية | الوكالة | الوضع |
|---|---|---|---|
| Advanced Composition Explorer (ACE) | Sun–Earth ل1 | NASA | Operational[8] |
| Solar and Heliospheric Observatory (SOHO) | Sun–Earth ل1 | ESA, NASA | Operational[9] |
| WIND | Sun–Earth ل1 | NASA | Operational[10] |
| International Sun–Earth Explorer 3 (ISEE-3) | Sun–Earth ل1 | NASA | Original mission ended, left ل1 point[11] |
| Wilkinson Microwave Anisotropy Probe (WMAP) | Sun–Earth ل2 | NASA | Operational[12], graveyard orbit |
| Herschel and Planck Space Observatories | Sun–Earth ل2 | ESA | Operational [13][14] |
| Chang'e 2 | Sun–Earth ل2 | CNSA | Original mission ended, left ل2 point for 4179 Toutatis at April 15, 2012 [15] |
| ARTEMIS mission extension of THEMIS | Earth–Moon ل1 and ل2 | NASA | Operational [16] |
| GRAIL | Sun–Earth ل1 | NASA | Passed ل1, arrived at the Moon[17] |
المهام المستقبلية والمقترحة
| المهمة | النقطة اللاگرانجية | الوكالة | الوضع |
|---|---|---|---|
| Deep Space Climate Observatory | Sun–Earth ل1 | NASA | On hold[بحاجة لمصدر] |
| LISA Pathfinder (LPF) | Sun–Earth ل1 | ESA, NASA | Launch Date 2014 [18] |
| Solar-C | Sun–Earth ل1 | Japan Aerospace Exploration Agency | Possible mission after 2010[بحاجة لمصدر] |
| Gaia | Sun–Earth ل2 | ESA | Planned for August 2013 [19] |
| James Webb Space Telescope | Sun–Earth ل2 | NASA, ESA, Canadian Space Agency | Working on 2018 launch[20][21] |
| Euclid | Sun–Earth ل2 | ESA | Proposed for launch in 2019[22] |
| Wide Field Infrared Survey Telescope | Sun–Earth ل2 | NASA, U.S. Department of Energy | Proposed for launch in 2020[23] |
| "Lunar Far-Side Communication Satellites" | Earth–Moon ل2 | NASA | Proposed in 1968[24] |
| Exploration Gateway Platform | Earth–Moon ل2[25] | NASA | Proposed in 2011[26] |
| Space colonization and manufacturing | Earth–Moon ل4 or ل5 | L5 Society | Proposed in 1974[بحاجة لمصدر] |
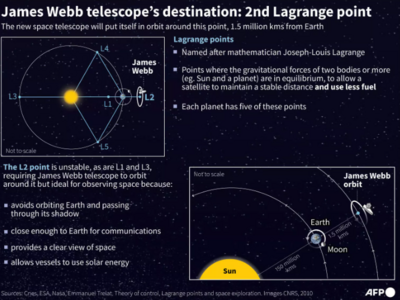
تلسكوپ جيمس وب الفضائي يصل إلى وجهته على بعد مليون ميل من الأرض
في 24 يناير 2022، أطلق تلسكوپ جيمس وب الفضائي دفعاته ووصل إلى وجهته المدارية على بعد حوالي 1.5 مليون كيلومتر من الأرض، بحسب ما أعلنته وكالة ناسا، وهو ما يمثل علامة فارقة في مهمته لدراسة التاريخ الكوني.[27]
أطلق التلسكوپ، الذي يُعتبر خليفة هابل، محركات الدفع الخاصة به على متنه لمدة خمس دقائق تقريباً كجزء من تصحيح المسار الأخير قبل الالتفاف حول نقطة لاگرانج الثانية من الشمس والأرض، أو النقطة L2، وفقاً لمدونة ناسا. نقاط لاگرانج هي مواضع في الفضاء تميل فيها الأجسام إلى البقاء، مع قوة الجاذبية لكتلتين كبيرتين تعادل قوة الجاذبية المركزية اللازمة للتحرك معها.
سيسمح مدار تلسكوپ جيمس وب برؤية واسعة للكون في أي لحظة، بالإضافة إلى فرصة أن تصبح بصريات التلسكوپ والأدوات العلمية باردة بدرجة كافية لتعمل بأداء علمي أمثل الآن بعد أن نُشرت مقاطع المرآة الأساسية والمرآة الثانوية في وب من مواقع الإطلاق، سيبدأ المهندسون العملية المعقدة التي تستغرق ثلاثة أشهر لمحاذاة بصريات التلسكوب بدقة تقارب النانومتر.[28]
وقد صرح بل نلسون-مسؤول عن الإدارة الوطنية للملاحة الجوية والفضاء:
| "تهانينا للفريق على كل عملهم الشاق لضمان وصول وب بأمان إلى L2 اليوم". "لقد اقتربنا خطوة واحدة من كشف أسرار الكون. ولا أطيق الانتظار لرؤية مناظر وب الأولى الجديدة للكون هذا الصيف!" |
وفقاً لوكالة ناسا، فإن موقع وب يمنحها رؤية واسعة للفضاء في أي وقت، وستكون درجات الحرارة باردة بدرجة كافية حتى "تعمل وتؤدي العلوم المثلى". كما قال مدير مشروع وب بل أوكس:
أُطلق التسلكوپ، نتيجة تعاون بين وكالة الفضاء الأوروپية ووكالة الفضاء الكندية، في 25 ديسمبر 2021، وطوال رحلته، قام بتوسيع مرآته إلى وضع مناسب للعمل.[29]
على الرغم من أنه كان من المتوقع في الأصل أن يمتد عمر وب من 5 إلى 10 سنوات، إلا أن وكالة ناسا قالت في بيان بعد الإطلاق أن الوقود الزائد سيسمح لها على الأرجح بالعمل "بشكل ملحوظ" لمدة تزيد عن 10 سنوات. حيث اختير مكان التلسكوپ الجديد نظراً لموقعه بين قوى الجاذبية من الشمس والأرض، مما يخلق توازناً يسمح لتلسكوب جيمس وب بالحفاظ على مداره بأقل قدر من الوقود.[30]
طالع أيضاً
- Euler's three-body problem
- List of objects at Lagrangian points
- Lunar space elevator
- Home on Lagrange (The L5 Song)
- جمعية ل5
- Horseshoe orbit
- Hill sphere
- Lagrange point colonization
- Lissajous orbit
- Lagrangian mechanics
- Gegenschein
- Co-orbital configuration
ملاحظات
الهامش
- ^ "نقاط لاگرانج" by Enrique Zeleny, مشروع إثباتات ولفرام.
- ^ Koon, W. S. (2006). Dynamical Systems, the Three-Body Problem, and Space Mission Design. p. 9.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) (16MB) - ^ Leonhard Euler, De motu rectilineo trium corporum se mutuo attrahentium (1765)
- ^ (بالفرنسية) Lagrange, Joseph-Louis (1867–92). "Tome 6, Chapitre II: Essai sur le problème des trois corps". Oeuvres de Lagrange. Gauthier-Villars. pp. 229–334.
- ^ (بالفرنسية) Lagrange, Joseph-Louis (1867–92). "Tome 6, Chapitre II: Essai sur le problème des trois corps". Oeuvres de Lagrange. Gauthier-Villars. pp. 229–334.
- ^ Cornish, Neil J. "The Lagrangian Points" (PDF). Montana State University - Department of Physics. Retrieved 29 July 2011.
{{cite web}}: Cite has empty unknown parameter:|coauthors=(help) - ^ Zegler, Frank; Bernard Kutter (2010-09-02). "Evolving to a Depot-Based Space Transportation Architecture". AIAA SPACE 2010 Conference & Exposition. AIAA. p. 4. Retrieved 2011-08-30. "We can create an energy savings account by moving propellant to the earth-moon Lagrange points - especially L2. Located 60,000 km beyond the moon, propellant or cargo cached at L2 is very nearly at earth escape energy. It takes only a small nudge to dislodge it from Earth's gravitational grasp. This has been known for decades and L2 is often called a gateway to the solar system."
- ^ "ACE Mission". Caltech ACE Science Center. Retrieved 2010-07-03.
- ^ "SOHO's Orbit: An Uninterrupted View of the Sun". NASA. Retrieved 2010-09-28.
- ^ "WIND Spacecraft". NASA. Retrieved 2010-09-28.
- ^ "Solar System Exploration: ISEE-3/ICE". NASA. Retrieved 2010-09-28.
- ^ "WMAP Facts". NASA. Retrieved 2010-06-27.
- ^ "Herschel Factsheet". European Space Agency. 17 April 2009. Retrieved 2009-05-12.
- ^ "Esa, latest news". European Space Agency. November 3, 2003. Retrieved July 5, 2009.
- ^ "嫦娥二号再接新任务预计年底飞掠小行星". 现代快报. Retrieved 2012-06-27.
- ^ "THEMIS". Space Sciences Laboratory, University of California, Berkeley. 9 September 2010. Retrieved 2010-09-10.
- ^ "GRAIL". NASA. Retrieved 2011-09-16.
{{cite web}}: Text "Gravity Recovery and Interior Laboratory" ignored (help) - ^ "LPF Mission". ESA. Retrieved 2012-07-09.
- ^ "Gaia overview". European Space Agency. Retrieved 2012-05-12.
- ^ "The James Webb Space Telescope: About JWST". NASA. Retrieved 2011-07-28.
- ^ "The James Webb Space Telescope Frequently Asked Questions: Webb's Orbit". NASA. Retrieved 2010-09-27.
- ^ "ESA Science & Technology: Euclid". ESA. Retrieved 2012-05-16.
- ^ "New Worlds, New Horizons in Astronomy and Astrophysics". Committee for a Decadal Survey of Astronomy and Astrophysics; National Research Council. Retrieved 2010-09-27. p. 12, p. 153.
- ^ P. E. Schmid (June 1968). "Lunar Far-Side Communication Satellites" (PDF). NASA. Retrieved 2008-07-16.
- ^ NASA teams evaluating ISS-built Exploration Platform roadmap]
- ^ Chris Bergin (December 2011). "Exploration Gateway Platform hosting Reusable Lunar Lander proposed". NASA Spaceflight.com. Retrieved 2011-12-05.
- ^ فرانس 24 (2022-01-24). "Webb telescope reaches destination, 1 mn miles from Earth: NASA". www.france24.com.
{{cite web}}: CS1 maint: numeric names: authors list (link) - ^ Alise Fisher (2022-01-24). "Orbital Insertion Burn a Success, Webb Arrives at L2". blogs.nasa.gov.
- ^ ياهوو نيوز (2022-01-24). "James Webb telescope reaches final destination a million miles from Earth". news.yahoo.com.
- ^ فوربس (2022-01-24). "1 Million Miles Away: NASA'S $10 Billon Webb Telescope Arrives". www.forbes.com.
وصلات خارجية
- Joseph-Louis, Comte Lagrange, from Oeuvres Tome 6, "Essai sur le Problème des Trois Corps" - Essai (PDF); source Tome 6 (Viewer)
- "Essay on the Three-Body Problem" by J-L Lagrange, translated from the above, in http://www.merlyn.demon.co.uk/essai-3c.htm.
- De motu rectilineo trium corporum se mutuo attrahentium - Leonhard Euler - PDF 227kB - very rough translation at http://www.merlyn.demon.co.uk/essai-3c.htm.
- What are Lagrange points? — European Space Agency page, with good animations
- Explanation of Lagrange points – Prof. Neil J. Cornish
- A NASA explanation – also attributed to Neil J. Cornish
- Explanation of Lagrange points – Prof. John Baez
- Geometry and calculations of Lagrange points – Dr J R Stockton
- Locations of Lagrange points, with approximations – Dr. David Peter Stern
- An online calculator to compute the precise positions of the 5 Lagrange points for any 2-body system – Tony Dunn
- Astronomy cast — Ep. 76: Lagrange Points Fraser Cain and Dr. Pamela Gay
- The Five Points of Lagrange by Neil deGrasse Tyson
- Earth, a lone Trojan discovered
- CS1 errors: unsupported parameter
- CS1: abbreviated year range
- CS1 errors: unrecognized parameter
- CS1 maint: numeric names: authors list
- Articles with hatnote templates targeting a nonexistent page
- Articles with redirect hatnotes needing review
- Articles containing إنگليزية-language text
- Pages using Lang-xx templates
- Ill-formatted IPAc-en transclusions
- Articles with unsourced statements from May 2010
- Articles with unsourced statements from September 2010
- طرواديون (فلك)


![{\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1175643479ba922598c78a6d4dfcf7fff160bfe7)