مماس
المماس أو خط الظل[1] أو الخط المُماسّ[2]Tangent، لأي منحنى عند نقطة عليه هو المستقيم الذي يقطع أو يشترك مع المنحنى في تلك النقطة
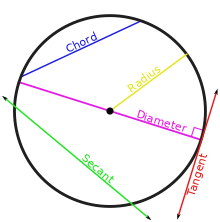
فالمستقيم مثلا إما أن يقطع الدائرة في نقطتين أو يمسها أو لا يقطعها (أي خارجيا عنها)
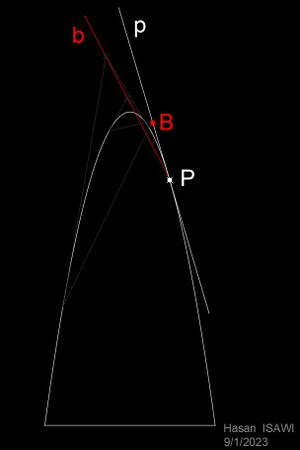
يمكن إعطاء عدة تعاريف بديهية لمستقيم ماس لمنحنى في نفس المستوى. أول فكرة هي في اعتبار المماس في نقطة P لمنحنى γ، أفضل خط مستقيم يُقرب المنحنى γ عند P.
في مجال الهندسة الاقليدية يمكن تعريف بشكل دقيق خط التماس لمنحنيات محددة. فإن مماس دائرة نصف قطرها r، ومركز O في نقطة P، على سبيل المثال، يمكن تعريفة كخط يمر في P، على مسافة r عن O، أو الخط الوحيد في المستوى الذي يشترك مع الدائرة في النقطة P. في نطاق الهندسة الفراغية، بطريقة مماثلة يمكن تحديد المستوى المماس لسطح. لتحديد المماس في حالة منحنى عام يُستخدم التفاضل (Calculus). مفهوم التماس هي واحد من أكثر المفاهيم الأساسية في الهندسة التفاضلية وجرى تعميمه على نطاق واسع، انظر فضاء التماس.
التاريخ
في الهندسة الوصفية
الفكرة البديهية لخط المماس للمنحنى هي فكرة الخط الذي "يلامس" المنحنى دون قطعه (تخيل المنحنى كما لو كان كيانا ماديًا لا يمكن اختراقه). الخط المستقيم الذي يقطع المنحنى يسمى قاطع.
علاوة على ذلك ، بالنظر إلى القاطع الذي يمر عبر نقطتين P و Q لمنحنى، يمكن اعتبار المماس عند P على أنه الخط المستقيم الذي يمر بالنقطة Q عندما تتطابق مع P.
هناك طريقة أخرى لرؤية مفهوم التماس من خلال التفكير في أن المماس عند نقطة P من منحنى γ هو الخط المستقيم الذي يشابه γ بالقرب من P.
حتى من هذه التعريفات غير الرسمية ، ندرك أنه قد تكون هناك حالات لا يتم فيها تعريف الخط المماس. على سبيل المثال ، إذا كان المنحنى ثلاثي وكان P رأسًا ، فلا يتوافق أي من التعريفين السابقين بشكل دقيق مع خط المماس المار بالنقطة P.
في الهندسة التركيبية، يمكن إعطاء تعريفات بديلة صارمة لخطوط مماس لمنحنيات محددة.[3] على سبيل المثال ، يمكن تعريف الخط المتماس لدائرة دلتا مركزها O ونصف قطرها r عند نقطة P (تنتمي لمحيط دلتا) على أنه الخط الذي يمر عبر P على مسافة r من O، أو على أنه الخط الوحيد بالمستوى الذي يتشارك مع الدائرة النقطة P.[4]
في الهندسة متعددة الأبعاد ، يمكن تحديد المستوى المتماس لسطح بطريقة مماثلة (فضاء مماس).
لتحديد التماس في حالة المنحنى العام ، يتم استخدام أدوات حساب التفاضل والتكامل متناهية الصغر بشكل عام.
خط التماس للمنحنى
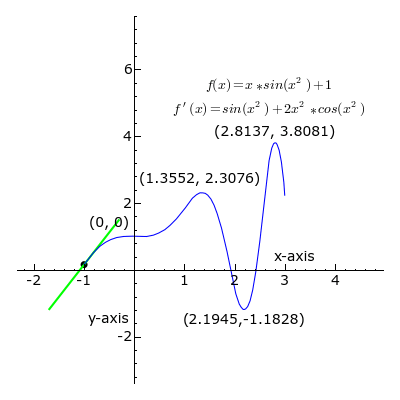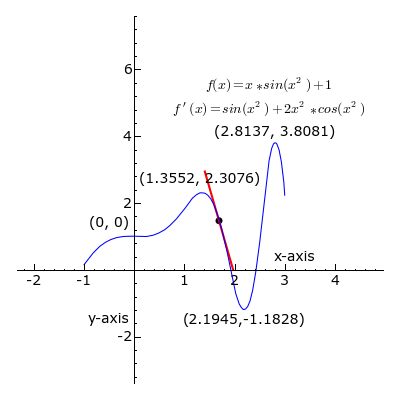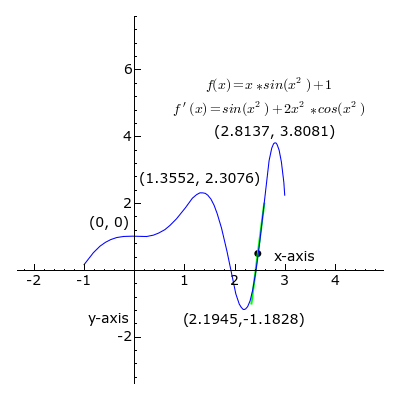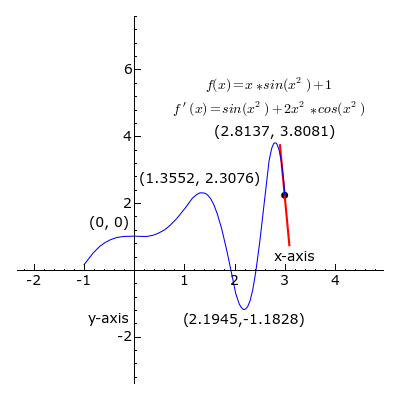
الطريقة التحليلية
المعادلات
الخط الناظم للمنحنى
الزاوية بين المنحنيات
الممسات المتعددة عند الأصل
دوائر المماس
الأسطح والتشعبات الأعلى
معرض
- تحول مماسي.jpg
وصلات مماسية بين دويريات مستوية
- Comune-tre-cicliche-gen.jpg
تحديد أحد المخروطيتين (باللون الأصفر) التي يشاركها ثلاث دويريات عامة.[5] الدورية العامة هي التي تحيط مخروطيات غير متشابهة فيما بينها.
- Tangenza-parabola-iperbole.jpg
تماس بين قطع مكافئ وقطع زائد
المصادر
- ^ محمد علي التهانوي. موسوعة كشاف اصطلاحات الفنون والعلوم. تحقيق علي دحروج، نقل النص الفارسي إلى العربية عبد الله الخالدي، الترجمة الأجنبية جورج زيناتي. الجزء الثاني. ص. ۱۹۰۰
- ^ ترجمة لاتينية: līnea tangēns
- ^ The problem of tangency to three non-homothetic conics. Dr. Hasan ISAWI Archived 2023-02-15 at the Wayback Machine
- ^ The problem of tangency to three non-homothetic conics
- ^ Geometric Loci Archived 2022-02-14 at the Wayback Machine
- J. Edwards (1892). Differential Calculus. London: MacMillan and Co. pp. 143 ff.
انظر أيضاً
- طريقة نيوتن
- ناظم السطح
- دائرة التقبيل
- منحنى التقبيل
- تعامد
- Subtangent
- خط دعم
- Tangent cone
- زاوية التماس
- Tangential component
- خطوط ودوائر التماس
وصلات خارجية
- Hazewinkel, Michiel, ed. (2001), "Tangent line", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Eric W. Weisstein, Tangent Line at MathWorld.
- Tangent to a circle With interactive animation
- Tangent and first derivative — An interactive simulation
- The Tangent Parabola by John H. Mathews