فونون
الفونون هو عبارة عن حالة اهتزاز مكممة تحدث في الشبكات البلورية الصلبة، مثل شبكات الذرات في الأجسام الصلبة، مما يجعلها تلعب دورا كبيرا في فيزياء الجسم الصلب حيث تسهم في تحديد العديد من خواص الجسم الصلب مثل الناقلية الحرارية والناقلية الكهربائية. عمليا يمكن أن تعزى للفونونات طويلة الموجة ظاهرة نشوء الصوت ضمن الأجسام الصلبة، كما تقوم الفونونات بتشكيل الآلية الرئيسة لنقل الحرارة ضمن الأجسام التي تصنف كعازلة.
الفونونات إذن هي تعبير كمومي لحالة خاصة من الحركة الاهتزازية، تعرف بالميكانيك الكلاسيكي بالحالات النظامية، وفيها تقوم جميع أجزاء الشبكة البلورية بالاهتزاز بنفس التواتر.
الفونون: هو كمة الطاقة للموجة الميكانيكية، أي إنه أصغر طاقة يمكن تبادلها بين منبع صوتي ووسط مادي، وهو بهذا المعنى، نظير الفوتون في الأمواج الكهرمغنطيسية الذي يمثل أصغر طاقة كهرمغنطيسية تتبادلها موجة كهرمغنطيسية مع وسط مادي. وتعطى طاقة الفونون، على غرار الفوتون، بعلاقة من الشكل W=hν لا تعتمد إلا على تواتر المنبع الصوتي، وثابت التناسب h هو ثابت بلانك وقيمته: h=6.6×10-34 J.s[1]
ميكانيك الكم
يأتي المبرر النظري لمفهوم الفونون من تطبيق المعادلة الأساسية في ميكانيك الكم على انتشار الاهتزازات الجيبية في الأوساط المادية، إلا أن طبيعة الأمواج الصوتية تختلف عن الأمواج الكهرمغنطيسية اختلافاً بيِّناً، إذ إن الأمواج الصوتية تجعل الجسيمات المادية للوسط الذي تنتشر فيه تهتز اهتزازاً دورياً حول موضع وسطي ثابت، وهو ما تعاني منه ذرات المادة الصلبة في درجات الحرارة العادية. إن تآثر الذرات المتجاورة ينتقل تدريجياً بسرعة محددة v عبر المادة تمثل سرعة انتشار الموجة في الوسط المادي وهي تساوي 340 متراً في الثانية في حالة الهواء وتقارب عشرة أضعاف ذلك في الأوساط الصلبة.
تواتر الأمواج
يقع تواتر الأمواج الصوتية التي تتحسس بها آذاننا دون 20000 هرتز، فهي إذاً منخفضة نسبياً. إلا أنه بالطبع يمكن توليد أمواج فوق صوتية ultrasons تواترها أعلى بكثير قد يصل إلى 1010 هرتز، وذلك عن طريق إثارة بلورة كوارتز من النوع الكهرضغطي piézo-électrique بأمواج كهرمغنطيسية كأمواج الرادار، وهنا يتم الحديث عن أمواج يفوق تواترها تواتر الأمواج فوق الصوتية تسمى hyperons.
ولما كان للذرات عطالة بسبب كتلتها فهي لا تتأثر بالحركات السريعة جداً التي ترافق الأمواج الصوتية عالية التواتر. ومن هنا يدرك المرء اعتماد سرعة انتشار الموجة v على تواترها ν. وترتبط سرعة انتشار الموجة بطولها λ بالعلاقة:
ومنه نجد طويلة الشعاع الموجي:
ولذلك فإن الشعاع الموجي المرافق للفونون الذي يتجه باتجاه انتشار الموجة يتناسب طرداً وتواتر الموجة. وواقع الأمر أن الشعاع الموجي المرافق للفونون يرتبط بعلاقة أكثر تعقيداً ويتعلق بطبيعة الوسط الذي تنتشر فيه الموجة. وهي علاقة يطلق عليها اسم علاقة التبديد dispersion وتتغير بتغير الوسط.
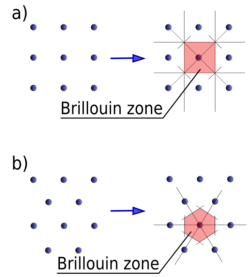
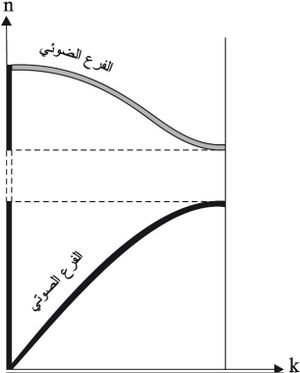
يمثل الشكل (1) علاقة التبديد العائدة لوسط مؤلف من نوعين من الذرات مختلفين في الكتلة، إذ يبدو جلياً خلو الشكل من بعض قيم ν. ويميّز في الشكل فرع يدعى فوع الفونونات الصوتية phonons acoustiques المقابل للتواترات المنخفضة، وفرع يدعى فرع الفونونات الضوئية phonons optiques المقابل للتواترات العالية، وقد سمي بذلك لمجاورته لتواترات الأمواج الضوئية.
يمكن النظر إلى الإثارة الحرارية السائدة في مادة صلبة على أنها ناشئة من تراكب عدد هائل من الأمواج الصوتية تنتشر في جميع الاتجاهات وتتوزع تواتراتها على جميع مجالات التواتر الممكنة. وباستخدام قوانين الإحصاء يمكن إيجاد عدد الفونونات عند كل تواتر nν. وهكذا فعل كل من آينشتاين Einstein وديباي Debye وبورن Born وكارمان Karman لدى عرضهم نظرية كمومية تتعلق بالحرارات النوعية للمواد chaleurs spécifiques. إنّ تخفيض درجة حرارة المادة تخفيضاً شديداً إلى درجة T قريبة من الصفر المطلق يزيد من عدد الفونونات التي تحمل طاقـة hν تفوق طاقتها طاقـة الإثارة الحرارية KT حـيث (K ثابت بولتزمان)، ولذا فقد شاعت دراسة خصائص الأجسام الصلبة في درجات الحرارة المنخفضة.
وعلى غـرار الأمواج الكهرمغنطيسية يمكن أن يعزى للأمواج الصوتية اندفاع p متناسب مع طاقتها w بحيث يكون:
. وبالإفادة من علاقة الطاقة يكون:
وبالتالي فإن اندفاع الفونون متناسب مع الشعاع الموجي k، تماماً كما هو شأن الفوتون. وهكذا يمكن النظر إلى علاقة التبديد بين تواتر الموجة ν وشعاع الموجة على أنها علاقة تربط بين طاقة الفونون واندفاعه، وعليه فإن تبادل طاقة الفونونات في الأمواج الصوتية يرافقه تغير في اندفاعها. وهذا بالضبط ما يخضع له الضوء لدى تبعثره على جسيمات مادية كالنترونات مثلاً، أو لدى تبعثر الأشعة السينية في المواد الصلبة، أو لدى دراسة تبعثر بريلوان Brillouin. ففي هذا النوع الأخير من التبعثر يمكن لفوتون من موجة ضوئية يجتاز وسطاً ما أن يمتص طاقة فونون واندفاعه متحولاً إلى فوتون ضوئي آخر، تختلف طاقته قليلاً عما كانت عليه وكذلك اندفاعه، وهو ما يحدث بالضبط لدى امتصاص الأشعة تحت الحمراء في المادة. وعليه فإن علاقة التبديد تضع قيوداً دقيقة وصارمة على تبادل الطاقة (أي على تغير طول الموجة) وعلى تغير الاندفاع.
وقد ساعد مفهوم الفونون من حيث إنه جسيم افتراضي يرافق انتشار الأمواج الصوتية على فهم كثير من خصائص المادة الصلبة، مثل تغير التوصيل الحراري للمادة والتوصيل الكهربائي لها بتغير درجة الحرارة. ومن هذا القبيل فقد تبين أن انتقال الحرارة في المواد العازلة يتم بفعل الفونونات، أما في المعادن جيدة التوصيل للحرارة فيتم بفضل الفونونات والإلكترونات معاً، ولذا فإن توصيلها الحراري يفوق سابقتها بعشرات المرات بل بالمئات.
ميكانيكا جسيمات في عـِقد
The potential energy of the entire lattice is the sum of all the pairwise potential energies:
where is the position of the th atom, and is the potential energy between two atoms.
طاقة الوضع للعقد يمكن كتابتها الآن كالتالي
Here, is the natural frequency of the harmonic potentials, which we assume to be the same since the lattice is regular. is the position coordinate of the th atom, which we now measure from its equilibrium position. The sum over nearest neighbors is denoted as "(nn)".
موجات عقدية
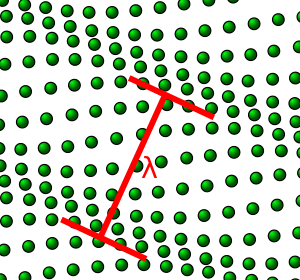
تشتت الفونونات في سلسلة أحادية البعد من ذرات متماثلة
Consider a one-dimensional quantum mechanical harmonic chain of N identical atoms. This is the simplest quantum mechanical model of a lattice, and we will see how phonons arise from it. The formalism that we will develop for this model is readily generalizable to two and three dimensions. The Hamiltonian for this system is
where is the mass of each atom, and and are the position and momentum operators for the th atom. A discussion of similar Hamiltonians may be found in the article on the quantum harmonic oscillator.
One can show that, for any two atoms and ,
which is exactly what we would expect for a lattice wave with frequency and wave number .
وفي ثلاثة أبعاد، تأخذ الهاملتونية الشكل التالي:
العزم البلوري
 مقالة مفصلة: العزم البلوري
مقالة مفصلة: العزم البلوري
حيث
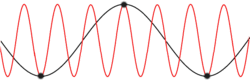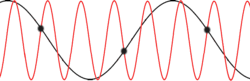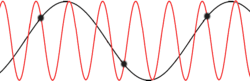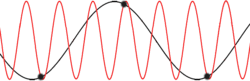
والجدير بالملاحظة أننا بحاجة إلى اعتبار مماثل في analog-to-digital conversion حيث يمكن حدوث aliasing في بعض الظروف.
الخواص الترموديناميكية
where is the frequency of the phonons (or photons) in the state, is Boltzmann's constant, and is the temperature.
انظر أيضاً
- Fracton
- مرونة خطية
- Rayleigh wave
- Surface acoustic wave
- Rigid Unit Modes a phonon where polyhedra move, by translation and/or rotation, without distorting
- Phononic crystal
- a vibron is for a molecule what a phonon is for a crystal
المصادر
- ^ أحمد حصري. "الفونون". الموسوعة العربية. Retrieved 2012-09-01.
وصلات خارجية
- PHONONS 2007: 12th International Conference on Phonon Scattering in Condensed Matter [1].

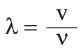
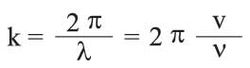














![{\displaystyle \langle k|x_{j}(t)x_{\ell }(0)|k\rangle ={\frac {\hbar }{Nm\omega _{k}}}\cos \left[k(j-\ell )a-\omega _{k}t\right]+\langle 0|x_{j}(t)x_{\ell }(0)|0\rangle }](https://www.marefa.org/api/rest_v1/media/math/render/svg/fe8a3c2beb786c78096256ab33e9f42a04322743)