ڤارنگ
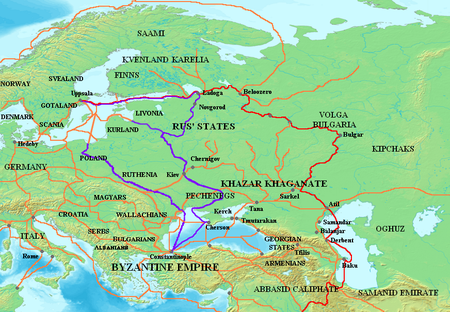
الڤارنگ (Varangians ؛ نورسية القديمة: Væringjar؛ Greek: Βάραγγοι Varangoi, Βαριάγοι Variagoi) was the name given by Greeks and East Slavs to Vikings,[1][2][3][4] who between the 9th and 11th centuries ruled the medieval state of Kievan Rus', settled among many rivers in territories of modern Ukraine, Belarus and Russia and formed the Byzantine Varangian Guard.[5][6] According to the 12th century Kievan Primary Chronicle, a group of Varangians known as the Rus'[7] settled in Novgorod in 862 under the leadership of Rurik. Before Rurik, the Rus' might have ruled an earlier hypothetical polity. Rurik's relative Oleg conquered Kiev in 882 and established the state of Kievan Rus', which was later ruled by Rurik's descendants.[8][9]
Engaging in trade, piracy, and mercenary activities, Varangians roamed the river systems and portages of Gardariki, as the areas north of the Black Sea were known in the Norse sagas. They controlled the Volga trade route (between the Varangians and the Arabs), connecting the Baltic to the Caspian Sea, and the Dnieper and Dniester trade route (between Varangians and the Greeks) leading to the Black Sea and Constantinople.[10] Those were the critically important trade links at that time, connecting Medieval Europe with wealthy and developed Arab Caliphates and the Byzantine Empire;[11] Most of the silver coinage in the West came from the East via those routes.
Attracted by the riches of Constantinople, the Varangian Rus' initiated a number of Rus'-Byzantine Wars, some of which resulted in advantageous trade treaties. At least from the early 10th century many Varangians served as mercenaries in the Byzantine Army, constituting the elite Varangian Guard (the personal bodyguards of Byzantine Emperors). Eventually most of them, both in Byzantium and in Eastern Europe, were converted from paganism to Orthodox Christianity, culminating in the Christianization of Kievan Rus' in 988. Coinciding with the general decline of the Viking Age, the influx of Scandinavians to Rus' stopped, and Varangians were gradually assimilated by East Slavs by the late 11th century.
أصل الاسم
Medieval Greek Βάραγγος Várangos and Old East Slavic Варягъ Varjagŭ (Old Church Slavonic Варѧгъ Varęgŭ) are derived from Old Norse væringi, originally a compound of vár 'pledge' or 'faith', and gengi 'companion', thus meaning 'sworn companion', 'confederate', extended to mean 'a foreigner who has taken service with a new lord by a treaty of fealty to him', or 'protégé'.[1][12] Some scholars seem to assume a derivation from vár with the common suffix -ing.[13] Yet, this suffix is inflected differently in Old Norse, and furthermore, the word is attested with -gangia and cognates in other Germanic languages in the Early Middle Ages, as in Old English wærgenga, Old Frankish wargengus and Langobardic waregang.[14] The reduction of the second part of the word could be parallel to that seen in Old Norse foringi 'leader', correspondent to Old English foregenga and Gothic 𐍆𐌰𐌿𐍂𐌰𐌲𐌰𐌲𐌲𐌾𐌰 fauragaggja 'steward'.[15][16]
روس الكييڤية

The terms “Varangian” and “Rus” can sometimes be used interchangeably but there are slight differences between the two groups. Both refer to the peoples of Scandinavian descent who settled in the Dnieper-Volga region during and after the 8th century. The Varangians are a more clearly definable group. They were Scandinavians in Eastern Europe who were often associated with Byzantium and the Byzantine emperor’s Varangian Guard. These mercenaries were almost entirely men who either returned to their Scandinavian homeland or married into the local Slavic culture. The term “Rus” is more difficult to define. The Rus were more inclined to settle in towns with their families. The term “Rus” is sometimes used in primary sources to describe Slavic peoples as well as Scandinavians. Its definition becomes clearer later in the period when it developed from the name of a people to the name of a political entity and area of land.[17] The confusion in the primary sources about the meaning of Rus' has led to arguments between scholars about whether Russia was named after a Scandinavian people or a Slavic people. These are grouped into Normanist and anti-Normanist views (with the broader meaning of Norman, i.e. 'Norse-men'). Current scholarship supports the Normanist argument – that the Rus were a primarily Scandinavian people – but there have been heated debates in the last century between certain scholars fueled by nationalism. It is now generally accepted that the Rus' were of Scandinavian origin but adopted Slavic cultural characteristics fairly quickly.[18]
Having settled Aldeigja (Ladoga) in the 750s, Scandinavian colonists played an important role in the early ethnogenesis of the Rus' people and in the formation of the Rus' Khaganate. The Varangians (Varyags in Old East Slavic) are first mentioned by the Primary Chronicle as having exacted tribute from the Slavic and Finnic tribes in 859. The Vikings were rapidly expanding in Northern Europe: England began to pay Danegeld (gold and other tribute to the Danish) in 859, and the Curonians of Grobin (in modern Latvia) faced an invasion by the Swedes around the same period. Due largely to geographic considerations, it is often argued that most of the Varangians who traveled and settled in the eastern Baltic, Russia, and lands to the south came from the area of modern Sweden.[19]
In the 9th century, the Rus' operated the Volga trade route, which connected Northern Russia (Gardariki) with the Middle East (Serkland). The Volga route declined by the end of the century, and the Dnieper and Dniester routes rapidly overtook it in popularity. Apart from Ladoga and Novgorod, Gnyozdovo and Gotland were major centres for Varangian trade.[20]

According to the Primary Chronicle, in 862, the Finnic and Slavic tribes in the area of Novgorod rebelled against their Varangian rulers, driving them overseas back to Scandinavia, but they soon started to conflict with each other. The disorder prompted the tribes to invite the Varangians back "to come and rule them" and bring peace to the region. Led by Rurik and his brothers Truvor and Sineus, the invited Varangians (called Rus') settled around the town of Holmgård (Novgorod). The Primary Chronicle twice names Rus' among the other Varangian peoples, including Swedes, Gutes, "Normans", and "Angles" (Normans was an Old Slavonic term for Norwegians not the Normans, while Angles may be interpreted as Danes, not Anglo-Saxons).[21] In some places, the chronicle mentions Slavs and Rus' as different groups, while in other instances it mixes them. In the study of the etymology of the word Rus' itself several possible origins are identified, but none are conclusive or very helpful in defining the Rus' people themselves.
The problem with confusion of names is most relevant to the earlier periods of Scandinavian colonization in the area. By the time the political entity of the Kievan Rus existed the Rus were considered to be a people of mixed Scandinavian/Slavic ethnicity but with a distinctly Slavic culture.
Under the leadership of Rurik's relative Oleg, the Varangian Rus' expanded southwards by capturing Kiev from the Khazars, founding the medieval state of Rus'.[8] Attracted by the riches of Constantinople and the Arab world, Varangians initiated a number of Rus'-Byzantine Wars, some of which resulted in advantageous trade treaties. Meanwhile, descendants of Rurik expanded the Rus' state and unified the local tribes. Contact with the Byzantine Empire increased, culminating in the Christianization of Kievan Rus' in 988، في عهد ڤلاديمير الأكبر.

As with the Norse influence in Normandy and the الجزر البريطانية, Varangian culture did not survive in the East. Instead, the Varangian ruling classes of the two powerful city-states of Novgorod and Kiev were gradually slavicised by the end of the 11th century.[22] However, the successor descendants of Rurik were the ruling dynasty of medieval Kievan Rus', the successor principalities of Galicia-Volhynia (after 1199), Chernigov, Vladimir-Suzdal, the Grand Duchy of Moscow, and the founders of the Tsardom of Russia.[23] The name of the Varangian Rus' became that of the land of Ruthenia and later modern Russia, and the ethnonym of its population.[24]
Many historians tend to agree with the Primary Chronicle that the Varangians organized the native settlements into the political entity of Kievan Rus' in the 880s and gave their name to the land. The Varangians were assimilated by East Slavs by the late 11th century. Historians minimize their role in the long-term development of the Kievan state because they left few traces of any permanent influence on Russia. Historian A.D. Stokes says:
- Few significant traces of Varangian influence can be discovered in Russian law, political institutions, social organizations, religious beliefs, language, or literature.[25]
العالم الإسلامي

The Rus' initially appeared in Serkland in the 9th century, traveling as merchants along the Volga trade route, selling furs, honey, and slaves, as well as luxury goods such as honey, amber, Frankish swords, and walrus ivory.[26] These goods were mostly exchanged for Arabic silver coins, called dirhams. Hoards of 9th century Baghdad-minted silver coins have been found in Sweden, particularly in Gotland. Variations in the size of the coin hoards show that there were phases of increased importation of coins and sometime decades during which very few coins were imported.[27]
The economic relationship between the Rus and the Islamic world developed quickly into a sprawling network of trading routes. Initially the Rus founded Staraya Ladoga as the first node from the Baltic to the Caspian Sea and Black Sea. By the end of the 9th century Staraya Ladoga was replaced as the most important center by Novgorod. From these centers the Rus were able to send their goods as far as Baghdad. Baghdad was the political and cultural center of the Islamic world in the 9th and 10th centuries and the Rus merchants who went there to trade their goods for silver interacted with cultures and goods from the Islamic World, but also from China, India, and North Africa.[28]
The trade between the Rus and the lands south of the Black and Caspian seas made it possible for cultural interactions to take place between the Rus and the Islamic World. The account written by Ibn Fadlan about his 921-922 travels from Baghdad to the capital of the Bulghar kingdom gives details which can reveal the cultural interaction between the two groups. Ibn Fadlan gives a vivid description of the daily habits of the Rus, as well as the only known first-person account of the complicated ship-burning funeral ceremony. Certain details in his account, especially the dialogue of the ceremonies and his personal conversations with Rus individuals, show that the Rus and the Arabs were interested in and fairly knowledgeable about each other’s cultures.[29]
The geography of the Volga region and the relative lack of physical wealth available for stealing (compared to targets of Viking raids in the west) made raiding a less important aspect of the Rus/Varangian activities in the East. Some raiding, however, was necessary to gain initial control of the towns and regions that they developed into centers of economic activities.[30] The first small-scale raids took place in the late 9th and early 10th centuries. The Rus' undertook the first large-scale expedition in 913; having arrived on 500 ships, they pillaged Gorgan, in the territory of present-day Iran, and the adjacent areas, taking slaves and goods. On their return, the northern raiders were attacked and defeated by Khazar Muslims in the Volga Delta, and those who escaped were killed by the local tribes on the middle Volga.
During their next expedition in 943, the Rus' captured Barda, the capital of Arran, in the modern-day Republic of Azerbaijan. The Rus' stayed there for several months, killing many inhabitants of the city and amassing substantial plunder. It was only an outbreak of dysentery among the Rus' that forced them to depart with their spoils. Sviatoslav, prince of Kiev, commanded the next attack, which destroyed the Khazar state in 965. Sviatoslav's campaign established Rus' control over the north-south trade routes, helping to alter the demographics of the region. Raids continued through the time period with the last Scandinavian attempt to reestablish the route to the Caspian Sea led by Ingvar the Far-Travelled in 1041.
الامبراطورية البيزنطية

The earliest Byzantine record of the Rus' may have been written prior to 842. It is preserved in the Greek Life of St. George of Amastris, which speaks of a raid that had extended into Paphlagonia. Contemporary Byzantine presence of the Rus' is mentioned in the Frankish Annals of St. Bertin. These relate that a delegation from the court of the Byzantine emperor visited Frankish Emperor Louis the Pious at his court in Ingelheim in 839. In this delegation were two men who called themselves Rhos (Rhos vocari dicebant). Louis enquired about their origins and learnt that they were Swedes. Fearing that they were spies for their brothers, the Danes, he incarcerated them.
In 860, the Rus' under Askold and Dir launched their first attack on Constantinople from Kiev. The result of this attack is disputed, but the Varangians continued their efforts as they regularly sailed on their monoxyla down the Dnieper into the Black Sea. The Rus' raids into the Caspian Sea were recorded by Arab authors in the 870s and in 910, 912, 913, 943, and later. Although the Rus' had predominantly peaceful trading relations with the Byzantines, the rulers of Kiev launched the relatively successful naval expedition of 907 and the abortive campaign of 941 against Constantinople, as well as the large-scale invasion of the Balkans by Sviatoslav I in 968–971. These raids were successful in forcing the Byzantines to re-arrange their trading arrangements; militarily, the Varangians were usually defeated by the superior Byzantine forces, especially in the sea due to Byzantine use of Greek fire.
الحرس الڤارنگي

The Varangian Guard (Greek: Τάγμα των Βαράγγων, Tágma tōn Varángōn) were a part of Byzantine Army and personal bodyguards of the Byzantine emperors from the 10th to the 14th centuries. Initially the guard was composed of Varangians who came from Kievan Rus'.
The guard was first formed under Emperor Basil II after 988, following the Christianization of Kievan Rus' and union with Vladimir I of Kiev, who sent 6,000 men to Basil as part of a military assistance agreement. Basil's distrust of the native Byzantine guardsmen, whose loyalties often shifted with fatal consequences, as well as the proven loyalty of the Varangians, many of whom served in Byzantium even before, led the emperor to employ them as his personal guard. Over the years, new recruits from Sweden, Denmark, and Norway kept a predominantly Scandinavian cast to the organization until the late 11th century. So many Scandinavians left to enlist in the guard that a medieval Swedish law from Västergötland stated that no one could inherit while staying in "Greece" — the then Scandinavian term for the Byzantine Empire.[32] In the eleventh century, there were also two other European courts that recruited Scandinavians:[33] Kievan Rus', c. 980–1060, and London, 1018–1066 (the Þingalið).[33]
Composed primarily of Scandinavians for the first hundred years, the guard increasingly included Anglo-Saxons after the successful Norman Conquest of England. By the time of Emperor Alexios Komnenos in the late 11th century, the Varangian Guard was largely recruited from Anglo-Saxons and "others who had suffered at the hands of the Vikings and their cousins the Normans". The Anglo-Saxons and other Germanic peoples shared with the Vikings a tradition of faithful, oath-bound service (to death if necessary), and after the Norman Conquest of England there were many fighting men, who had lost their lands and former masters, looking for a living elsewhere.
The Varangian Guard not only provided security for Byzantine emperors but participated in many wars involving Byzantium and often played a crucial role, since it was usually employed at critical moments of battle. By the late 13th century, Varangians were mostly ethnically assimilated by Byzantines, though the guard operated until at least the mid-14th century, and in 1400 there were still some people identifying themselves as "Varangians" in Constantinople.
في الثقافة الشعبية
- Rosemary Sutcliff's 1976 historical novel Blood Feud depicts Basil II's formation of the Varangian Guard from the point of view of a half-Saxon orphan who journeyed to Constantinople via the Dnieper trade route.
- Henry Treece's Viking Trilogy recounts the adventures of Harald Sigurdson, including service in the Varangian Guard.
- Michael Ennis's Byzantium ISBN 978-0-330-31596-8, a fictionalised version of the life of Harald Hardrada, features time in the Varangian Guard.
- In The Bulpington of Blup (1933) by H.G. Wells, the father of the protagonist maintains for years the fiction that he is at work on "a History of the Varangians that was to outshine Doughty".
- The John Ringo Paladin of Shadows series features a fictional, long-forgotten enclave of the Varangian Guard in the mountains of Georgia.
- Turisas' second studio album The Varangian Way is a concept album that tells the story of a group of Scandinavians travelling the river routes of medieval Russia, through Ladoga, Novgorod and Kiev to the Byzantine Empire. Their third album, Stand Up and Fight, describes the history of the Varangian Guard's service to the Byzantine Empire.
- Bearded axe-wielding Easterlings known as "Variags" appear in Tolkien's fantasy novel The Return of the King.
- In the PC game series Mount & Blade, the name and location of the Vaegirs echos the Varangians. Their faction have a unique unit called a "Vaegir Guard".
- In the video games Medieval: Total War and Medieval II: Total War the Varangian Guard is an axe-wielding elite infantry unit of the Byzantine Empire.
- Track 5 of Amon Amarth's seventh studio album Twilight of the Thunder God has the title "Varyags of Miklagaard".
- Track 2 of Grand Magus's eight studio album Sword Songs is titled "Varangian".
- Varangian soldiers are a common enemy in the video game Assassin's Creed: Revelations.
- Russian writer Dmitry Bykov's novel Living Souls (ЖД) involved a civil war between Varangians and Khazars over the control of Russia
- Varangians in Dark Souls II were pirates pressed into service of the King of Drangleic.
- In the Warhammer 40K universe, there is a chapter of space marines known as the "Space Wolves" that also go by the "Vaerangian Guard"
- In the PC game Crusader Kings 2[34] the Varangian Guard appear as a mercenary unit available exclusively to the Byzantine emperor.
- The Walking Drum by Louis L'Amour[مطلوب توضيح]
انظر أيضاً
- For the Scandinavians who travelled westward, see Vikings
- Byzantine army
- Byzantine bureaucracy and aristocracy
- Christianization of Kievan Rus'
- Komnenian army
- Kylfings
- Oeselians
- Piraeus Lion (inscription made by Varangians)
- Rulers of Kievan Rus'
الهامش
- ^ أ ب "Varangian," Online Etymology Dictionary
- ^ "Oleg". Encyclopædia Britannica. Retrieved 30 September 2015.
- ^ "Varangian". TheFreeDictionary.com. Retrieved 30 September 2015.
- ^ "væringer". Store norske leksikon. Retrieved 30 September 2015.
- ^ Milner-Gulland, R. R. Atlas of Russia and the Soviet Union. Phaidon. p. 36. ISBN 0-7148-2549-2.
- ^ Schultze, Sydney (2000). Culture and Customs of Russia. Greenwood Publishing Group. p. 5. ISBN 0-313-31101-3.
- ^ "Пушкинский Дом (ИРЛИ РАН) > Новости". Archived from the original on 16 March 2015. Retrieved 30 September 2015.
{{cite web}}: Unknown parameter|deadurl=ignored (|url-status=suggested) (help) - ^ أ ب Duczko, Wladyslaw (2004). Viking Rus. Brill Publishers. pp. 10–11. ISBN 90-04-13874-9. Retrieved 1 December 2009.
- ^ "Rurik Dynasty". Encyclopædia Britannica. Retrieved 30 September 2015.
- ^ Stephen Turnbull, The Walls of Constantinople, AD 324–1453, Osprey Publishing, ISBN 1-84176-759-X.
- ^ Schofield, Tracey Ann Vikings, Lorenz Educational Press, p. 7, ISBN 978-1-5731-0356-5
- ^ H.S. Falk & A. Torp, Norwegisch-Dänisches Etymologisches Wörterbuch, 1911, pp. 1403–4; J. de Vries, Altnordisches Etymologisches Wörterbuch, 1962, pp. 671–2; S. Blöndal & B. Benedikz, The Varangians of Byzantium, 1978, p. 4
- ^ Hellquist 1922:1096, 1172; M. Vasmer, Russisches etymologisches Wörterbuch, 1953, vol. 1, p. 171.
- ^ Blöndal & Benedikz, p. 4; D. Parducci, "Gli stranieri nell’alto medioevo", Mirator 1 (2007)in Italian, English abstract
- ^ Falk & Torp, p. 1403; other words with the same second part are: Old Norse erfingi 'heir', armingi or aumingi 'beggar", bandingi 'captive', hamingja 'luck', heiðingi 'wolf', lausingi or leysingi 'homeless'; cf. Falk & Torp, p. 34; Vries, p. 163.
- ^ Bugge, Sophus, Arkiv för nordisk filologi 2 (1885), p. 225
- ^ Andrushchuk, Fjodor (2008). "The Vikings in the East". In Price, Neil S.; Brink, Stefan (eds.). The Viking World. London: Routledge. p. 533.
- ^ Klejn, Leo S. (2013). "From Goths to Varangians: Communication and cultural exchange between the Baltic and the Black Sea". In Lind, John; Bjerg, Line Maj-Britt Hojberg; Sindbaek, Soren M. (eds.). The Russian Controversy over the Varangians. Aarhus: Aarhus University Press. p. 29.
- ^ Forte, Angelo; Oram, Richard; and Pedersen, Frederik. Viking Empires. Cambridge University Press, 2005 ISBN 0-521-82992-5. pp. 13–14.
- ^ A massive majority (40,000) of all Viking-Age Arabian coins found in Scandinavia were found in Gotland. In Skåne, Öland and Uppland together, about 12,000 coins were found. Other Scandinavian areas have only scattered finds: 1,000 from Denmark and some 500 from Norway. Byzantine coins have been found almost exclusively in Gotland, some 400.
See:
Burenhult, Göran (1999). Arkeologi i Norden 2 [Archeology in the Nordic countries, part 2] (in Swedish). Stockholm: Natur & Kultur. ISBN 9789127134782.{{cite book}}: CS1 maint: unrecognized language (link)
See also:
Gardell, Carl Johan (1987). Gotlands historia i fickformat [The pocket history of Gotland] (in Swedish). ISBN 91-7810-885-3.{{cite book}}: CS1 maint: unrecognized language (link) - ^ Duczko, Wladyslaw (2004). Viking Rus. BRILL. pp. 10–11. ISBN 90-04-13874-9.
- ^ Encyclopædia Britannica. "Viking". Retrieved 19 August 2011.
- ^ Encyclopædia Britannica. "Rurik dynasty". Retrieved 18 August 2011.
- ^ "Russia" Online Etymology Dictionary
- ^ A.D. Stokes, "Kievan Russia," in Robert Auty, and Dimitri Obolensky, eds. Companion to Russian Studies: vol 1: An Introduction to Russian History (1981) p 53.
- ^ Batey, Colleen E.; Graham-Campbell, James (1994). Cultural Atlas of the Viking World. New York: Facts on File. p. 194.
- ^ Batey, Colleen E.; Graham-Campbell, James (1994). Cultural Atlas of the Viking World. New York: Facts on File. p. 198.
- ^ Batey, Colleen E.; Graham-Campbell, James (1994). Cultural Atlas of the Viking World. New York: Facts on File. p. 184.
- ^ Montgomery, James E. (2000). "Ibn Fadlan and the Rusiyyah". Journal of Arabic and Islamic Studies. 3.
- ^ Noonan, Thomas S. (1997). "Scandinavians in Eastern Europe". In Sawyer, Peter S. (ed.). The Oxford Illustrated History of the Vikings. Oxford: Oxford University Press. p. 135.
- ^ Wortley, John, ed. (2010), John Skylitzes: A Synopsis of Byzantine History, 811–1057, Cambridge, United Kingdom: Cambridge University Press, p. 372, ISBN 978-0-521-76705-7, https://books.google.com/books?id=vGE8Xq832A0C
- ^ Jansson 1980:22
- ^ أ ب Pritsak 1981:386
- ^ "Mercenaries". Retrieved 30 September 2015.
للاستزادة
Primary sources
- Russian Primary Chronicle
- Strategikon of Kekaumenos by Kekaumenos
- Alexiad by Anna Komnena
- Deeds of John and Manuel Comnenus by John Kinnamos
- Historia ecclesiastica by Ordericus Vitalis
- Chronicon universale anonymi Laudunensis
- Játvarðar Saga
- Heimskringla
- Laxdœla saga
مصادر ثانوية اضافية
- Buckler, Georgina. Anna Comnena: A Study. Oxford: University Press, 1929.
- Blondal, Sigfus. Varangians of Byzantium: An Aspect of Byzantine Military History. Trans. by Benedikt S. Benedikz, Cambridge: 1978. ISBN 0-521-21745-8.
- Davidson, H.R. Ellis. The Viking Road to Byzantium. London: 1976. ISBN 0-04-940049-5.
- Enoksen, Lars Magnar. (1998). Runor: historia, tydning, tolkning. Historiska Media, Falun. ISBN 91-88930-32-7.
- Jansson, Sven B. (1980). Runstenar. STF, Stockholm. ISBN 91-7156-015-7.
- English Refugees in the Byzantine Armed Forces: The Varangian Guard and Anglo-Saxon Ethnic Consciousness by Nicholas C.J. Pappas for De Re Militari.org
- Raffaele D'Amato; Rava, Giuseppe (illustrator). The Varangian Guard 988-1453. "Men-at-Arms" series, Osprey, 2010. ISBN 978-1849081795. Illustrated reconstruction of arms and armor of Varangians.
قالب:Campaignbox Russo-Byzantine Wars قالب:Russo-Byzantine Treaties قالب:Gardariki
- CS1 errors: unsupported parameter
- Articles containing نورسية القديمة-language text
- Pages using Lang-xx templates
- Articles with hatnote templates targeting a nonexistent page
- جميع الصفحات التي تحتاج تنظيف
- مقالات بالمعرفة تحتاج توضيح from February 2017
- Pages using div col with unknown parameters
- ڤارنگ
- روس الكييڤية'
- قتال العصور الوسطى
- سكندناڤيا
- شعوب جرمانية