مدار الأرض

(تم التحويل من مدار حول الأرض)
يجب ألا يـُخلـَط بينها وبين Earth orbit.
Earth at seasonal points in its orbit (not to scale)
Earth orbit (yellow) compared to a circle (gray)

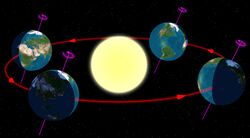
المدار الأرضي، هو حركة الأرض حول الشمس، at an average distance of 149.60 million km (92.96 million mi),[1] and one complete orbit takes 365.256 days (1 sidereal year), during which time Earth has traveled 940 million km (584 million mi).[2] Ignoring the influence of other solar system bodies, Earth's orbit is an ellipse with the Earth-Sun barycenter as one focus and a current eccentricity of 0.0167; since this value is close to zero, the center of the orbit is close, relative to the size of the orbit, to the center of the Sun.

As seen from Earth, the planet's orbital prograde motion makes the Sun appear to move with respect to other stars at a rate of about 1° eastward per solar day (or a Sun or Moon diameter every 12 hours).[nb 1] Earth's orbital speed averages 29.78 km/s (107,208 km/h; 66,616 mph), which is fast enough to cover the planet's diameter in 7 minutes and the distance to the Moon in 4 hours.[3]

From a vantage point above the north pole of either the Sun or Earth, Earth would appear to revolve in a counterclockwise direction around the Sun. From the same vantage point, both the Earth and the Sun would appear to rotate also in a counterclockwise direction about their respective axes.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

تاريخ الدراسة

المقالة الرئيسية: Heliocentrism
Heliocentric Solar System
Heliocentrism (lower panel) in comparison to the geocentric model (upper panel), not to scale

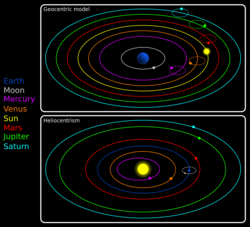
Heliocentrism is the scientific model that first placed the Sun at the center of the Solar System and put the planets, including Earth, in its orbit. Historically, heliocentrism is opposed to geocentrism, which placed the Earth at the center. Aristarchus of Samos already proposed a heliocentric model in the third century BC. In the sixteenth century, Nicolaus Copernicus' De revolutionibus presented a full discussion of a heliocentric model of the universe [4] in much the same way as Ptolemy had presented his geocentric model in the second century. This "Copernican revolution" resolved the issue of planetary retrograde motion by arguing that such motion was only perceived and apparent. "Although Copernicus's groundbreaking book... had been [printed more than] a century earlier, [the Dutch mapmaker] Joan Blaeu was the first mapmaker to incorporate his revolutionary heliocentric theory into a map of the world."[5]


التأثير على الأرض

المقالة الرئيسية: موسم

Because of Earth's axial tilt (often known as the obliquity of the ecliptic), the inclination of the Sun's trajectory in the sky (as seen by an observer on Earth's surface) varies over the course of the year. For an observer at a northern latitude, when the north pole is tilted toward the Sun the day lasts longer and the Sun appears higher in the sky. This results in warmer average temperatures, as additional solar radiation reaches the surface. When the north pole is tilted away from the Sun, the reverse is true and the weather is generally cooler. North of the Arctic Circle and south of the Antarctic Circle, an extreme case is reached in which there is no daylight at all for part of the year, and continuous daylight during the opposite time of year. This is called polar night and midnight sun, respectively. This variation in the weather (because of the direction of the Earth's axial tilt) results in the seasons.[6]

أحداث في المدار

The Hill sphere (gravitational sphere of influence) of the Earth is about 1,500,000 kilometers (0.01 AU) in radius, or approximately four times the average distance to the Moon.[7][nb 2] This is the maximal distance at which the Earth's gravitational influence is stronger than the more distant Sun and planets. Objects orbiting the Earth must be within this radius, otherwise, they may become unbound by the gravitational perturbation of the Sun.

Orbital characteristics
epoch J2000.0[nb 3]
aphelion 152.10×10^6 km (94.51×10^6 mi)
1.0167 AU[nb 4]
perihelion 147.10×10^6 km (91.40×10^6 mi)
0.98329 AU[nb 4]
semimajor axis 149.60×10^6 km (92.96×10^6 mi)
1.000001018 AU[8]
eccentricity 0.0167086[8]
inclination 7.155° to Sun's equator
1.578690°[9] to invariable plane
longitude of the ascending node 174.9°[8]
longitude of perihelion 102.9°[8]
argument of periapsis 288.1°[8][nb 5]
period 365.256363004 days[10]
average orbital speed 29.78 km/s (18.50 mi/s)[3]
107,208 km/h (66,616 mph)
speed at aphelion 29.29 km/s (18.20 mi/s)[3]
speed at perihelion 30.29 km/s (18.82 mi/s)[3]

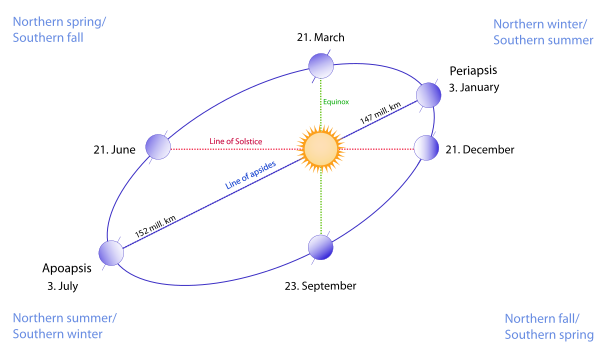
The following diagram shows the relation between the line of the solstice and the line of apsides of Earth's elliptical orbit. The orbital ellipse goes through each of the six Earth images, which are sequentially the perihelion (periapsis — nearest point to the Sun) on anywhere from January 2 to January 5, the point of March equinox on March 19, 20, or 21, the point of June solstice on June 20, 21, or 22, the aphelion (apoapsis — the farthest point from the Sun) on anywhere from July 3 to July 5, the September equinox on September 22, 23, or 24, and the December solstice on December 21, 22, or 23.[11] The diagram shows a very exaggerated shape of Earth's orbit; the actual orbit is virtually circular.

Seasons1.svg

Because of the axial tilt of the Earth in its orbit, the maximal intensity of Sun rays hits the Earth 23.4 degrees north of the equator at the June Solstice (at the Tropic of Cancer), and 23.4 degrees south of the equator at the December Solstice (at the Tropic of Capricorn).[12]

المستقبل

المقالة الرئيسية: إستقرار النظام الشمسي


انظر أيضاً

الهوامش

  1. ^ Our planet takes about 365 days to orbit the Sun. A full orbit has 360°. That fact demonstrates that each day, the Earth travels roughly 1° in its orbit. Thus, the Sun will appear to move across the sky relative to the stars by that same amount.
  2. ^ For the Earth, the Hill radius is
    where m is the mass of the Earth, a is an astronomical unit, and M is the mass of the Sun. So the radius in AU is about .[بحاجة لمصدر]
  3. ^ All astronomical quantities vary, both secularly and periodically. The quantities given are the values at the instant J2000.0 of the secular variation, ignoring all periodic variations.
  4. ^ أ ب aphelion = a × (1 + e); perihelion = a × (1 – e), where a is the semi-major axis and e is the eccentricity.
  5. ^ The reference lists the longitude of perihelion, which is the sum of the longitude of the ascending node and the argument of perihelion. That is, 114.20783° + (−11.26064°) = 102.94719°.
خطأ استشهاد: الوسم <ref> ذو الاسم "asc_node" المُعرّف في <references> غير مستخدم في النص السابق.

المصادر

  1. ^ "Sun: Facts & Figures". Solar System Exploration. National Aeronautics and Space Administration. Archived from the original on يوليو 3, 2015. Retrieved يوليو 29, 2015.
  2. ^ Jean Meeus, Astronomical Algorithms 2nd ed, ISBN 0-943396-61-1 (Richmond, VA: Willmann-Bell, 1998) 238. See Ellipse#Circumference. The formula by Ramanujan is accurate enough.
  3. ^ أ ب ت ث Williams, David R. (2004-09-01). "Earth Fact Sheet". NASA. Retrieved 2007-03-17.
  4. ^ De revolutionibus orbium coelestium. Johannes Petreius. 1543.
  5. ^ Jerry Brotton, A History of the World in Twelve Maps, London: Allen Lane, 2012, ISBN 9781846140990 p. 262.
  6. ^ "What causes the seasons? (NASA)". Retrieved January 22, 2015.
  7. ^ Vázquez, M.; Montañés Rodríguez, P.; Palle, E. (2006). "The Earth as an Object of Astrophysical Interest in the Search for Extrasolar Planets" (PDF). Instituto de Astrofísica de Canarias. Retrieved 2007-03-21.
  8. ^ أ ب ت ث ج خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة VSOP87
  9. ^ Allen, Clabon Walter; Cox, Arthur N. (2000). Allen's Astrophysical Quantities. Springer. p. 294. ISBN 0-387-98746-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
  10. ^ The figure appears in multiple references, and is derived from the VSOP87 elements from section 5.8.3, p. 675 of the following: Simon, J. L.; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. (February 1994). "Numerical expressions for precession formulae and mean elements for the Moon and planets". Astronomy and Astrophysics. 282 (2): 663–683. Bibcode:1994A&A...282..663S.
  11. ^ خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة :0
  12. ^ "What is the significance of the Tropic of Cancer, Tropic of Capricorn, Arctic Circle, and Antarctic Circle?". Retrieved January 22, 2015.

خطأ استشهاد: الوسم <ref> ذو الاسم "standish_williams_iau" المُعرّف في <references> غير مستخدم في النص السابق.

خطأ استشهاد: الوسم <ref> ذو الاسم "IERS" المُعرّف في <references> غير مستخدم في النص السابق.
تمّ الاسترجاع من "https://www.marefa.org/w/index.php?title=مدار_الأرض&oldid=2288275"