كرة
| Sphere | |
|---|---|
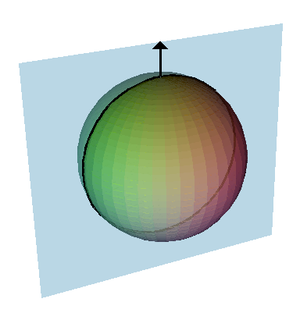
 إسقاط منظور ثنائي الأبعاد للكرة | |
| النوع | Smooth surface Algebraic surface |
| خاصية أويلر | 2 |
| Symmetry group | O(3) |
| المساحة السطحية | 4πr2 |
| الحجم | 4/3πr3 |
الكرة Sphere هي غرض هندسي في فراغ ثلاثي الأبعاد أي سطح كرة (بمعنى ، مماثل للدائرة في الفضاء ثنائي الأبعاد. شكلياً، فإن الكرة هي مجموعة من النقاط التي تكون كلها على نفس المسافة r من نقطة معينة نقطة ، ولكن في مساحة ثلاثية الأبعاد.[1] هذه المسافة r هي نصف القطر للكرة ، والتي تتكون من جميع النقاط بمسافة أقل من (أو ، بالنسبة للكرة المغلقة ، أقل من أو يساوي إلى) r من نقطة معينة ، وهي مركز للكرة الرياضياتية. ويشار إليها أيضًا باسم نصف قطر الكرة ومركزها ، على التوالي. أطول جزء من الخط المستقيم عبر الكرة ، يربط بين نقطتين من الكرة ، يمر عبر المركز وبالتالي يكون طوله ضعف نصف القطر ؛ إنه قطر لكل من المجسم الكروي والكرة.
The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings.
بينما خارج الرياضيات ، يتم استخدام المصطلحين "المجسم الكروي" و "الكرة" في بعض الأحيان بالتبادل ، في الرياضيات يتم التمييز أعلاه بين "المجسم الكروي" ، وهو ثنائي الأبعاد سطح مغلق المضمّن في الفضاء الإقليدي ثلاثي الأبعاد و "الكرة" ، وهو شكل ثلاثي الأبعاد يتضمن الكرة وكل شيء "داخل" الكرة ("كرة مغلقة") ، أو ، في كثير من الأحيان ، مجرد نقاط "داخل" ، ولكن "ليس على" الكرة ("كرة مفتوحة"). لم يتم دائمًا الحفاظ على التمييز بين "الكرة" و "المجسم الكروي" وخاصة المراجع الرياضية القديمة التي تتحدث عن المجال على أنه صلب. هذا مشابه للحالة في المستوى ، حيث يمكن أيضًا الخلط بين مصطلحي "دائرة" و "قرص".
المصطلحات الأساسية
As mentioned earlier r is the sphere's radius; any line from the center to a point on the sphere is also called a radius.[2]
If a radius is extended through the center to the opposite side of the sphere, it creates a diameter. Like the radius, the length of a diameter is also called the diameter, and denoted d. Diameters are the longest line segments that can be drawn between two points on the sphere: their length is twice the radius, d = 2r. Two points on the sphere connected by a diameter are antipodal points of each other.[2]
A unit sphere is a sphere with unit radius (r = 1). For convenience, spheres are often taken to have their center at the origin of the coordinate system, and spheres in this article have their center at the origin unless a center is mentioned.
A great circle on the sphere has the same center and radius as the sphere, and divides it into two equal hemispheres.
Although the figure of Earth is not perfectly spherical, terms borrowed from geography are convenient to apply to the sphere. A particular line passing through its center defines an axis (as in Earth's axis of rotation). The sphere-axis intersection defines two antipodal poles (north pole and south pole). The great circle equidistant to the poles is called the equator. Great circles through the poles are called lines of longitude or meridians. Small circles on the sphere that are parallel to the equator are circles of latitude (or parallels). In geometry unrelated to astronomical bodies, geocentric terminology should be used only for illustration and noted as such, unless there is no chance of misunderstanding.[2]
Mathematicians consider a sphere to be a two-dimensional closed surface embedded in three-dimensional Euclidean space. They draw a distinction between a sphere and a ball, which is a three-dimensional manifold with boundary that includes the volume contained by the sphere. An open ball excludes the sphere itself, while a closed ball includes the sphere: a closed ball is the union of the open ball and the sphere, and a sphere is the boundary of a (closed or open) ball. The distinction between ball and sphere has not always been maintained and especially older mathematical references talk about a sphere as a solid. The distinction between "circle" and "disk" in the plane is similar.
Small spheres or balls are sometimes called spherules, e.g. in Martian spherules.
المعادلات
في الهندسة التحليلية ، كرة ذات مركز (x0, y0, z0) ونصف القطر r هو موضع لجميع النقاط (x, y, z) مثل ذلك
لنجعل a, b, c, d, e أرقام حقيقية مع a ≠ 0 ولكن
فتكون المعادلة
لا يوجد نقاط حقيقية كحل إذا ويسمى معادلة مجسم كروي تخيلي. If , الحل الوحيد ل هو النقطة المعادلة تسمى لتكون معادلة نقطة مجسم كروي. أخيراً, في حالة , هي معادلة المجسم الكروي الذي مركزه والذي نصف قطره .[1]
إذا a في المعادلة أعلاه هي صفر ثم f(x, y, z) = 0 هي معادلة المستوى. وهكذا ، يمكن اعتبار المستوى ككرة نصف قطر لانهائي يكون مركزها نقطة عند اللانهاية.[3]
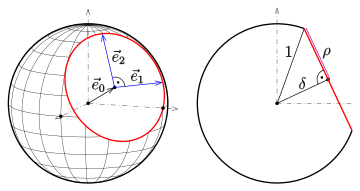
النقاط على الكرة مع نصف القطر و المركز يمكن أن تكون پارامتراً عبر
الپارامتر يمكن أن تترافق مع الزاوية المحسوبة موجبة من اتجاه المحور الموجب "z" - من خلال المركز إلى متجه نصف القطر ، و الپارامتر يمكن أن تترافق مع الزاوية المحسوبة موجبة من اتجاه المحور "x" الموجب - من خلال المركز إلى إسقاط متجه نصف القطر على المستوى xy"" -.
كرة أي نصف قطر تتمركز عند الصفر هي سطح متكامل من الشكل التفاضلي التالي:
تعكس هذه المعادلة متجهات الموضع والسرعة للنقطة, (x, y, z) and (dx, dy, dz), الانتقال على الكرة دائمًا متعامد مع بعضهم البعض.
يمكن أيضًا إنشاء كرة كسطح يتكون عن طريق تدوير دائرة حول أي من الأقطار. بما أن الدائرة هي نوع خاص من القطع الناقص ، فإن الكرة هي نوع خاص من دوران القطع الناقص. باستبدال الدائرة بقطع ناقص يدور حول محوره الرئيسي ، يصبح الشكل متطاولاً كروياً ؛ كروي مفلطح يدور حول المحور الثانوي.[5]
الخصائص
حجم مغلق
في ثلاثة أبعاد ، الحجم داخل جسم كروي (أي حجم كرة ، لكن يُشار إليه بشكل كلاسيكي بحجم الجسم الكروي)
حيث r هو نصف القطر و d هو قطر المجال. استخلص أرخميدس هذه الصيغة أولاً من خلال إظهار أن الحجم داخل الكرة هو ضعف الحجم بين الجسم الكروي و أسطوانة محيطة من تلك الكرة (التي لها ارتفاع و قطر يساوي قطر الجسم الكروي).[6] يمكن إثبات ذلك عن طريق طبع مخروط رأسًا على عقب إلى نصف الكرة ، مع ملاحظة أن مساحة المقطع العرضي للمخروط بالإضافة إلى مساحة المقطع العرضي للكرة هي نفس مساحة المقطع العرضي للأسطوانة المحدودة. وتطبيق مبدأ كاڤاليري.[7] يمكن أيضًا اشتقاق هذه الصيغة باستخدام حساب متكامل ، أي تكامل القرص لتجميع أحجام عدد لانهائي من أقراص دائرية للأضلاع الصغيرة ذات التجمع غير المحدود. إلى جانب ومركزها على طول x-المحور من x = −r إلى x = r, على افتراض أن مجال نصف القطر r يتمركز في الأصل.
في أي x ، فإن الحجم المتزايد (δV) يساوي ناتج المقطع العرضي مساحة القرص عند x وسمكها (δx):
الحجم الكلي هو مجموع جميع الأحجام الإضافية:
في الحد حيث تقترب δx من الصفر,[8] تصبح هذه المعادلة:
في أي x ، يربط مثلث قائم الزاوية x و y و r بالأصل ؛ وبالتالي ، فإن تطبيق نظرية فيثاغورس يعطي:
باستخدام هذا الاستبدال يعطي
والتي يمكن تقييمها لإعطاء النتيجة
تم العثور على صيغة بديلة باستخدام إحداثيات كروية ، مع عنصر الحجم
لذلك
لمعظم الأغراض العملية ، يمكن تقريب الحجم داخل الكرة المدرج في المكعب بنسبة 52.4 ٪ من حجم المكعب ، حيث V = π/6 d3, حيث d قطر الكرة وكذلك طول جانب المكعب وπ/6 ≈ 0.5236. على سبيل المثال ، الكرة التي يبلغ قطرها 1 m بها 52.4٪ من حجم المكعب بطول الحافة 1 m أو حوالي 0.524 m3.
مساحة السطح
مساحة السطح من دائرة نصف قطرها r:
اشتق أرخميدس هذه الصيغة أولاً[9] من حقيقة أن الإسقاط على السطح الجانبي لاسطوانة المحاطة يحافظ على المساحة.[10] يأتي نهج آخر للحصول على الصيغة من حقيقة أنها تساوي مشتق الصيغة للحجم بالنسبة إلى r لأن الحجم الإجمالي داخل دائرة نصف قطرها r يمكن اعتبارها عبارة عن تجميع مساحة سطح عدد لا نهائي من الأصداف الكروية بسماكة متناهية الصغر مكدسة بشكل مكثف داخل بعضها البعض من نصف القطر 0 إلى نصف القطر r. في السماكة المتناهية الصغر ، يكون التناقض بين مساحة السطح الداخلية والخارجية لأي غلاف معين متناهي الصغر ، وحجم العنصر عند نصف القطر r هو ببساطة ناتج مساحة السطح عند نصف القطر r و سمك متناهية الصغر.
في أي نصف قطر معين r,[note 1] الحجم المتزايد (δV) يساوي ناتج مساحة السطح عند نصف القطرr (A(r)) وسمك المحيط (δr):
الحجم الكلي هو مجموع جميع أحجام المحيط:
في الحد حيث تقترب δr من الصفر[8] تصبح هذه المعادلة:
باستبدال V:
التفريق بين طرفي المعادلة فيما يتعلق بـ r ينتج A كنابع ل r:
يُختصر هذا بشكل عام على النحو التالي:
حيث يعتبر r الآن نصف القطر الثابت للكرة.
بدلاً من ذلك ، يتم إعطاء عنصر المساحة على الكرة في إحداثيات كروية بواسطة dA = r2 sin θ dθ dφ. في إحداثيات ديكارتية عنصر المساحة هو[citation needed]
وبالتالي يمكن الحصول على المساحة الإجمالية عن طريق تكامل:
يحتوي المجال على أصغر مساحة سطح من جميع الأسطح التي تحتوي على حجم معين ، ويحيط أكبر حجم بين جميع الأسطح المغلقة بمساحة سطح معينة.[11]لذلك يظهر المجال في الطبيعة: على سبيل المثال ، الفقاعات وقطرات الماء الصغيرة كروية تقريبًا لأن التوتر السطحي يقلل من مساحة السطح موضعياً.
تسمى المساحة السطحية المتعلقة بكتلة الكرة مساحة السطح المحددة ويمكن التعبير عنها من المعادلات المذكورة أعلاه على أنها: حيث تكون ρ هي الكثافة (نسبة الكتلة إلى الحجم).
منحنيات على دائرة
الدوائر
- تقاطع المجسم الكروي والمستوى عبارة عن دائرة أو نقطة أو فارغة.
في حالة وجود دائرة ، يمكن وصف الدائرة بواسطة معادلة پارامترية : انظر قسم المستوى في القطع ناقص.
لكن الأسطح الأكثر تعقيدًا قد تتقاطع مع كرة في دوائر أيضًا:
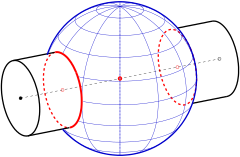
- يتقاطع المجال مع سطح الدوران غير الفارغ ، والذي يحتوي محوره على مركز الكرة ("متحد المحور") يتكون من دوائر و / أو نقاط.
يوضح الرسم البياني الحالة ، حيث يتكون تقاطع الأسطوانة والكرة من دائرتين. هل سيكون نصف قطر الأسطوانة مساويًا لنصف قطر الكرة ، سيكون التقاطع دائرة واحدة ، حيث يكون كلا السطحين متماثلين.
في حالة وجود كرة كروية لها نفس المركز والمحور الرئيسي مثل الكرة ، فإن التقاطع يتكون من نقطتين (القمم) ، حيث تكون الأسطح متماسة.
منحنيات كليليا
إذا تم وصف المجال من خلال تمثيل پارامتري
يحصل المرء على منحنيات كليليا ، إذا كانت الزوايا متصلة بالمعادلة
- منحنيات ڤيڤاني () و دوامة كروية () كحالات خاصة
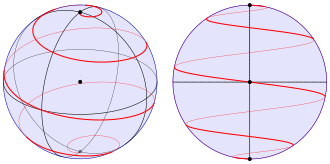
Loxodrome
في الملاحة ، يكون خط البوصلة أو loxodrome عبارة عن قوس يعبر كل خط تنصيف من خطوط الطول في نفس الزاوية. إن الخط المعين ليس دوامة كروية. لا يوجد اتصال بسيط بين الزوايا و .
تداخل كرة مع سطح أكثر عمومية
إذا تداخلت كرة مع سطح آخر ، فقد يكون هناك منحنيات كروية أكثر تعقيدًا.
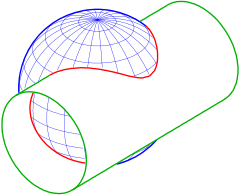
مثال: الكرة - الاسطوانة
تداخل الكرة مع المعادلة واسطوانة بمعادلة ليست مجرد دائرة أو دائرتين. إنه حل نظام المعادلات غير الخطي
(انظر المنحنى الكامن والمخطط)
الخصائص الهندسية
يتم تحديد الجسم الكروي بشكل فريد من خلال أربع نقاط ليست في نفس المستوي. بشكل أعم ، يتم تحديد الجسم الكروي بشكل فريد من خلال أربعة شروط مثل المرور عبر نقطة ، أو التماس في مستوي، وما إلى ذلك.[12] تشبه هذه الخاصية التي تحدد ثلاث نقاط غير متداخلة دائرة فريدة في مستوى.
وبالتالي ، يتم تحديد المجال بشكل فريد من خلال (أي يمر عبر) دائرة ونقطة ليست في مستوى تلك الدائرة.
من خلال بحث الحلول الشائعة لمعادلات الكرتين ، يمكن ملاحظة أن الجسمين الكرويين يتقاطعان في دائرة ويسمى المستوى الذي يحتوي على هذه الدائرة بالمستوي الجذري من الأجسام الكروية المتقاطعة.[13] على الرغم من أن المستوى الجذري هو مستوى حقيقي ، إلا أن الدائرة قد تكون تخيلية (لا توجد نقاط مشتركة بين الكرات الحقيقية) أو تتكون من نقطة واحدة (الكرات متماسسة عند تلك النقطة).[14]
الزاوية بين دائرتين عند نقطة تقاطع حقيقية هي الزاوية الثنائية التي تحددها المستويات المماسّة للكرات عند تلك النقطة. يتقاطع مجالان في نفس الزاوية في جميع نقاط دائرة التقاطع بينهما.[15]تتقاطع عند زوايا قائمة ( متعامدة) إذا وفقط إذا كان مربع المسافة بين مراكزها يساوي مجموع مربعات نصف قطرها.[3]
حزمة من الكرات
إذا f(x, y, z) = 0 و g(x, y, z) = 0 هي معادلات كرتين مستقلتين إذاً
هي أيضًا معادلة الكرة للقيم العشوائية للپارامترات s و t. مجموعة جميع الكرات التي تلبي هذه المعادلة تسمى "حزمة من الكرات" يحددها الكرتان الأصليتان. في هذا التعريف ، يُسمح للكرة بأن تكون مستويًا (نصف القطر اللامتناهي ، المركز في اللانهاية) وإذا كانت كلتا الكراتين الأصلية هي مستويات ، فإن جميع حزم الكرات هي مستويات ، وإلا سيكون هناك مستوى واحد فقط (المستوى الجذري) في الحزمة.[3]
إذا كانت حزمة الكرات لا تتكون من جميع المستويات ، فهناك ثلاثة أنواع من الحزم:[14]
- إذا تقاطعت الكرات في دائرة حقيقية C ، فإن الحزمة تتكون من جميع الكرات التي تحتوي على قالب:Mvar C ، بما في ذلك المستوى الجذري. تقع مراكز جميع الكرات العادية في الحزمة على خط يمر عبر مركز C ويتعامد مع المستوى الجذري.
- إذا كانت الكرات تتقاطع في دائرة تخيلية ، فإن جميع حزم الكرات تمر أيضًا من خلال هذه الدائرة التخيلية ولكنها مفصولة ككرات عادية (ليس لها نقاط حقيقية مشتركة). خط المراكز متعامد مع المستوى الجذري، وهو مستوى حقيقي في حزمة يحتوي على الدائرة التخيلية.
- إذا كانت الكرات تتقاطع في نقطة A ، فإن جميع الكرات في الحزمة تكون متماسة عند A والمستوى الجذري هو المستوى المماس الشائع لجميع هذه الكرات. خط المراكز متعامد مع المستوى الجذري عند A.
جميع الخطوط المماسية من نقطة ثابتة في المستوى الجذري إلى كرات الحزمة لها نفس الطول.[14]
المستوى الجذري هو موضع مراكز جميع الكرات المتعامدة مع جميع الكرات في الحزمة. علاوة على ذلك ، فإن الكرة المتعامدة مع أي كرتين من حزمة الكرات هي متعامدة بالنسبة لهم جميعًا ومركزها يقع في المستوى الجذري للحزمة.[14]
المصطلحات
القطاعات المستوية
وهي عبارة عن "دائرة كبيرة" على الكرة لها نفس المركز ونصف قطر الكرة - وبالتالي تقسيمها إلى قسمين متساويين. تسمى القطاعات المستوية من الكرة "قطاعات كروية -" وهي إما دوائر كبيرة للمستويات من خلال مركز الكرة أو "الدوائر الصغيرة" لباقي الأقسام.[16]
يقسم أي مستو يحتوي على مركز الكرة إلى نصفين كرويين متساويين. أي مستويين متقاطعين يحتويان على مركز الكرة يقسم الكرة إلى أربعة هلالات أو مثلثات ، تتطابق رؤوسها مع نقطة المقابلة تتموضع على خط تقاطع المستويات .
فروع الهندسة
المسافة غير الإقليدية
تسمى أي زوج من النقاط على كرة تقع على خط مستقيم من خلال مركز الكرة (أي القطر) نقاط متقابلة - على الكرة ، تبلغ المسافة بينهما نصف طول المحيط بالضبط. [note 2] أي زوج آخر (أي ليس مقابلاً للقطعة) من نقاط مميزة في المجال
- تقع على دائرة كبيرة فريدة من نوعها ،
- يقسمها إلى قوس ثانوي واحد (أي أقصر) و رئيسي (أي أطول) ، و
- يجعل من طول القوس الصغير هو "أقصر مسافة" بينهما على الكرة. [note 3]
تشترك الهندسة الكروية[note 4] في العديد من الخصائص المماثلة لـ الهندسة الإقليدية و سابقاً مع "مسافة الدائرة العظمى".
الهندسة التفاضلية
وأكثر من ذلك بكثير من التعميم التجريدي للهندسة يستخدم أيضًا نفس مفهوم المسافة في الدائرة الريمانية.
تخمين نصف الكرة ليكون الحشو المتساوي القياس الأمثل (أقل منطقة) من الدائرة الريمانية.
الهندسة الإسقاطية
الخاصية المقابلة للكرة هو السطح المسمى المستوى الإسقاطي الحقيقي ، والذي يمكن اعتباره أيضًا نصف الكرة الشمالي مع تحديد النقاط المقابلة للاستواء.
الجغرافيا
المصطلحات المستعارة مباشرة من جغرافيا الأرض ، على الرغم من أن شكلها كروي وله انحرافات أكبر أو أقل من المجال المثالي (انظر geoid) ، المفهومة جيدًا على نطاق واسع. في الهندسة غير المتعلقة بالأجسام الفلكية ، يجب استخدام مصطلحات مركزية الأرض فقط للتوضيح و"الملاحظة" على هذا النحو ، ما لم يكن هناك فرصة لسوء الفهم.
الأقطاب، خط الطول وخطوط العرض
إذا تم تحديد نقطة معينة على الكرة (بشكل عشوائي) على أنها "القطب الشمالي" ، فإن النقطة المقابلة للقطب تسمى "القطب الجنوبي". الدائرة الكبيرة المتساوية لكل منها هي "خط الاستواء". تسمى الدوائر العظيمة عبر القطبين خطوط خط الطول (أو خطوط اتنصيف). الخط "ليس على الكرة" ولكن من خلال مركزه الذي يربط القطبين "قد" يطلق عليه محور الدوران. الدوائر على الكرة الموازية (أي ليست دوائر كبيرة) إلى خط الاستواء هي خطوط خط العرض.
التعميم للأبعاد الأخرى - طوبولوجيا
- الكرة-0 هي زوج من النقاط تحدد قطعة مستقيمة طولها 2r
- الكرة-1، هي دائرة نصف قطرها r
- الكرة-2 هي الكرة الإعتيادية في الفضاء الثلاثي الأبعاد
- الكرة-3 هي كرة في الفضاء الرباعي الأبعاد.
التعميمات
البعدية
يمكن تعميم الكرات على أي عدد من الأبعاد. لأي الرقم الطبيعي n ، "n - كرة" ، غالبًا ما تتم كتابتها كـ Sn, هي مجموعة النقاط في (n + 1)-الأبعاد الإقليدية التي تكون على مسافة ثابتة r من نقطة مركزية في تلك المساحة ، حيث r ، كما كان من قبل ، رقم حقيقي موجب. خاصه:
- S0: الكرة 0 هي زوج من نقاط النهاية للفاصل [−r, r] من الخط الحقيقي
- S1: الكرة 1 هي دائرة من نصف القطر r
- S2: الكرة 2 هو الكرة العادية
- S3: كرة-3 هي كرة في الفضاء الإقليدي رباعي الأبعاد.
الكرات n > 2 تسمى أحيانًا بـ كرات ذات أبعاد أكثر من ثلاثة.
كرة-n نصف قطر الوحدة المتمركز في الأصل Sn وغالبًا ما يشار إليه باسم كرة-n. لاحظ أن الكرة العادية عبارة عن كرة 2 ، لأنه سطح ثنائي الأبعاد (مضمن في مساحة ثلاثية الأبعاد). مساحة سطح الوحدة (كرة-n-1)
حيث Γ(z) هو أويلر دالة گاما.
تعبير آخر لمساحة السطح
والحجم هو مساحة السطح r/n مرات أو
توجد أيضًا صيغ تكرارية عامة لـ حجم كرة-n.
الفراغات القياسية
بشكل عام، في الفراغ القياسي (E,d)، تكون كرة المركز xونصف القطر r > 0هي مجموعة النقاط y بحيث أن d(x,y) = r.
إذا كان المركز هو النقطة المميزة التي تعتبر أصل E، كما في الفضاء معياري، لم يتم ذكره في التعريف والترميز. الأمر نفسه ينطبق على نصف القطر إذا تم اعتباره مساويًا للواحد، كما في حالة وحدة المجسم الكروي.
على عكس كرة، حتى الكرة الكبيرة قد تكون مجموعة فارغة. على سبيل المثال، في Zn بمقياس إقليدي، تكون كرة نصف قطرها r غير فارغة فقط إذا كان بالإمكان كتابة r2 كمجموع n من مربعات الأعداد الصحيحة.
الطبولوجيا
في الطبولوجيا، يتم تعريف n-كرة iعلى أنه مساحة متجانسة الشكل لحدود كرة-(n + 1); بالتالي، فهو متجانس مع n-الكرة، الإقليدي لكن ربما يفتقر لمقياسه.
- الكرة 0 هي زوج من النقاط مع طوبولوجيا متقطعة.
- الكرة 1 هي دائرة (تصل إلى التماثل)؛ وبالتالي، على سبيل المثال، (صورة) أي عقدة هي كرة 1 !
- الكرة 2 هو كرة عادية (تصل إلى التماثل)؛ وبالتالي، على سبيل المثال، أي مجسم كروي هو كرة 2.
يتم الإشارة لكرة-n ب Sn. فهمي مثال عن متعدد طبولوجي مدمج من دون حدود.لحاجة لأن تكون الكرة سلسة; فإذا كانت سلسة، لا حاجة لأن تكون مختلفة عن الكرة الإقليدية أي (الكرة الشاذة).
تشير نظرية هين-بوريل إلى أن كرة-n الإقليدية مدمجة. فالكرة هي الصورة المعكوسة لمجموعة من نقطة واحدة بحكم الدالة المستمرة ‖x‖. لذلك، فإن الكرة المغلقة تحد Sn أيضاً; لذلك تعتبر أيضاً مدمجة.
من اللافت للنظر ، أنه من الممكن قلب الكرة العادية من الداخل إلى الخارج في فضاء ثلاثي الأبعاد مع إمكانية التقاطعات الذاتية ولكن دون إحداث أي تجعد، في عملية تسمى انقلاب الكرة.
الهندسة الكروية

العناصر الأساسية لـ هندسة المستوى الإقليدي هي النقاط و الخطوط. على الكرة، يتم تحديد النقاط بالمعنى المعتاد. نظير "الخط" هو الجيوديسية، وهو الدائرة العظمى؛ فالسمة المميزة للدائرة العظمى هي أن المستوى الذي يحتوي على جميع نقاطه يمر أيضًا عبر مركز الكرة. يتم القياس بواسطة طول القوس الذي يوضح أن أقصر مسار بين نقطتين ملقاة على الكرة هو الجزء الأقصر من الدائرة العظمى الذي يتضمن النقاط.
تصح العديد من النظريات من الهندسة الكلاسيكية بالنسبة للهندسة الكروية أيضًا، ولكن ليس جميعها كذلك لأن الكرة فشلت في تلبية بعض افتراضات الهندسة الكلاسيكية، بما في ذلك فرضية التوازي. في حساب المثلثات الكروية، يتم تعريف الزاوية بين الدوائر العظمى. حيث يختلف علم المثلثات الكروي عن علم المثلثات العادي في كثير من النواحي. على سبيل المثال، مجموع الزوايا الداخلية لـ مثلث كروي يتجاوز دائمًا 180 درجة. وأيضًا، يكون أي مثلثان كرويان متشابهان متطابقان.
الخصائص الاحدى عشر للكرة
في كتابهم (الهندسة والتصور)[17] يصف كل من ديڤد هيلبرت و ستيفان كون ڤوسن إحدى عشرة خاصية للكرة ومناقشة ما إذا كانت هذه الخصائص تحدد الكرة بشكل فريد. تدعم العديد من الخصائص المستوى، والذي يمكن اعتباره كروياً ذو نصف قطر لانهائي. هذه الخصائص هي:
- جميع النقاط على الكرة هي نفس المسافة من نقطة ثابتة. كما أن نسبة مسافة نقطته من نقطتين ثابتتين هي نسبة ثابتة.
- الجزء الأول هو التعريف المعتاد للكرة ويحددها بشكل فريد. الجزء الثاني يمكن استنتاجه بسهولة ويتبع نتيجة من أپولونيوس پيرگا لـ الدائرة. ينطبق هذا الجزء الثاني أيضًا على المستوي.
- يكون محيط الكرة وأقسامها المستوية دوائراً
- هذه الخاصية تحدد الكرة بشكل فريد.
- للكرة عرض ثابت ومحيط ثابت.
- عرض السطح هو المسافة بين أزواج مستويات الظل المتوازية. العديد من الأسطح المحدبة المغلقة الأخرى لها عرض ثابت، على سبيل المثال جسم مايسنر. محيط السطح هو محيط حدود الإسقاط المتعامد على مستوى. كل من هذه الخصائص تعني الآخر.
- جميع نقاط الكرة هي سرية.
- في أي نقطة على سطح ما، يكون الاتجاه الطبيعي بزاوية قائمة على السطح لأن الكرة هذه هي الخطوط التي تنتشر من مركز الكرة. سيشكل تقاطع المستوى الذي يحتوي على المستوى الطبيعي مع السطح منحنى يسمى القسم الطبيعي، ويكون انحناء هذا المنحنى هو الانحناء الطبيعي. بالنسبة لمعظم النقاط على معظم الأسطح، سيكون للأقسام المختلفة انحناءات مختلفة؛ القيم العظمى والدنيا لهذه تسمى الانحناءات الرئيسي. أي سطح مغلق سيكون به أربع نقاط على الأقل تسمى "نقاط سرية". في السرة، تكون جميع الانحناءات المقطعية متساوية؛ على وجه الخصوص، الانحناءات الرئيسي متساوية. يمكن اعتبار النقاط السرية على أنها النقاط التي يتم فيها تقريب السطح بواسطة كرة.
- بالنسبة للكرة، تكون الانحناءات في جميع الأقسام العادية متساوية، لذا فإن كل نقطة عبارة عن سرة. الكرة والمستوي هما السطحان الوحيدان لهذه الخاصية.
- لا تحتوي الكرة على سطح من المراكز.
- بالنسبة لقسم طبيعي معين، توجد دائرة انحناء تساوي الانحناء المقطعي، وهي مماس للسطح، وتقع خطوط المركز على طول الخط الطبيعي. على سبيل المثال، يطلق على المركزين المتوافقين مع الانحناءات المقطعية القصوى والدنيا اسم نقاط المركز، وتشكل مجموعة كل هذه المراكز السطح المركزي.
- بالنسبة لمعظم الأسطح ، يشكل السطح المركزي لوحين كل منهما سطح ويلتقيان عند النقاط السرية. توجد عدة حالات خاصة:
- * بالنسبة إلى أسطح القناة يشكل لوح واحدة منحنى واللوح الآخر عبارة عن سطح
- * بالنسبة إلى المخاريط، الإسطوانات، النتوءات المستديرة و سيكليدات يشكل كلا اللوحين منحنيات.
- * بالنسبة للكرة، يقع مركز كل دائرة متذبذبة في مركز الكرة ويشكل السطح المركزي نقطة واحدة. هذه الخاصية هي فريدة من نوعها في خواص الكرة.
- جميع الجيوديسيا للكرة هي منحنيات مغلقة.
- الجيوديسية هي منحنيات على سطح تعطي أقصر مسافة بين نقطتين. إنها تعميم لمفهوم الخط المستقيم في المستوى. بالنسبة للكرة، تعتبر الجيوديسيا دوائر كبيرة. والعديد من الأسطح الأخرى تشترك في هذه الخاصية.
- من بين جميع المواد الصلبة التي لها حجم معين، فإن الكرة هي أصغر مساحة سطح؛ من بين جميع المواد الصلبة التي لها مساحة سطح معينة، فإن الكرة هي التي لها أكبر حجم.
- يتبع من المتباينة متساوية. تحدد هذه الخصائص الكرة بشكل فريد ويمكن رؤيتها في فقاعة الصابون: ستنحصر فقاعة الصابون بحجمًا ثابتًا، ويقلل التوتر السطحي مساحة سطحها لهذا الحجم. لذلك، فإن فقاعة الصابون العائمة بحرية تقترب من كرة (على الرغم من أن قوى خارجية مثل الجاذبية ستشوه شكل الفقاعة قليلاً). يمكن رؤيته أيضًا في الكواكب والنجوم حيث تعمل الجاذبية على تقليل مساحة سطح الأجرام السماوية الكبيرة.
- الكرة لديها أصغر متوسط انحناء إجمالي بين جميع المواد الصلبة المحدبة مع مساحة سطح معينة.
- متوسط الانحناء هو متوسط الانحناءين الرئيسيين، وهو ثابت لأن الانحناءين الرئيسيين ثابتان في جميع نقاط الكرة.
- للكرة انحناء متوسط ثابت.
- الكرة هي السطح الوحيد المضمن الذي يفتقر إلى الحدود أو التميزات مع انحناء متوسط إيجابي ثابت. الأسطح المغمورة الأخرى مثل الحد الأصغري من السطح لها متوسط انحناء ثابت.
- للكرة انحناء گاوسي إيجابي ثابت.
- انحناء الگاوسي هو ناتج تقوسين رئيسيين. إنها خاصية جوهرية يمكن تحديدها عن طريق قياس الطول والزوايا وهي مستقلة عن كيفية أن المساحة مضمنة في الفراغ. ومن ثم ، فإن ثني السطح لن يغير الانحناء الگاوسي، ويمكن الحصول على الأسطح الأخرى ذات الانحناء الگاوسي الإيجابي الثابت عن طريق قطع شق صغير في الكرة وثنيها. كل هذه الأسطح الأخرى سيكون لها حدود، والكرة هي السطح الوحيد الذي يفتقر إلى حدود مع انحناء گاوسي ثابت وإيجابي. الكرة الزائفة هي مثال لسطح به انحناء گاوسي سلبي ثابت.
- يتم تحويل الكرة إلى نفسها من خلال عائلة مكونة من ثلاثة پارامترات من الحركات الصلبة.
- بالدوران حول أي محور، ستعمل وحدة المجال في الأصل على تعيين الكرة على نفسها. يمكن التعبير عن أي دوران حول خط عبر الأصل كمجموعة من الدورات حول المحور ذي الإحداثيات الثلاثة (انظر زوايا أويلر). لذلك، توجد عائلة من الدورات ثلاثية الپارامترات بحيث يحول كل دوران الكرة إلى نفسها؛ هذه العائلة هي مجموعة الدوران SO (3). المستوى هو السطح الآخر الوحيد الذي يحتوي على عائلة تحويلات مكونة من ثلاثة پارامترات (تحويلات على طول المحاور x - و y ودورات حول الأصل). الأسطوانات الدائرية هي الأسطح الوحيدة ذات العائلات ذات الپارامترين من الحركات الصلبة و أسطح الدوران و الهليكويد هي الأسطح الوحيدة مع عائلة ذات پارامتر واحد.
المناطق
انظر أيضاً
- 3-الكرة
- Affine sphere
- Alexander horned sphere
- القبة السماوية
- مكعب
- انحناء
- احصائيات متجهية
- Dome (mathematics)
- Dyson sphere
- Hand with Reflecting Sphere, M.C. Escher self-portrait drawing illustrating reflection and the optical properties of a mirror sphere
- Hoberman sphere
- Homology sphere
- Homotopy groups of spheres
- Homotopy sphere
- Hypersphere
- Lenart Sphere
- Napkin ring problem
- Orb (optics)
- Pseudosphere
- Riemann sphere
- Solid angle
- Sphere packing
- Spherical coordinates
- Spherical Earth
- Spherical helix, tangent indicatrix of a curve of constant precession
- Spherical shell
- Sphericity
- Zoll sphere
معرض الصور
صورة لواحد من أكثر المجالات دقة من صنع الإنسان، حيث انكسار صورة أينشتاين في الخلفية. هذه الكرة كانت جيروسكوب كوارتز مدمج لتجربة مسبار الجاذبية ب، وتختلف في الشكل عن الكرة المثالية بما لا يزيد عن 40 ذرة (أقل من 10 nm) سماكة. تم الإعلان في 1 يوليو 2008 أن علماء أستراليا قاموا بإنشاء مجالات شبه مثالية، بدقة تصل إلى 0.310 nm، كجزء من مطاردة بحثية دولية لإيجاد معيار عالمي جديد للكيلوگرام
ظهر ورق لعب يوضح الآلات الهندسية، إنگلترا، 1702. كرات ملك البستوني:
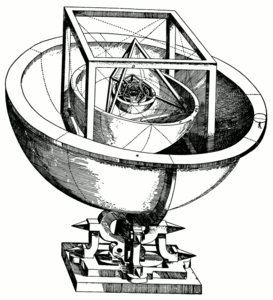
"قدح كپلر": نموذج للمجموعة الشمسية من خمس عديدات الأوجه منتظمة والكريات المحاطة بهم والكريات المحيطة بهم.
استخدام الكرة في العمارة: قبو نصف كروي مضلع لقبة في المسجد الجامع بالقيروان (في تونس ).
الهوامش والمصادر
الهوامش
- ^ r يتم اعتباره متغيرًا في هذا الحساب.
- ^ It does not matter which direction is chosen, the distance is the sphere's radius × π.
- ^ The distance between two non-distinct points (i.e. a point and itself) on the sphere is zero.
- ^ Despite not being flat, a sphere is two-dimensional since it comprises only the surface of a solid ball.
المصادر
- ^ أ ب Albert 2016, p. 54.
- ^ أ ب ت خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةEB - ^ أ ب ت Woods 1961, p. 266.
- ^ Kreyszig (1972, p. 342).
- ^ Albert 2016, p. 60.
- ^ Steinhaus 1969, p. 223.
- ^ "The volume of a sphere - Math Central". mathcentral.uregina.ca. Retrieved 2019-06-10.
- ^ أ ب E.J. Borowski; J.M. Borwein. Collins Dictionary of Mathematics. pp. 141, 149. ISBN 978-0-00-434347-1.
- ^ Eric W. Weisstein, Sphere at MathWorld.
- ^ Steinhaus 1969, p. 221.
- ^ Osserman, Robert (1978). "The isoperimetric inequality". Bulletin of the American Mathematical Society. 84: 1187. Retrieved 14 December 2019.
- ^ Albert 2016, p. 55.
- ^ Albert 2016, p. 57.
- ^ أ ب ت ث Woods 1961, p. 267.
- ^ Albert 2016, p. 58.
- ^ Eric W. Weisstein, Spheric section at MathWorld.
- ^ Hilbert, David; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (2nd ed.). Chelsea. ISBN 978-0-8284-1087-8.
قراءات إضافية
- Albert, Abraham Adrian (2016) [1949], Solid Analytic Geometry, Dover, ISBN 978-0-486-81026-3.
- Dunham, William (1997). The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems and Personalities. New York. pp. 28, 226. Bibcode:1994muaa.book.....D. ISBN 978-0-471-17661-9.
{{cite book}}:|journal=ignored (help)CS1 maint: location missing publisher (link) - Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley, ISBN 978-0-471-50728-4, https://archive.org/details/advancedengineer00krey.
- Steinhaus, H. (1969), Mathematical Snapshots (Third American ed.), Oxford University Press.
- Woods, Frederick S. (1961) [1922], Higher Geometry / An Introduction to Advanced Methods in Analytic Geometry, Dover.
وصلات خارجية
- Short description is different from Wikidata
- Articles with hatnote templates targeting a nonexistent page
- Missing redirects
- Articles with unsourced statements from February 2019
- CS1 errors: periodical ignored
- CS1 maint: location missing publisher
- كرات
- طوبولوجيا تفاضلية
- أشكال ابتدائية
- Homogeneous spaces
- هندسة ابتدائية
- هندسة تفاضلية
- سطوح
- طوبولوجيا
























![{\displaystyle V=\pi \left[r^{2}x-{\frac {x^{3}}{3}}\right]_{-r}^{r}=\pi \left(r^{3}-{\frac {r^{3}}{3}}\right)-\pi \left(-r^{3}+{\frac {r^{3}}{3}}\right)={\frac {4}{3}}\pi r^{3}.}](https://www.marefa.org/api/rest_v1/media/math/render/svg/4c081de9760153a5ab7e59be1b9de1aa97d08dec)