سرعة زاوية

السرعة الزاوية تعبر عن سرعة دوران وجهة الدوران حول المحور

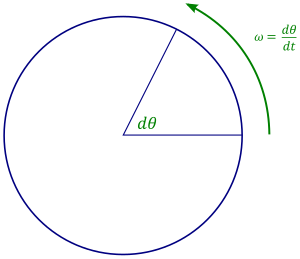
في الفيزياء، السرعة الزاوية (إنگليزية: angular velocity) هي كمـّيـّة سـُلـَّمـِـيـّة (scalar quantity)، وتلك تعتبر كمـّيـّة ساذجة في نوعها التي تعبـّر عن التردد الزاوي وتصف دوران المحور الذي يدور من حوله أي جسم ما. وحدة قياس السرعة الزاوية في نظام الوحدات الدولي هي الراديان في الثانية، ومن الممكن قياسها بواحدات أخرى مثل درجة في الثانية. عندما تقاس بواحدة دورة في واحدة الزمن (دورة في الدقيقة...الخ) فإنه يطلق عليها اسم السرعة الدورانية. يرمز للسرعة الزاوية بالحرف أوميغا (Ω أو ω). جهة متجهة السرعة الزاوية تكون عمودية على مستوي الدوران، والتي تحدد غالباً باستخدام قاعدة اليد اليمنى.

وعلى اعتبار أن كل دورة تعادل 2π راديان ينتج لدينا العلاقة: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = {{2 \pi} \over T} = {2 \pi f} = \frac {v} {r} }

حيث

ω التردد الزاوي (راديان في الثانية)

T الزمن (ثانية)

f التردد (هيرتز)

v السرعة المماسية لنقطة حول محور الدوران (متر في الثانية)

r نصف قطر الدوران (متر)

أي أنّ التردد الزاوي ما هو إلاّ مضاعفة للتردّد العادي. مع هذا، فيستحسن استخدام التردد الزاوي عوضًا عن العادي في بعض المجالات التي فيها الظواهر الدورانية شائعة، كالكهرومغناطيسيّة أو ميكانيكا الكم، لأنّ بهذا التمثيل بالامكان الاستغناء عن الـخطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} .

 أمثلة

فعلى سبيل المثال، تكون العلاقة بين التسارع a والإزاحة x علاقة خطيّة عكسية، بحيث يكون المعامل الخطي هو تربيع التردد الزاوي خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} :

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = -\omega ^2 x \;}

أما في التمثيل العادي للتردد:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = -4 \pi f^2 x \;}

كذلك، في حركة نابض توافقية (بدون احتكاك أو تخميد)، تتحقّق العلاقة التالية بين التسارع الزاوي، $\omega$، كتلة الجسم المربوط، m، وثابت النابض، k:

$\omega ={\frac {k}{m}}$

ويسمّى هذا التردد، حتّى مع وجود احتكاك أو تخميد، التردد الطبيعي للجهاز أو الجسم.

أمّا في دائرة كهربائية تحتوي على مكثف وملف، فيكون التردد الطبيعي كالتالي:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = \frac {1} {\sqrt{LC}} \;}

حيث يمثل C سعة المكثف (بوحدات فاراد)، ويمثل L استحثاث الملف (بوحدات هنري).

 انظر أيضاً

• تردد زاوي
• تسارع زاوي
• عزم زاوي