تدفق مغناطيسي

كهرومغناطيسية

كهرباء • مغناطيسية كهروستاتيكية  · شحنة كهربائية · قانون كولوم · مجال كهربائي · تدفق كهربائي · قانون گاوس · كمون كهربائي · حث كهروستاتيكي · عزم ثنائي القطب كهربائي · استاتيكا مغناطيسية  · قانون أمبير · تيار كهربائي  · مجال مغناطيسي · تدفق مغناطيسي · قانون بيو-ساڤار · عزم مغناطيسي · قانون گاوس للمغناطيسية · ديناميكا كهربائية  · Free space · قانون قوة لورنتس · قوة محركة كهربائية · حث كهرومغناطيسي · قانون فاراداي · قانون لنز · تيار الإزاحة · معادلات ماكسويل · مجال كهرومغناطيسي · إشعاع كهرومغناطيسي · Liénard-Wiechert Potentials · Maxwell tensor · تيار دوامي · شبكة كهربائية  · توصيل كهربائي · مقاومة كهربائية · سعة كهربية · حث كهربي · معاوقة · فجوات رنانة · مرشد الموجة · Covariant formulation  · Electromagnetic tensor · EM Stress-energy tensor · Four-current · Four-potential · العلماء  · أمپير · كولوم · فاراداي · هيڤيسايد · هنري · هرتز · لورنتس · ماكسويل · تسلا · وبر · · غيرهم

التدفق المغناطيسي خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi} الذي يعبر سطح خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}} هو عدد خطوط الحقول المغناطيسي خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{B}} والتي تعبر السطح خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}} و يعبر عنه بالجداء السلمي لشعاع الحقل المغناطيسي خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{B}} و شعاع السطح خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}}

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi = \vec{B}.\vec{S} = \left|B\right|\left|S\right|cos(\alpha) }

واحده التدفق المغناطيسي هي الويبر Weber، تكريما للفيزيائي الألماني ڤيلهلم ويبر [1804-1891] Wilhelm Eduard Weber.

التدفق المغناطيسي عبارة عن قياس للمغناطيسية مع أخذ قوة و شدة الحقل المغناطيسي بالحسبان.

 الوصف

Figure 1: The definition of surface integral relies on splitting the surface into small surface elements. Each element is associated with a vector dS of magnitude equal to the area of the element and with direction normal to the element and pointing outward.

Figure 2: A vector field of normals to a surface.

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \Phi_m = \mathbf{B} \cdot \mathbf{a} = Ba \cos \theta}    (uniform B with flat area only)

where θ is the angle between B and a vector a that is perpendicular (normal) to the surface.

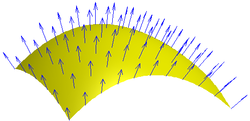
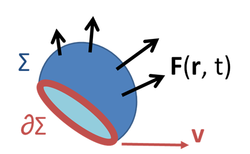
In the general case, the magnetic flux through a surface S is defined as the integral of the magnetic field over the area of the surface (See Figures 1 and 2):

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_m = \iint\limits_S \mathbf{B} \cdot d\mathbf S,}

where خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textstyle \Phi_m \ } is the magnetic flux, B is the magnetic field,

S is the surface (area),$\cdot$ denotes dot product, and dS is an infinitesimal vector, whose magnitude is the area of a differential element of S, and whose direction is the surface normal. (See surface integral for more details.)

From the definition of the magnetic vector potential A and the fundamental theorem of the curl the magnetic flux may also be defined as:

$\Phi _{m}=\oint \limits _{\Sigma }\mathbf {A} \cdot d{\boldsymbol {\ell }}$

where the closed line integral is over the boundary of the surface and dℓ is an infinitesimal vector element of that contour Σ.

The magnetic flux is usually measured with a fluxmeter. The fluxmeter contains measuring coils and electronics that evaluates the change of voltage in the measuring coils to calculate the magnetic flux.

 Magnetic flux through a closed surface

Some examples of closed surfaces (left) and open surfaces (right). Left: Surface of a sphere, surface of a torus, surface of a cube. Right: Disk surface, square surface, surface of a hemisphere. (The surface is blue, the boundary is red.)

المقالة الرئيسية: Gauss's law for magnetism

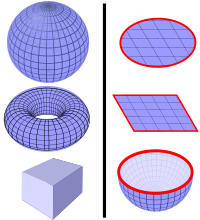
In other words, Gauss's law for magnetism is the statement:

$\Phi _{m}=\int \!\!\!\int \mathbf {B} \cdot d\mathbf {S} =0,$

for any closed surface S.

 Magnetic flux through an open surface

المقالة الرئيسية: Faraday's law of induction

Figure 3: A vector field F ( r, t ) defined throughout space, and a surface Σ bounded by curve ∂Σ moving with velocity v over which the field is integrated.

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E} = \oint_{\partial \Sigma (t)}\left( \mathbf{E}( \mathbf{r},\ t) +\mathbf{ v \times B}(\mathbf{r},\ t)\right) \cdot d\boldsymbol{\ell} = -{d\Phi_m \over dt},}

حيث (انظر الشكل 3):

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}} is the EMF,

Φ_m is the flux through a surface with an opening bounded by a curve ∂Σ(t),

∂Σ(t) is a closed contour that can change with time; the EMF is found around this contour, and the contour is a boundary of the surface over which Φ_m is found,

dℓ is an infinitesimal vector element of the contour ∂Σ(t),

v is the velocity of the segment dℓ,

E is the electric field,

B is the magnetic field.

 مقارنة مع الفيض الكهربائي

المقالة الرئيسية: Electric flux and قانون گاوس

By way of contrast, Gauss's law for electric fields, another of Maxwell's equations, is

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_E = \int \!\!\!\int_S \mathbf{E}\cdot d\mathbf{S} = {Q \over \epsilon_0},}

حيث

E is the electric field,

S is any closed surface,

Q is the total electric charge inside the surface S,

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_0 } is the electric constant (a universal constant, also called the "permittivity of free space").

 انظر أيضاً

• مجال مغناطيسي
• Maxwell's equations (sometimes called the Maxwell equations) are the set of four equations, attributed to James Clerk Maxwell, that describe the behavior of both the electric and magnetic fields, as well as their interactions with matter.
• Gauss's law gives the relation between the electric flux flowing out a closed surface and the electric charge enclosed in the surface.
• Magnetic circuit is a method using an analogy with electric circuits to calculate the flux of complex systems of magnetic components.
• Magnetic monopole is a hypothetical particle that may be loosely described as "a magnet with only one pole".
• Magnetic flux quantum is the quantum of magnetic flux passing through a superconductor.
• Carl Friedrich Gauss developed a fruitful collaboration with the physics professor Wilhelm Weber; it led to new knowledge in the field of magnetism.
• James Clerk Maxwell demonstrated that electric and magnetic forces are two complementary aspects of electromagnetism.

 وصلات خارجية

براءات اختراع

• Vicci, U.S. Patent 6٬720٬855, Magnetic-flux conduits
• Magnetic Flux through a Loop of Wire by Ernest Lee, Wolfram Demonstrations Project.