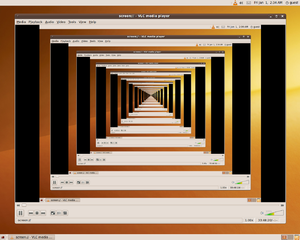
استدعاء ذاتي

صيغة مرئية للاستدعاء الذاتي المعروف بإسم تأثير دروسته. السيدة في تلك الصورة تمسك بغرض يحتوي على صورة أصغر لها ممسكة بنفس الغرض، والتي بدورها تحتوي على صورة أصغر لها ممسكة بنفس الغرض، وهلم جرا.

استدعاء ذاتي إنگليزية: Recursion يعني تكرار الشيء، ويستخدم هذا المصطلح في الرياضيات وفي علوم الحاسوب ليعني تكرار التعريف للدالة نفسها. ويستخدم لتكرار الدالة مرة ثانية وإذا تمت عملية الاستدعاء الذاتي لمرة ثالثة يكرر نفس الشي. وعملية الاستدعاء الذاتي هي إستدعاء الشيء لنفسه. وفي البرمجة عندما تتم عملية الاستدعاء الذاتي للدالة أبجد فيتم كتابتها مرة ثانية وهكذا.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التعريفات الشكلية للاستدعاء الذاتي

Recursion in a screen recording program, where the smaller window contains a snapshot of the entire screen.

ونفس الأمر بالنسبة للبرمجة ففرضا لدينا الدالة Function التالية GetChile(ID)

هذا التابع يقوم بإرجاع كل العناصر للعنصر الأب ذو رقم التعريف ID وعندما يتم تنفيذ التابع فإننا نبحث عن كل أبناء العنصر المطلوب وعند إرجاع كل عنصر ابن نطلب نفس التابع ولكن مع وضع رقم تعريف العنصر الابن وفي حال كان العنصر الأب لا يحوي عناصر أبناء لا نعيد شيء وهكذا حتى نستعيد شجرة بكل العناصر.

 الاستدعاء الذاتي في الرياضيات

استدعاء ذاتي لمثلثات محصورة في مثلث سيرپنسكي لتشكل عقد هندسي.

 فئات معرَّفة بالاستدعاء الذاتي

المقالة الرئيسية: Recursive definition

 مثال: الأعداد الطبيعية

المثال القانوني للفئة المعرفة بالاستدعاء الذاتي تعطيه الأعداد الطبيعية:

1 is in $\mathbb {N}$

فلو n هي في $\mathbb {N}$، فإذن n + 1 is in $\mathbb {N}$

The set of natural numbers is the smallest set satisfying the previous two properties.

 مثال: فئة التقارير التي يمكن الوصول إليها بحق

Another interesting example is the set of all "true reachable" propositions in an axiomatic system.

 الاستدعاء الذاتي في علم الحاسب

This screenshot of a web page includes the screen shot itself.

المقالة الرئيسية: الاستدعاء الذاتي (علم الحاسب)

 مبرهنة الاستدعاء الذاتي

في نظرية الفئات، فهذه هي مبرهنة تضمن وجود الدوال المعرفة باستخدام الدوال المعرفة بالاستدعاء الذاتي. فلو افترضنا أن لدينا X، وهو عنصر a في X والدالة $f:X\rightarrow X$، المبرهنة تقول أنه هناك دالة فريدة $F:\mathbb {N} \rightarrow X$ (حيث $\mathbb {N}$ تشير إلى فئة الأعداد الطبيعية بما فيها صفر) بحيث

$F(0)=a$

$F(n+1)=f(F(n))$

لأي عدد طبيعي n.

 برهان التفرد

Take two functions $F:\mathbb {N} \rightarrow X$ and $G:\mathbb {N} \rightarrow X$ بحيث:

$F(0)=a$

$G(0)=a$

$F(n+1)=f(F(n))$

$G(n+1)=f(G(n))$

حيث a هي عنصر في X.

ويمكن الاثبات باستخدام الاستقراء الرياضي أن $F(n)=G(n)$ لكل الأعداد الطبيعية n:

الحالة الأساسية: $F(0)=a=G(0)$ لذلك فالتساوي ساري لحالة $n=0$.

Inductive Step: افترض $F(k)=G(k)$ لبعض $k\in \mathbb {N}$. Then $F(k+1)=f(F(k))=f(G(k))=G(k+1).$

Hence F(k) = G(k) implies F(k+1) = G(k+1).

By Induction, $F(n)=G(n)$ for all $n\in \mathbb {N}$.

 أمثلة

بعض علاقات الاستدعاء الذاتي الشائعة هي:

• Factorial: $n!=n(n-1)!=n(n-1)\cdots 1$
• Fibonacci numbers: $f(n)=f(n-1)+f(n-2)$
• Catalan numbers: $C_{0}=1$, $C_{n+1}=(4n+2)C_{n}/(n+2)$
• Computing compound interest
• The Tower of Hanoi
• Ackermann function

 انظر أيضاً

• Church-Turing thesis
• Continuous predicate
• Corecursion
• Course-of-values recursion
• Fixed point combinator
• Infinite loop
• Infinitism
• Iterated function
• Mise en abyme
• Primitive recursive function
• Reentrant (subroutine)
• Self-reference
• Strange loop
• Tail recursion
• Turtles all the way down
• Viable System Model

 وصلات خارجية

ابحث عن recursivity في
قاموس المعرفة.

• Johnsonbaugh, Richard (2004). Discrete Mathematics. Prentice Hall. ISBN 0-13-117686-2.
• Hofstadter, Douglas (1999). Gödel, Escher, Bach: an Eternal Golden Braid. Basic Books. ISBN 0-465-02656-7.
• Shoenfield, Joseph R. (2000). Recursion Theory. A K Peters Ltd. ISBN 1-56881-149-7.
• Causey, Robert L. (2001). Logic, Sets, and Recursion. Jones & Bartlett. ISBN 0-7637-1695-2.
• Cori, Rene; Lascar, Daniel; Pelletier, Donald H. (2001). Recursion Theory, Godel's Theorems, Set Theory, Model Theory. Oxford University Press. ISBN 0-19-850050-5.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Barwise, Jon; Moss, Lawrence S. (1996). Vicious Circles. Stanford Univ Center for the Study of Language and Information. ISBN 0-19-850050-5.{{cite book}}: CS1 maint: multiple names: authors list (link) - offers a treatment of corecursion.
• Rosen, Kenneth H. (2002). Discrete Mathematics and Its Applications. McGraw-Hill College. ISBN 0-07-293033-0.
• Cormen, Thomas H., Charles E. Leiserson, Ronald L. Rivest, Clifford Stein (2001). Introduction to Algorithms. Mit Pr. ISBN 0-262-03293-7.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Kernighan, B.; Ritchie, D. (1988). The C programming Language. Prentice Hall. ISBN 0-13-110362-8.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Stokey, Nancy,; Robert Lucas; Edward Prescott (1989). Recursive Methods in Economic Dynamics. Harvard University Press. ISBN 0674750969.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Hungerford; title=Algebra (1980). Springer. ISBN 978-0387905181. {{cite book}}: Missing or empty |title= (help); Missing pipe in: |author= (help)CS1 maint: multiple names: authors list (link), first chapter on set theory.
• Recursion - tutorial by Alan Gauld
• A Primer on Recursion- contains pointers to recursion in Formal Languages, Linguistics, Math and Computer Science
• Zip Files All The Way Down
• Nevins, Andrew and David Pesetsky and Cilene Rodrigues. Evidence and Argumentation: A Reply to Everett (2009). Language 85.3: 671--681 (2009)
• Kaan, E. – Swaab, T. Y. (2002) “The brain circuitry of syntactic comprehension”, Trends in Cognitive Sciences, vol. 6, Issue 8, 350-356.