مسافة الدائرة الكبرى

هذا المقال هو عن shortest-distance on a sphere. إذا كنت تريد the shortest distance on an ellipsoid، انظر geodesics on an ellipsoid.

A diagram illustrating great-circle distance (drawn in red) between two points on a sphere, P and Q. Two antipodal points, u and v are also shown.

طريق الدائرة الكبرى أقرب مسافة بين نقطتين على سطح الأرض. يشير نوع من الخرائط (أعلى) باسم خريطة الإسقاط المماسي المركزي إلى طريق الدائرة الكبرى على أنه خط مستقيم. أما أي خريطة أخرى بما فيها خريطة مركاتور (أسفل) فلا تبّين ذلك.

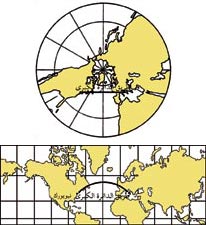
مسافة الدائرة الكبرى Great-circle distance طريقُ الدَّائرة الكُبرى أقصر طريق بين نقطتين على سطح الأرض وأكثرها استقامة. والدَّائرة الكبرى أيُّ دائرة تقسم الكرة الأرضية إلى نصفين متساويين، طولها هو طول خط الاستواء. ويبدو على أغلب الخرائط المسطحة أن الخط المستقيم هو أقصر مسافة بين مكانين. ويظهر طريق الدائرة الكبرى غالبًا على شكل مُنْحَنى طويل. ولكن الخرائط ليست الصورة الحقيقية لسطح الأرض. فالخرائط مسطحة والأرض كرويَّة، لذا فإن أقصر مسافة بين نقطتين على الأرض يمكن أن تجدها بسهولة على الكرة الأرضية فقط. إن أقصر المسافات تقع على طول الدائرة الكبرى التي تمُّر على النقطتين. وهناك نوع خاص من الخرائط يسمى خريطة الإسقاط المماسي المركزي (المسقط المزولي) يشير إلى طريق الدائرة الكبرى كخط مستقيم.

ولاتِّباع طريق الدائرة الكبرى حرفيًا، لابد للسفينة كل حين أن تغير اتجاه بوصلتها إلى الوجهة المُتَّجهة إليها. ويجد الملاح صعوبة في تتبع التَّغير السريع. وبدلاً من ذلك يمكن للملاّح أن يحكم خط السير بسلسلة من الخطوط المتصلة يتبع كل خط وجهة محددة. وتُسمى هذه الخطوط: اتجاهات البوصلة، وتربط بين النُّقط المختارة عبر طريق الدائرة الكبرى. وباتباع اتجاهات البوصلة يمكن للسفينة أن تبحر في الاتجاه الأقرب لأقصر طريق ممكن.

ويمكن للطائرات اتباع طريق الدائرة الكبرى بسهولة أكبر مما تستطيعه السفن. فكثير من الطائرات تتبع نظامًا ملاحيًا يعرف باسم التَّوجيه بالقصور الذاتي وهذا النظام يسمح للطائرة باتباع طريق الدائرة الكبرى بدقة. وتستخدم القذائف الصاروخية أيضًا نظام التوجيه الذاتي في تَتَبُّع طريق الدائرة الكبرى، وهي تدخل الفضاء وتعود للأرض.

 الصيغ

An illustration of the central angle, Δσ, between two points, P and Q. λ and φ are the longitudinal and latitudinal angles of P respectively

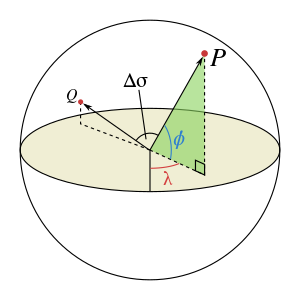
Let $\lambda _{1},\phi _{1}$ and $\lambda _{2},\phi _{2}$ be the geographical longitude and latitude of two points 1 and 2, and $\Delta \lambda ,\Delta \phi$ be their absolute differences; then $\Delta \sigma$, the central angle between them, is given by the spherical law of cosines if one of the poles is used as an auxiliary third point on the sphere:

$\Delta \sigma =\arccos {\bigl (}\sin \phi _{1}\sin \phi _{2}+\cos \phi _{1}\cos \phi _{2}\cos \Delta \lambda {\bigr )}.$

The problem is normally expressed in terms of finding the central angle $\Delta \sigma$. Given this angle in radians, the actual arc length d on a sphere of radius r can be trivially computed as

$d=r\,\Delta \sigma .$

 العلاقة بين الزاوية المركزية وطول القوس

The central angle $\Delta \sigma$ is related with the chord length of unit sphere $\Delta \sigma _{\text{c}}\,\!$:

${\begin{aligned}\Delta \sigma &=2\arcsin {\frac {\Delta \sigma _{\text{c}}}{2}},\\\Delta \sigma _{\text{c}}&=2\sin {\frac {\Delta \sigma }{2}}.\end{aligned}}$

For short-distance approximation ($|\Delta \sigma _{\text{c}}|\ll 1$),

$\Delta \sigma =\Delta \sigma _{\text{c}}\left(1+{\frac {1}{24}}\left(\Delta \sigma _{\text{c}}\right)^{2}+\cdots \right).$

 الصيغ الحاسوبية

On computer systems with low floating point precision, the spherical law of cosines formula can have large rounding errors if the distance is small (if the two points are a kilometer apart on the surface of the Earth, the cosine of the central angle is near 0.99999999). For modern 64-bit floating-point numbers, the spherical law of cosines formula, given above, does not have serious rounding errors for distances larger than a few meters on the surface of the Earth.

The following haversine formula is numerically better-conditioned for small distances based on the above chord-length relation:

${\begin{aligned}\Delta \sigma &=\operatorname {archav} \left(\operatorname {hav} \left(\Delta \phi \right)+\left(1-\operatorname {hav} (\Delta \phi )-\operatorname {hav} (\phi _{1}+\phi _{2})\right)\operatorname {hav} \left(\Delta \lambda \right)\right).\end{aligned}}$

Historically, the use of this formula was simplified by the availability of tables for the haversine function defined by $\operatorname {hav} \theta =\sin ^{2}{\frac {\theta }{2}}$ and $\operatorname {archav} x=2\arcsin {\sqrt {x}}$.

The following shows the equivalent formula expressing the chord length explicitly:

${\begin{aligned}\Delta \sigma _{\text{c}}&=2{\sqrt {\sin ^{2}\left({\frac {\Delta \phi }{2}}\right)+\cos {\phi _{1}}\cdot \cos {\phi _{2}}\cdot \sin ^{2}\left({\frac {\Delta \lambda }{2}}\right)}}\ ,\\&=2{\sqrt {\left(\sin {\frac {\Delta \lambda }{2}}\cos \phi _{\textrm {m}}\right)^{2}+\left(\cos {\frac {\Delta \lambda }{2}}\sin {\frac {\Delta \phi }{2}}\right)^{2}}}\ ,\end{aligned}}$

where $\phi _{\text{m}}={\tfrac {1}{2}}(\phi _{1}+\phi _{2})$.

Although this formula is accurate for most distances on a sphere, it too suffers from rounding errors for the special (and somewhat unusual) case of antipodal points. A formula that is accurate for all distances is the following special case of the Vincenty formula for an ellipsoid with equal major and minor axes:

${\begin{aligned}\Delta \sigma ={\operatorname {atan2} }{\Bigl (}&{\sqrt {\left(\cos \phi _{2}\sin \Delta \lambda \right)^{2}+\left(\cos \phi _{1}\sin \phi _{2}-\sin \phi _{1}\cos \phi _{2}\cos \Delta \lambda \right)^{2}}},\\&\quad {\sin \phi _{1}\sin \phi _{2}+\cos \phi _{1}\cos \phi _{2}\cos \Delta \lambda }{\Bigr )},\end{aligned}}$

where $\operatorname {atan2} (y,x)$ is the two-argument arctangent. Using atan2 ensures that the correct quadrant is chosen.

 نسخة المتجه

Another representation of similar formulas, but using normal vectors instead of latitude and longitude to describe the positions, is found by means of 3D vector algebra, using the dot product, cross product, or a combination:

${\begin{aligned}\Delta \sigma &=\arccos \left(\mathbf {n} _{1}\cdot \mathbf {n} _{2}\right)\\&=\arcsin \left|\mathbf {n} _{1}\times \mathbf {n} _{2}\right|\\&=\arctan {\frac {\left|\mathbf {n} _{1}\times \mathbf {n} _{2}\right|}{\mathbf {n} _{1}\cdot \mathbf {n} _{2}}}\\\end{aligned}}$

where $\mathbf {n} _{1}$ and $\mathbf {n} _{2}$ are the normals to the sphere at the two positions 1 and 2. Similarly to the equations above based on latitude and longitude, the expression based on arctan is the only one that is well-conditioned for all angles. The expression based on arctan requires the magnitude of the cross product over the dot product.

 من طول القوس

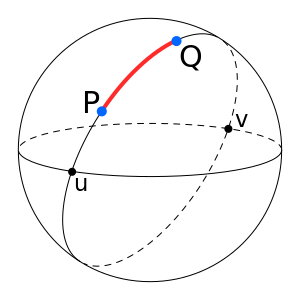
A line through three-dimensional space between points of interest on a spherical Earth is the chord of the great circle between the points. The central angle between the two points can be determined from the chord length. The great circle distance is proportional to the central angle.

The great circle chord length, $\Delta \sigma _{\text{c}}\,\!$, may be calculated as follows for the corresponding unit sphere, by means of Cartesian subtraction:

${\begin{aligned}\Delta {X}&=\cos \phi _{2}\cos \lambda _{2}-\cos \phi _{1}\cos \lambda _{1};\\\Delta {Y}&=\cos \phi _{2}\sin \lambda _{2}-\cos \phi _{1}\sin \lambda _{1};\\\Delta {Z}&=\sin \phi _{2}-\sin \phi _{1};\\\Delta \sigma _{\text{c}}&={\sqrt {(\Delta {X})^{2}+(\Delta {Y})^{2}+(\Delta {Z})^{2}}}.\end{aligned}}$

Substituting $\lambda _{1}=-{\tfrac {1}{2}}\Delta \lambda$ and $\lambda _{2}={\tfrac {1}{2}}\Delta \lambda$ this formula can be algebraically manipulated to the form shown above in § Computational formulae.

 نصف قطر الأرض الكروية

Equatorial (a), polar (b) and mean Earth radii as defined in the 1984 World Geodetic System revision. (Not to scale.)

المقالة الرئيسية: نصف قطر الأرض

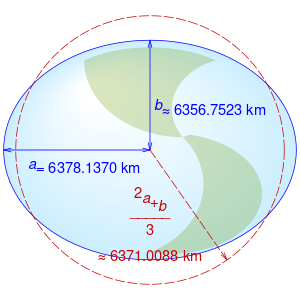
The shape of the Earth closely resembles a flattened sphere (a spheroid) with equatorial radius $a$ of 6378.137 km; distance $b$ from the center of the spheroid to each pole is 6356.7523142 km. When calculating the length of a short north-south line at the equator, the circle that best approximates that line has a radius of ${\textstyle {\frac {b^{2}}{a}}}$ (which equals the meridian's semi-latus rectum), or 6335.439 km, while the spheroid at the poles is best approximated by a sphere of radius ${\textstyle {\frac {a^{2}}{b}}}$, or 6399.594 km, a 1% difference. So long as a spherical Earth is assumed, any single formula for distance on the Earth is only guaranteed correct within 0.5% (though better accuracy is possible if the formula is only intended to apply to a limited area). Using the mean Earth radius, ${\textstyle R_{1}={\frac {1}{3}}(2a+b)\approx 6371.009{\text{ km}}}$ (for the WGS84 ellipsoid) means that in the limit of small flattening, the mean square relative error in the estimates for distance is minimized.

For distances smaller than 500 kilometers and outside of the poles, a Euclidean approximation of an ellipsoidal Earth (Federal Communications Commission's (FCC)'s formula) is both simpler and more accurate (to 0.1%).

 تاريخ

وقد كتب بدرو نونيز الملاح البرتغالي سنة 1537م حول فرص الملاحة في طريق الدائرة الكبرى. ولكن معظم السفن لم تبحر وفقًا لطرق الدائرة الكبرى، حتى أوائل القرن التاسع عشر، عندما تحسنت طرائق الملاحة. وفي أوائل القرن العشرين أصبح طريق الدائرة الكبرى مُصَمَّمًا لأكبر الطرق الجوية.

 انظر أيضاً

• ملاحة جوية
• زاوية مركزية
• Flight planning
• جيوديسيا
• Geographical distance
• ملاحة الدائرة الكبرى
• Haversine formula
• SIGI
• الأرض الكروية
• هندسة كرية
• حساب مثلثات كري
• Versor
• صيغ ڤنسنتي

 المصادر

الموسوعة المعرفية الشاملة

 وصلات خارجية

• GreatCircle at MathWorld
• Global Distance Calculator at Infoplease
• Haversine formula in JavaScript Haversine and other formulae for calculating distances, bearings, etc.