كروي مفلطح
كروي متطاول
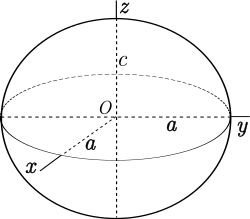
الجسم شبه الكروي (البيضاوي) Spheroid، هو جسم ناتج من تدوير قطع ناقص ( أهليلج ) حول أحد محاوره.
فمثلا البيضة هي من الأجسام شبه الكروية، غير المنتظمة.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
المعادلة The assignment of semi-axes on a spheroid. Ii is oblate if
c<a and prolate if
c>a .
The equation of a tri-axial ellipsoid centred at the origin with semi-axes a ,b , c aligned along the coordinate axes is
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
1
superscript
𝑥
2
superscript
𝑎
2
superscript
𝑦
2
superscript
𝑏
2
superscript
𝑧
2
superscript
𝑐
2
1
{\displaystyle{\displaystyle{\frac{x^{2}}{a^{2}}}+{\frac{y^{2}}{b^{2}}}+{\frac%
{z^{2}}{c^{2}}}=1}}
The equation of a spheroid with Oz as the symmetry axis is given by setting a=b :
x
2
+
y
2
a
2
+
z
2
c
2
=
1
.
superscript
𝑥
2
superscript
𝑦
2
superscript
𝑎
2
superscript
𝑧
2
superscript
𝑐
2
1
{\displaystyle{\displaystyle{\frac{x^{2}+y^{2}}{a^{2}}}+{\frac{z^{2}}{c^{2}}}=%
1.}}
The semi-axis a is the equatorial radius of the spheroid, and c is the distance from centre to pole along the symmetry axis. There are two possible cases:
c < a : oblate spheroid
c > a : prolate spheroid The case of a=c reduces to a sphere.
المساحة An oblate spheroid with c < a has surface area
S
oblate
=
2
π
a
2
(
1
+
1
-
e
2
e
tanh
-
1
e
)
where
e
2
=
1
-
c
2
a
2
.
formulae-sequence
subscript
𝑆
oblate
2
𝜋
superscript
𝑎
2
1
1
superscript
𝑒
2
𝑒
superscript
1
𝑒
where
superscript
𝑒
2
1
superscript
𝑐
2
superscript
𝑎
2
{\displaystyle{\displaystyle S_{\rm{oblate}}=2\pi a^{2}\left(1+{\frac{1-e^{2}}%
{e}}\tanh^{-1}e\right)\quad{\mbox{where}}\quad e^{2}=1-{\frac{c^{2}}{a^{2}}}.}}
The oblate spheroid is generated by rotation about the Oz axis of an ellipse with semi-major axis a and semi-minor axis c , therefore e may be identified as the eccentricity . (See ellipse ). A derivation of this result may be found at.[1]
A prolate spheroid with c > a has surface area
S
prolate
=
2
π
a
2
(
1
+
c
a
e
sin
-
1
e
)
where
e
2
=
1
-
a
2
c
2
.
formulae-sequence
subscript
𝑆
prolate
2
𝜋
superscript
𝑎
2
1
𝑐
𝑎
𝑒
superscript
1
𝑒
where
superscript
𝑒
2
1
superscript
𝑎
2
superscript
𝑐
2
{\displaystyle{\displaystyle S_{\rm{prolate}}=2\pi a^{2}\left(1+{\frac{c}{ae}}%
\sin^{-1}e\right)\qquad{\mbox{where}}\qquad e^{2}=1-{\frac{a^{2}}{c^{2}}}.}}
The prolate spheroid is generated by rotation about the Oz axis of an ellipse with semi-major axis c and semi-minor axis a , therefore e may again be identified as the eccentricity . (See ellipse ). A derivation of this result may be found at.[2]
الحجم The volume inside a spheroid (of any kind) is
(
4
π
/
3
)
a
2
c
≈
4.19
a
2
c
4
𝜋
3
superscript
𝑎
2
𝑐
4.19
superscript
𝑎
2
𝑐
{\displaystyle{\displaystyle(4\pi/3)a^{2}c\approx 4.19\,a^{2}c}}
A =2a is the equatorial diameter, and C =2c is the polar diameter, the volume is
(
π
/
6
)
A
2
C
≈
0.523
A
2
C
𝜋
6
superscript
𝐴
2
𝐶
0.523
superscript
𝐴
2
𝐶
{\displaystyle{\displaystyle(\pi/6)A^{2}C\approx 0.523\,A^{2}C}}
الانحناء If a spheroid is parameterized as
σ
→
(
β
,
λ
)
=
(
a
cos
β
cos
λ
,
a
cos
β
sin
λ
,
c
sin
β
)
;
→
𝜎
𝛽
𝜆
𝑎
𝛽
𝜆
𝑎
𝛽
𝜆
𝑐
𝛽
{\displaystyle{\displaystyle{\vec{\sigma}}(\beta,\lambda)=(a\cos\beta\cos%
\lambda,a\cos\beta\sin\lambda,c\sin\beta);\,\!}}
where
β
𝛽
{\displaystyle{\displaystyle\beta\,\!}}
reduced or parametric latitude
λ
𝜆
{\displaystyle{\displaystyle\lambda\,\!}}
longitude
-
π
2
<
β
<
+
π
2
𝜋
2
𝛽
𝜋
2
{\displaystyle{\displaystyle-{\frac{\pi}{2}}<\beta<+{\frac{\pi}{2}}\,\!}}
-
π
<
λ
<
+
π
𝜋
𝜆
𝜋
{\displaystyle{\displaystyle-\pi<\lambda<+\pi\,\!}}
Gaussian curvature is
K
(
β
,
λ
)
=
c
2
(
a
2
+
(
c
2
-
a
2
)
cos
2
β
)
2
;
𝐾
𝛽
𝜆
superscript
𝑐
2
superscript
superscript
𝑎
2
superscript
𝑐
2
superscript
𝑎
2
superscript
2
𝛽
2
{\displaystyle{\displaystyle K(\beta,\lambda)={c^{2}\over(a^{2}+(c^{2}-a^{2})%
\cos^{2}\beta)^{2}};\,\!}}
and its mean curvature is
H
(
β
,
λ
)
=
c
(
2
a
2
+
(
c
2
-
a
2
)
cos
2
β
)
2
a
(
a
2
+
(
c
2
-
a
2
)
cos
2
β
)
3
/
2
.
𝐻
𝛽
𝜆
𝑐
2
superscript
𝑎
2
superscript
𝑐
2
superscript
𝑎
2
superscript
2
𝛽
2
𝑎
superscript
superscript
𝑎
2
superscript
𝑐
2
superscript
𝑎
2
superscript
2
𝛽
3
2
{\displaystyle{\displaystyle H(\beta,\lambda)={c(2a^{2}+(c^{2}-a^{2})\cos^{2}%
\beta)\over 2a(a^{2}+(c^{2}-a^{2})\cos^{2}\beta)^{3/2}}.\,\!}}
Both of these curvatures are always positive, so that every point on a spheroid is elliptic.
انظر أيضاً الهامش
