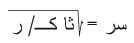الميكانيكا السماوية
| ميكانيكا كلاسيكية | ||||||||
تاريخ...
| ||||||||
الميكانيكا السماوية celestial mechanics هو ذلك الفرع من علم الفلك الذي يدرس الحركات الانسحابية والدورانية والتشوهية للأجرام السماوية، الطبيعي منها والصنعي، نتيجةَ التجاذباتِ التثاقلية المتبادلة بين هذه الأجرام. وكان الفيزيائي الإنكليزي إسحق نيوتن (ع. 1642-1727) أوّلَ من قدم عرضاً رياضيّاً متَّسقاً للميكانيك السماوي عام 1687، مستنداً في عمله إلى قوانينه الثلاثة في الحركة وقانونه في التجاذب التثاقلي الكوني.
وتجدر الإشارة إلى أن الأساس الذي اعتَمد عليه نيوتن في التوصّل إلى نتائجه؛ هو أعمال الفلكي البولوني نيقولا كوپرنيك (ع. 1473-1543)، والفلكي الإيطالي گاليليو گاليلـِيْ (ع. 1564-1642)، والفلكي الدنماركي تيخو براهه Tycho Brahe (ع. 1546-1601)، والفلكي الرياضي الألماني يوهانس كپلر (ع. 1571-1630).
وقد سمحت قوانينُ نيوتن الأربعةُ بصوغ مسائلِ الميكانيك السماويّ (الذي يُسمّى أحياناً الميكانيكَ التثاقليَّ gravitational mechanics) بلغة المعادلات التفاضلية العادية من الدرجة الثانية. وغالباً ما تكون الحسابات التي تُجرى لتعيين حركات الأجرام السماوية جدّ معقدة، لأن هذه الأجرامَ واقعةٌ باستمرار تحت تأثير عدد كبير من القوى المختلفة، إضافةً إلى كونها دائمة الحركة.
كان نيوتن أيضاً أوّل من توصّل إلى حلٍّ كاملٍ لمسألة جسمين two- body problem (أي تعيين حركة جسمين نتيجة تجاذبهما التثاقلي المتبادل، بإهمال القوى الأخرى)، ومن ثَمَّ تمكَّن من تعيين حركاتِ أقمارِ كوكبِ المريخ حوله؛ وحركة القمر حول الأرض، وحركةِ الأرضِ حول الشمس. ولابدّ من الإشارة إلى أن مسألة جسمين هي المسألةُ الوحيدةُ التي حُلّتْ حلاًّ كاملاً في الميكانيك السماوي. و يُعيِّن حلُّ هذه المسألة موقعَ كلٍّ من هذين الجسمين بالنسبة إلى الآخر في أيّ وقتٍ،إضافة إلى تعيين كتلة ِ كلٍّ منهما. بَيْدَ أن مسألة جسمين تفترضُ وجوداً مثاليـاً لهما لا يتحقق في الطبيعة؛ ذلك أنّ ثمة قوى أخرى تؤثر فيهما باستمرار؛ مصدرُها أجسامٌ مادية وظواهرُ فيزيائية أخرى. ومع ذلك، ففي كثير من الحالات (أنظمة النجوم الثنائية مثلاً) توفر مسألةُ جسمين وصفاً لحركتيهما قريباً جدّاً من الواقع. وعندما يكون عددُ الأجسام أكبر من اثنين (الشمس والكواكب في النظام الشمسي، الحشود النجميّة، وغيرها)، تصبحُ مسألة تعيين حركات هذه الأجسام غاية في التعقيد. لذلك يقال غالباً: إنه لا يوجد لمسألة ن من الأجسام n-body problem عندما يكون ن ≤ 3 حلٌّ تحليلــيٌّ كاملٌ، لكنها تُحَلُّ عددياً باستعمال الحواسيب المتطورة، التي توفر للمعادلات التفاضلية للحركة حلولاً عددية قريبةً من الحل الحقيقي لها بأي درجة مطلوبة من الدقة. وتجدر الإشارة إلى أن أستاذ علم الفلك بجامعة كلومبيا الأمريكية والاس إكرت Wallace Eckert كان أول من استعمل الحواسيب بكثافة لحساب مدارات الأجرام السماوية.
تتجلى أبسط حالة لمسألة جسمين في حركة ساتلٍ (قمر) صنعيٍّ في مدارٍ دائريٍّ حول الأرض. في هذه الحالة، تكون الكتلة ك للساتل مهملةً مقارنةً بكتلة الأرض كـ، ومن ثـَمّ يكون تأثيرُه التثاقلي في الأرض مهملاً، وهذا يعني أن من الممكن إهمال التسارع الذي يُحدثه الساتل في الأرض. وفي حركة الساتل الدائرية المنتظمة حول الأرض، تكون قيمة قوة جذب الأرضِ له مساويةً ك سر2/ر حيث سر سرعة الساتل، ر نصف قطر مداره حول الأرض. لكن قوة الجذب هذه تُحَدَّد بقانون نيوتن الرابع، أي بالقيمة ثا ك كـ/ر2، حيث ثا هو ثابت الجاذبية. إذن:
ك سر2/ ر = ثا ك كـ/ر2
ومنه ينتج أن
توفر هذه المساواة البسيطة سرعة أيّ جسمٍ صغير الكتلةِ يدور في مدار دائريٍّ حول جسم آخر كبير الكتلة نسبياً. لكن السرعة الحقيقية للسواتل التي تدور حول الأرض وفق مدارات دائرية تختلف قليلاً عن السرعة المحدَّدة بالمساواة الأخيرة لعدة أسباب من ضمنها الشكلُ غيرُ الكرويِّ للكرة الأرضيّةِ؛ وتوزعُ الكتلة فيها؛ وقوى الجذب التثاقلّيةُ للقمر والشمس؛ والضغطُ الإشعاعيُّ؛ ومقاومةُ الجوِّ الأرضيِّ (عندما يكون مدار الساتلِ قريباً من الأرض). وتسمَّى القوى الناشئة من هذه الأسباب قوى غيرَ مركزيّة non-central forces، ويُحْسَبُ حسابها عادةً بإضافة حدود إلى معادلات حركة جسمين؛ تُسمّى حدوداً اضطرابيَّةً perturbation terms. وتعيَّن هذه الحدود باستعمال نظرية الاضطرابات perturbation theory التي تَدْرُسُ الطرائق الرياضية المستعملة في إيجاد حلِّ مسألةٍ لا يمكن إيجاد حل تام لها؛ وذلك انطلاقـًا من حل مسألة قريبة منها؛ مثل مسألة حركة جسمين.
ولابدّ من الإشارة إلى أن قوانين نيوتن في الحركةِ وقانونه في الجذب العامّ تعجز أحياناً عن تقديم تعليل لبعض الحركات المتعلقة ببعض الأجرام السماوية. وكمثالٍ على ذلك لم تسمح هذه القوانين بتفسير الحركة التقدمية لحضيض كوكب عطارد في مداره حول الشمس. لكن عندما سمحت نظريةُ أينشتاين في النسبيّة العامة بتفسير هذه الحركة وغيرها من المسائل الفلكية - مثال ذلك تحديد مدارات النبّاضات الثنائية binary pulsars - تبيَّن للفلكيين أنه لابد لهم في بعض الحالات من تطبيق نظرية النسبية العامة. ومع ذلك مازال من الممكن حل معظم مسائل الميكانيك السماويِّ حلاَّ مرضياً باستعمال الميكانيك النيوتنيّ التقليدي. وعلى سبيل المثال، لا الحصر، مازال هذا الميكانيك مستعملا ًبنجاح كبير في مسائل السواتل الصنعية؛ إذ تستند المعادلات المستعمـَلة في تحديد حركاتها استناداً كاملاً تقريبـاً إلى طرائق الميكانيك التقليدي.
المصادر
- خضر الأحمد. "الميكانيكُ السَّماويُّ". الموسوعة العربية.
الموضوعات ذات الصلة
- الفلك الكواكب ـ النسبية.
للاستزادة
- خضر الأحمد، أسس الميكانيكا السماوية (عمادة شؤون المكتبات - جامعة الملك سعود، الرياض 1981).
- ألان و. هيرشفيلد، اختلاف المنظر النجمي، ترجمة خضر الأحمد (مكتبة العبيكان، الرياض 2003).
- توماس ت. آرني، استكشافات ومقدمة في علم الفلك، ترجمة أحمد الحصري وسعيد الأسعد ( دار طلاس للدراسات والترجمة والنشر، دمشق 1998).
- H. POLLARD, Mathematical Introduction to Celestial Mechanics (Prentice- Hall, New Jersey,1968). JOHN D. FIX, Astronomy: Journey to the Cosmic Frontier (Mosby 1995).
وصلات خارجية
- Calvert, James B. (2003-03-28), Celestial Mechanics, University of Denver, http://www.du.edu/~jcalvert/phys/orbits.htm, retrieved on 2006-08-21
- Astronomy of the Earth's Motion in Space, high-school level educational web site by David P. Stern
البحث
أعمال فنية
مذكرات دراسية
جمعيات
محاكاة