البعد الرابع

3D projection of a tesseract undergoing a simple rotation

البعد الرابع Fourth dimension عادة يفكر الإنسان في أن أي فراغ له ثلاثة أبعاد: الطول والعرض والارتفاع. فالصندوق الذي طوله ستة أمتار، وعرضه أربعة أمتار، وارتفاعه متران، يمكن وصفه بمجموعة الأرقام (6,4,2). كما يمكن استخدام هذه المجموعة أيضًا لوصف ـ موقع نقطة في الفراغ ـ وليكن مثلاً موقع طائرة. غير أنه لا يمكن تحديد موقع طائرة متحركة بثلاثة أرقام. ولكي نستطيع تحديد موقع طائرة في الجو، بمجموعة الأرقام (6,4,2) مثلاً، فإننا نحتاج إلى بعد رابع هو الزمن.

يمكن لمسار الطائرة التي تطير في الجو أن يُحدَّد في أربعة أبعاد كما في الرسم البياني، وذلك عندما تقلع الطائرة من النقطة (0) وتطير نحو الجنوب الشرقي. فالموضع في المحور (س) يوضح مسافتها جنوب النقطة (0)، كما يوضح الموضع في المحور (ص) مسافتها شرق النقطة (0)، ويوضح الموضع في المحور (ع) ارتفاعها. أما المنحنى (ز) فإنه يمثل مسار الطائرة عبر الفضاء. وتحدد النقاط التي على المنحنى (ز) موضع الطائرة في أربعة أزمان مختلفة تسمى ز (0) إلى ز 4.

وفي أوائل القرن العشرين أدرك عالم الرياضيات هيرمان مِنكوفسكي أن نظرية النسبية التي أطلقها العالم الفيزيائي ألبرت أينشتاين وصفت كونًا ذا أربعة أبعاد. وكما يرى منكوفسكي فإن البعد الزمني يندمج مع الأبعاد المكانية الثلاثة ليشكل الزمان ـ المكان (الزمكان) بعد ذلك بدأ الرياضيون بدراسة أشكال هندسية ذات أربعة أبعاد أو أكثر. نحن نعرف أن في الكون ثلاثة أبعاد: البعد السيني, والبعد الصادي والبعد العيني. ولكن هل هناك أبعاد أكثر من هذه الثلاثة الأبعاد التي ألفناها؟ نحن نعرف أن المتجه إذا كان على صورة < س، ص > فهو متجه ثنائي أبعاد, وإذا كان على صورة < س، ص, ع > فهو متجه ثلاثي أبعاد. والمتجه < س، ص, ع > هو المتجه الذي بدايته نقطة الأصل (0,0,0) ونهايته النقطة (س, ص, ع). لكن ماذا لو أعينا متجها بالصورة < س, ص, ع, ط > وهل البعد ط موجود حقا؟ أم أن الكون مؤلف من فقط ثلاثة أبعاد؟ الجواب: نعم, هناك بعد رابع, ولنسميه ط. وهذا البعد قد يكون زماني وقد يكون مكاني.

  • إذا سلمنا أن البعد الرابع زماني, فإننا نستطيع أن نتخيل الوضع كأنه سلسلة أحداث أو فلم. فإن شكل الجسم في لحظة معينة قد يتغير في اللحظة التي تليها. وهذا البعد الذي تطرق إليه آينشتاين في نظريته النسبية.
  • وقد يكون البعد الرابع الذي نتحدث عنه بعدا مكانيا.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

كيف يمكن أن يكون الربع الرابع مكاني؟ كيف نتخيل الأجسام فيه؟

A net of a tesseract

القطعة المستقيمة عبارة عن مجموعة نقاط مصفوفة على بعد واحد. والأجسام الثنائية الأبعاد كالمثلث والمربع والدائرة تتألف من مجموعة قطع مستقيمة وكل هذه الأجسام تعيش في عالم ثنائي الأبعاد وترى بعضها البعض كخطوط مستقيمة. فهي تألف البعد السيني والصادي وتبرمج عقلها على أن الكون مؤلف من بعدين فقط. وتستطيع التحرك يميناً ويساراً, وشمالاً وجنوباً. لكنها لا تستطيع أن تتحرك, ولا أن تتخيل, الاتجاه الأعلى والأسفل. فتذهب للمدرسة ويشرح له مدرس الهندسة الرياضية, وهو أيضا جسم ثنائي الأبعاد, عن المستقيمات والمتجهات والأجسام ذات البعدين < س، ص > فتألف المادة وتبدع فيها. لكن إذا وصلوا في مادة الهندسة الرياضية إلى المتجه ذي الثلاثة أبعاد < س, ص, ع > فإنه لا يستطيع أن يتخيله ولا يستطيع أن يراه, رغم كونه موجودا. ولا يسعه تخيل الأجسام ذات الثلاثة أبعاد مثل المكعبات والأهرام والكرات, ولا يستطيع أن يراها. والمكعبات والأهرام والكرات عبارة عن أجسام تتكون من عدة شرائح ثنائية الأبعاد.

وإذا زار الجسم الثلاثي الأبعاد العالم الثنائي الأبعاد, فإن الأجسام ثنائية الأبعاد لا تستطيع أن تراه ولا حتى أن تتخيله. وإذا مر جسم ثلاثي أبعاد واخترق المستوي الذي يعيشون فيه فإنهم فقط سيرون شريحة واحدة فقط من الشرائح المكونة له وهي انعكاس الجسم ثلاثي الأبعاد على العالم ثنائي الأبعاد وهذا الانعكاس ثنائي الأبعاد أيضاوتراه الأجسام الأخرى كخط مستقيم.

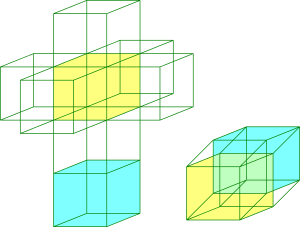
والشيء نفسه ينطبق علينا, نحن أجسام مكونة من ثلاثة أبعاد ونألف الأبعاد الثلاثة السينية والصادية والعينية. ونرى انعكاسات الأجسام الثلاثية الأبعاد والتي هي ثنائية أبعاد. ولكننا لا نألف بعداً رابعاً. ولا نستطيع أن نتخيل الأجسام ذات الأربعة أبعاد لكننا نستطيع أن نرى انعكاسها على عالمنا الثلاثي الأبعاد. وكما أن العالم الثلاثي الأبعاد عبارة عن مجموعة عوالم ثنائية الأبعاد (مستويات) متراصة فوق بعضها البعض, فإن العالم الرباعي الأبعاد عبارة عن مجموعة عوالم ثلاثية الأبعاد فوق وجنب وخلف بعضها البعض. وهذه أشكال انعكاسات جسيم الرباعي الأبعاد في العالم ثلاثي الأبعاد.


إثبات وجود البعد الرابع

الحديث عن مفهوم البعد الرابع إنما هو فلسفات, وإن كانت منطقية. ولا يوجد أي إسناد علمي أو معادلات رياضية جبرية تؤيد مفهوم البعد الرابع.

لكن نظرية الأوتار, التي تقول أن المادة مكونة من أوتار صغيرة من الطاقة, والتي تعتبر القوى الكهرومغناطيسية والجاذبية كقوى واحدة, تنطوي على وجود أحد عشر بعداً (البعد السيني والبعد الصادي والبعد العيني إضافة إلى الزمن وسبعة أبعاد أخرى). هذه النظرية لا زالت في تحت التطوير ولم تثبت بعد.

نظرية الأوتار تقول أن عالمنا المكون من ثلاثة أبعاد متجاور مع عوالم مشابهة أخرى وهذا ما يكون البعد الرابع, كما أنا عالمنا ثلاثي الأبعاد يتكون من عوالم لا نهائية ثنائية الأبعاد.

يأمل القائمون على نظرية الأوتار أن يتوصل تقدم العلم إلى إثبات النظرية. تثبت النظرية عن طريق تسريع جزيئين صغيرين (بروتونين) وعند تصادمهما ببعضهما سينتج عن هذا الاصطدام جزيئات أصغر من ضمنها الجسيم الافتراضي الذي أطلق عليه اسم غرافيتون, Graviton. الغرافيتون عبارة عن جسيم افتراضي يتأثر بالجاذبية وله خاصية وهو التنقل بين العوالم ثلاثية الأبعاد. فإذا اصطدم بروتونين ونتج عن الاصطدام خروج الغرافيتون فإن ذلك سوف يثبت وجود البعد الرابع.

التوقعات

Cube Tesseract Description
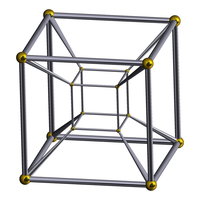
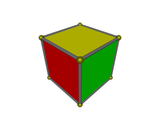
Cube-face-first.png Tesseract-perspective-cell-first.png The image on the left is a cube viewed face-on. The analogous viewpoint of the tesseract in 4 dimensions is the cell-first perspective projection, shown on the right. One may draw an analogy between the two: just as the cube projects to a square, the tesseract projects to a cube.

Note that the other 5 faces of the cube are not seen here. They are obscured by the visible face. Similarly, the other 7 cells of the tesseract are not seen here because they are obscured by the visible cell.

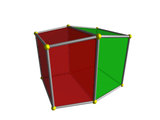
Cube-edge-first.png Tesseract-perspective-face-first.png The image on the left shows the same cube viewed edge-on. The analogous viewpoint of a tesseract is the face-first perspective projection, shown on the right. Just as the edge-first projection of the cube consists of two trapezoids, the face-first projection of the tesseract consists of two frustums.

The nearest edge of the cube in this viewpoint is the one lying between the red and green faces. Likewise, the nearest face of the tesseract is the one lying between the red and green cells.

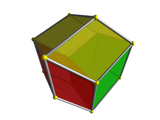
Cube-vertex-first.png Tesseract-perspective-edge-first.png On the left is the cube viewed corner-first. This is analogous to the edge-first perspective projection of the tesseract, shown on the right. Just as the cube's vertex-first projection consists of 3 deltoids surrounding a vertex, the tesseract's edge-first projection consists of 3 hexahedral volumes surrounding an edge. Just as the nearest vertex of the cube is the one where the three faces meet, so the nearest edge of the tesseract is the one in the center of the projection volume, where the three cells meet.
Cube-edge-first.png Tesseract-perspective-edge-first.png A different analogy may be drawn between the edge-first projection of the tesseract and the edge-first projection of the cube. The cube's edge-first projection has two trapezoids surrounding an edge, while the tesseract has three hexahedral volumes surrounding an edge.
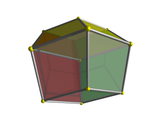
Cube-vertex-first.png Tesseract-perspective-vertex-first.png On the left is the cube viewed corner-first. The vertex-first perspective projection of the tesseract is shown on the right. The cube's vertex-first projection has three tetragons surrounding a vertex, but the tesseract's vertex-first projection has four hexahedral volumes surrounding a vertex. Just as the nearest corner of the cube is the one lying at the center of the image, so the nearest vertex of the tesseract lies not on boundary of the projected volume, but at its center inside, where all four cells meet.

Note that only three faces of the cube's 6 faces can be seen here, because the other 3 lie behind these three faces, on the opposite side of the cube. Similarly, only 4 of the tesseract's 8 cells can be seen here; the remaining 4 lie behind these 4 in the fourth direction, on the far side of the tesseract.

الظلال

Schlegel wireframe 8-cell.png


انظر ايضا

 هناك كتاب ، Special Relativity، في معرفة الكتب.
اقرأ نصاً ذا علاقة في

Flatland


المصادر

وصلات خارجية

تمّ الاسترجاع من "https://www.marefa.org/w/index.php?title=البعد_الرابع&oldid=4002265"