متوسط متحرك
في الاحصاء، المتوسط المتحرك، ويسمى أيضا المتوسط المتداول، المعنى المتداول، أو المتوسط الجاري، هو نوع من finite impulse response filter تستخدم لتحليل مجموعة من نقاط البيانات عن طريق تكوين سلاسل من متوسطات مختلفة والتي تعتبر مجموعات فرعية من البيانات الكاملة ذاتها.
التعريف
يتم استخدام المتوسط المتحرك من قبل المهندسين الصناعيين بفعالة للتنبؤ بقدر كمية الطلب على منتج من منتجات المصنع، ويتم تقدير كمية الطب بحساب المتوسط عن طريق جمع كميات الطلب في الاشهر او السنوات السابقة ثم قسمة المجموع على عدد الاشهر او السنوات. وسمي بالمتحرك لأن البيانات في هذه الحسابات "تتحرك" تدريجيا على مر الزمن، أي ان بيانات كميات الطلب الحديثة فقط تدخل في حساب المتوسط.
الطلب ثابت
المتوسط المتحرك لا يتفاعل مع الزيادات المضطردة في الطلب، لذا لا ينطبق المتوسط المتحرك إلا عندما تكون كميات الطلب مستقرة بشكل عام.
عيوب المتوسط المتحرك
على الرغم من ان هذا النوع من طرق التنبؤ شائع بين المهندسين الصناعيين إلا انه لا يخلو من العيوب التي قد تنقص من دقته في التنبؤ لكميات الطلب. من أبرز عيوب المتوسط المتحرك انه يعطي كل قيمة من قيم الطلب التاريخية وزن نسبي مساوي لجميع القيم الاخرى بغض النظر عن المكان الفعلي او التأثير الحقيقي لتلك القيمة. في هذه الحالة يكون التنبؤ قد فقد تاثير القيمة الجديدة التي غالبا ما تكون أهم من القيم السابقة.
طريقة الحساب
لنفرض أنه لدينا عدد من القيم يرمز لكل واحدة منها بــ سك القيمة الاولى = س1 و القيمة الثانية = س2 و القيمة الثالثة = س3 .... و هكذا و عدد هذه القيم هو ن فيكون المتوسط المتحرك البسيط كما يلي:
(م) = ( س1 + س2+ س3+ .......... + س ن ) ÷ ن
مثال:
يقوم مصنع بإنتاج بطاريات للشاحنات و كان حجم الطلب للثلاثة الأشهر السابقة للبطاريات كما يلي:
| الشهر | الطلب (بطارية) |
|---|---|
| الأول | 66 |
| الثاني | 70 |
| الثالث | 68 |
اذا اردنا ان نتنبأ بالطلب للشهر الرابع من هذه البطاريات فاننا نقوم بتطبيق المعادلة السابقة كما يلي:
س1= 66 و س2 = 70 و س3 = 68
فيكون لدينا ثلاث قيم , ن = 3
لهذا :
م = ( 66+ 70+ 68) ÷ 3 = 68 بطارية
لذا فان الطلب المتوقع للشهر الرابع هو 68 بطارية.
المتوسط المتحرك البسيط
A simple moving average (SMA) is the unweighted mean of the previous n data points.[citation needed] For example, a 10-day simple moving average of closing price is the mean of the previous 10 days' closing prices. If those prices are then the formula is
When calculating successive values, a new value comes into the sum and an old value drops out, meaning a full summation each time is unnecessary,
In technical analysis there are various popular values for n, like 10 days, 40 days, or 200 days. The period selected depends on the kind of movement one is concentrating on, such as short, intermediate, or long term. In any case moving average levels are interpreted as support in a rising market, or resistance in a falling market.
In all cases a moving average lags behind the latest data point, simply from the nature of its smoothing. An SMA can lag to an undesirable extent, and can be disproportionately influenced by old data points dropping out of the average. This is addressed by giving extra weight to more recent data points, as in the weighted and exponential moving averages.
One characteristic of the SMA is that if the data have a periodic fluctuation, then applying an SMA of that period will eliminate that variation (the average always containing one complete cycle). But a perfectly regular cycle is rarely encountered in economics or finance.[1]
For a number of applications it is advantageous to avoid the shifting induced by using only 'past' data. Hence a central moving average can be computed, using both 'past' and 'future' data. The 'future' data in this case are not predictions, but merely data obtained after the time at which the average is to be computed.
المتوسط المتحرك التراكمي
The cumulative moving average[citation needed] is also frequently called a running average or a long running average[citation needed] although the term running average is also used as synonym for a moving average.[citation needed] This article uses the term cumulative moving average or simply cumulative average since this term is more descriptive and unambiguous.
In some data acquisition systems, the data arrives in an ordered data stream and the statistician would like to get the average of all of the data up until the current data point. For example, an investor may want the average price of all of the stock transactions for a particular stock up until the current time. As each new transaction occurs, the average price at the time of the transaction can be calculated for all of the transactions up to that point using the cumulative average. This is the cumulative average, which is typically an unweighted average of the sequence of i values x1, ..., xi up to the current time:
The brute force method to calculate this would be to store all of the data and calculate the sum and divide by the number of data points every time a new data point arrived. However, it is possible to simply update cumulative average as a new value xi+1 becomes available, using the formula:[citation needed]
where CA0 can be taken to be equal to 0.
Thus the current cumulative average for a new data point is equal to the previous cumulative average plus the difference between the latest data point and the previous average divided by the number of points received so far. When all of the data points arrive (i = N), the cumulative average will equal the final average.
The derivation of the cumulative average formula is straightforward. Using
and similarly for i + 1, it is seen that
Solving this equation for CAi+1 results in:
Weighted moving average
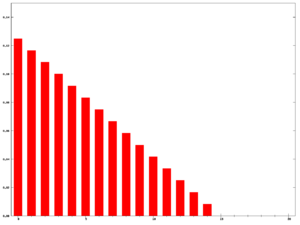
A weighted average is any average that has multiplying factors to give different weights to different data points. Mathematically, the moving average is the convolution of the data points with a moving average function;[citation needed] in technical analysis, a weighted moving average (WMA) has the specific meaning of weights that decrease arithmetically.[citation needed] In an n-day WMA the latest day has weight n, the second latest n − 1, etc, down to zero.
The denominator is a triangle number, and can be easily computed as
When calculating the WMA across successive values, it can be noted the difference between the numerators of WMAM+1 and WMAM is npM+1 − pM − ... − pM−n+1. If we denote the sum pM + ... + pM−n+1 by TotalM, then
The graph at the right shows how the weights decrease, from highest weight for the most recent data points, down to zero. It can be compared to the weights in the exponential moving average which follows.
المتوسط المتحرك الأسي
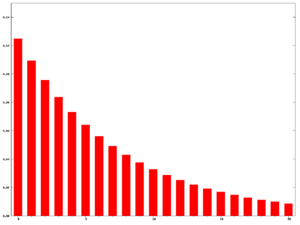
An exponential moving average (EMA), sometimes also called an exponentially weighted moving average (EWMA),[citation needed] applies weighting factors which decrease exponentially. The weighting for each older data point decreases exponentially, giving much more importance to recent observations while still not discarding older observations entirely. The graph at right shows an example of the weight decrease.
Parameters:
- The degree of weighting decrease is expressed as a constant smoothing factor α, a number between 0 and 1. The smoothing factor may be expressed as a percentage, so a value of 10% is equivalent to α = 0.1. A higher α discounts older observations faster. Alternatively, α may be expressed in terms of N time periods, where α = 2/(N+1). For example, N = 19 is equivalent to α = 0.1. The half-life of the weights (the interval over which the weights decrease by a factor of two) is approximately N/2.8854 (within 1% if N > 5).
- The observation at a time period t is designated Yt, and the value of the EMA at any time period t is designated St.
S1 is undefined. S2 may be initialized in a number of different ways, most commonly by setting S2 to Y1, though other techniques exist, such as setting S2 to an average of the first 4 or 5 observations. The prominence of the S2 initialization's effect on the resultant moving average depends on α; smaller α values make the choice of S2 relatively more important than larger α values, since a higher α discounts older observations faster.
Formula:
The formula for calculating the EMA at time periods t > 2 is
This formulation is according to Hunter (1986)[2]. By repeated application of this formula for different times, we can eventually write St as a weighted sum of the data points Yt, thus:
for any suitable k = 0, 1, 2, ... The weight of the general data point is .
An alternate approach by Roberts (1959) uses Yt in lieu of Yt−1[3]:
This formula can also be expressed in technical analysis terms as follows, showing how the EMA steps towards the latest data point, but only by a proportion of the difference (each time):[4]
Expanding out each time results in the following power series, showing how the weighting factor on each data point p1, p2, etc, decreases exponentially:
This is an infinite sum with decreasing terms.
The N periods in an N-day EMA only specify the α factor. N is not a stopping point for the calculation in the way it is in an SMA or WMA. For sufficiently large N, The first N data points in an EMA represent about 86% of the total weight in the calculation[6]:
- i.e. simplified[7], tends to .
The power formula above gives a starting value for a particular day, after which the successive days formula shown first can be applied. The question of how far back to go for an initial value depends, in the worst case, on the data. If there are huge p price values in old data then they'll have an effect on the total even if their weighting is very small. If one assumes prices don't vary too wildly then just the weighting can be considered. The weight omitted by stopping after k terms is
which is
i.e. a fraction
out of the total weight.
For example, to have 99.9% of the weight,
terms should be used. Since approaches as N increases[8], this simplifies to approximately[9]
for this example (99.9% weight).
المتوسط المتحرك المعدل
This is called modified moving average (MMA), running moving average (RMA), or smoothed moving average.
Definition
In short, this is exponential moving average, with .
Application to measuring computer performance
Some computer performance metrics, e.g. the average process queue length, or the average CPU utilization, use a form of exponential moving average.
Here is defined as a function of time between two readings. An example of a coefficient giving bigger weight to the current reading, and smaller weight to the older readings is
where time for readings tn is expressed in seconds, and is the period of time in minutes over which the reading is said to be averaged (the mean lifetime of each reading in the average). Given the above definition of , the moving average can be expressed as
For example, a 15-minute average L of a process queue length Q, measured every 5 seconds (time difference is 5 seconds), is computed as
Other weightings
Other weighting systems are used occasionally - for example, in share trading a volume weighting will weight each time period in proportion to its trading volume.
A further weighting, used by actuaries, is Spencer's 15-Point Moving Average[10] (a central moving average). The symmetric weight coefficients are -3, -6, -5, 3, 21, 46, 67, 74, 67, 46, 21, 3, -5, -6, -3.
المتوسط المتحرك
From a statistical point of view, the moving average, when used to estimate the underlying trend in a time series, is susceptible to rare events such as rapid shocks or other anomalies. A more robust estimate of the trend is the simple moving median over n time points:
where the median is found by, for example, sorting the values inside the brackets and finding the value in the middle.
Statistically, the moving average is optimal for recovering the underlying trend of the time series when the fluctuations about the trend are normally distributed. However, the normal distribution does not place high probability on very large deviations from the trend which explains why such deviations will have a disproportionately large effect on the trend estimate. It can be shown that if the fluctuations are instead assumed to be Laplace distributed, then the moving median is statistically optimal[11]. For a given variance, the Laplace distribution places higher probability on rare events than does the normal, which explains why the moving median tolerates shocks better than the moving mean.
When the simple moving median above is central, the smoothing is identical to the median filter which has applications in, for example, image signal processing.
انظر أيضا
المصادر
- كتاب: production and operations analysis للدكتور Steven Nahmias
- كتاب: ادارة الانتاج و العمليات للدكتور محمد توفيق ماضي
- كتاب: طرق التنبؤ الاحصائي للدكتور عدنان ماجد بري
الهوامش والمصادر
- ^ Statistical Analysis, Ya-lun Chou, Holt International, 1975, ISBN 0030894220, section 17.9.
- ^ NIST/SEMATECH e-Handbook of Statistical Methods: Single Exponential Smoothing at the National Institute of Standards and Technology
- ^ NIST/SEMATECH e-Handbook of Statistical Methods: EWMA Control Charts at the National Institute of Standards and Technology
- ^ Moving Averages page at StockCharts.com
- ^ , since .
- ^ The denominator on the left-hand side should be unity, and the numerator will become the right-hand side (geometric series), .
- ^ Because (1+x/n)n becomes ex for large n.
- ^ It means -> 0, and the Taylor series of tends to .
- ^ loge(0.001) / 2 = -3.45
- ^ Spencer's 15-Point Moving Average — from Wolfram MathWorld
- ^ G.R. Arce, "Nonlinear Signal Processing: A Statistical Approach", Wiley:New Jersey, USA, 2005.






















![{\displaystyle \lim _{N\to \infty }\left[1-{\left(1-{2 \over N+1}\right)}^{N+1}\right]}](https://www.marefa.org/api/rest_v1/media/math/render/svg/530a883020214767d5958af035e1c0c54308f07f)





















