تطبيق خطي

في الرياضيات، التطبيق الخطي linear map (المسمى أيضاً التعيين الخطي، أو التحويل الخطي، أو تشاكل فضاء متجه، أو في بعض السياقات دالة خطية) هي تعيين خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V \to W} بين فضائين متجهين للحفاظ على عمليات إضافة المتجهات و الضرب العددي. يتم استخدام نفس الأسماء ونفس التعريف أيضاً للحالة الأكثر عمومية لـ الوحدات على الحلقات؛ انظر تشاكل وحدة.

إذا كان التطبيق الخطي عبارة عن تقابل فإنها تسمى تساوي الشكل. في الحالة التي يكون فيها $V=W$ ، يسمى التطبيق الخطي (خطياً) إندومورفية. أحياناً يشير المصطلح العامل الخطي إلى هذه الحالة،^[1] ولكن يمكن أن يكون لمصطلح "العامل الخطي" معانٍ مختلفة لمصطلحات مختلفة: على سبيل المثال، يمكن استخدامه للتأكيد على أن $V$ و $W$ هما مسافات متجهة حقيقية (ليس بالضرورة مع $V=W$ ),^{[بحاجة لمصدر]} أو يمكن استخدامها للتأكيد على أن خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} هو فضاء دالة، وهو اصطلاح شائع في التحليل الدالي.^[2]أحيانًا يكون للمصطلح نظم خطية نفس معنى التطبيق الخطي، بينما في التحليل ليس كذلك.

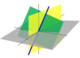
تطبيق خطي من V إلى W دائماً تعين أصل V إلى أصل W. علاوة على ذلك، فإنه يقوم بتعيين فضاء خطي جزئي في V على فضاءات فرعية خطية في W (ربما ذات بعد أقل);^[3]على سبيل المثال، تقوم بتعيين المستوى من خلال الأصل في V إلى إما مستوى من خلال الأصل في W، و خط من خلال الأصل في W، أو مجرد الأصل في W. غالباً ما يمكن تمثيل التطبيق الخطي على أنه مصفوفات، وتشمل الأمثلة البسيطة الدوران والانعكاس في التحويلات الخطية.

في لغة نظرية التصنيفات، التطبيق الخطي هو انحفاظ الشكل في الفضاءات المتجهة.

Definition and first consequences

Let خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} be vector spaces over the same field خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} . A function خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f: V \to W} is said to be a linear map if for any two vectors خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf{u}, \mathbf{v} \in V} and any scalar خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle c \in K} the following two conditions are satisfied:

Additivity / operation of addition: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\mathbf{u}+\mathbf{v}) = f(\mathbf{u})+f(\mathbf{v})}
Homogeneity of degree 1 / operation of scalar multiplication: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(c \mathbf{u}) = c f(\mathbf{u})}

Thus, a linear map is said to be operation preserving. In other words, it does not matter whether the linear map is applied before (the right hand sides of the above examples) or after (the left hand sides of the examples) the operations of addition and scalar multiplication.

By the associativity of the addition operation denoted as +, for any vectors خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf{u}_1, \ldots, \mathbf{u}_n \in V} and scalars خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle c_1, \ldots, c_n \in K,} the following equality holds:^[4]^[5] خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(c_1 \mathbf{u}_1 + \cdots + c_n \mathbf{u}_n) = c_1 f(\mathbf{u}_1) + \cdots + c_n f(\mathbf{u}_n).}

Denoting the zero elements of the vector spaces خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} by خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf{0}_V} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf{0}_W} respectively, it follows that خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f(\mathbf{0}_V) = \mathbf{0}_W.} Let خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle c = 0} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf{v} \in V} in the equation for homogeneity of degree 1: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\mathbf{0}_V) = f(0\mathbf{v}) = 0f(\mathbf{v}) = \mathbf{0}_W.}

Occasionally, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} can be vector spaces over different fields. It is then necessary to specify which of these ground fields is being used in the definition of "linear". If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} are spaces over the same field خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} as above, then we talk about خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} -linear maps. For example, the conjugation of complex numbers is an خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R} -linear map خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Complex \to \Complex} , but it is not خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Complex} -linear, where خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Complex} are symbols representing the sets of real numbers and complex numbers, respectively.

A linear map خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V \to K} with خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} viewed as a one-dimensional vector space over itself is called a linear functional.^[6]

These statements generalize to any left-module خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle {}_R M} over a ring خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} without modification, and to any right-module upon reversing of the scalar multiplication.

Examples

A prototypical example that gives linear maps their name is a function خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f: \mathbb{R} \to \mathbb{R}: x \mapsto cx} , of which the graph is a line through the origin.^[7]
More generally, any homothety خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf{v} \mapsto c\mathbf{v}} where خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} centered in the origin of a vector space is a linear map.
The zero map خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf x \mapsto \mathbf 0} between two vector spaces (over the same field) is linear.
The identity map on any module is a linear operator.
For real numbers, the map خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle x \mapsto x^2} is not linear.
For real numbers, the map خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle x \mapsto x + 1} is not linear (but is an affine transformation).
If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is a خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m \times n} real matrix, then خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} defines a linear map from خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R^n} to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R^m} by sending a column vector خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf x \in \R^n} to the column vector خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \mathbf x \in \R^m} . Conversely, any linear map between finite-dimensional vector spaces can be represented in this manner; see the § Matrices, below.
If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f: V \to W} is an isometry between real normed spaces such that خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f(0) = 0} then خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} is a linear map. This result is not necessarily true for complex normed space.^[8]
Differentiation defines a linear map from the space of all differentiable functions to the space of all functions. It also defines a linear operator on the space of all smooth functions (a linear operator is a linear endomorphism, that is a linear map where the domain and codomain of it is the same). An example is خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d}{dx} \left( c_1 f_1(x) + c_2 f_2(x) + \cdots + c_n f_n(x) \right) = c_1 \frac{d f_1(x)}{dx} + c_2 \frac{d f_2( x)}{dx} + \cdots + c_n \frac{d f_n(x)}{dx}.}
A definite integral over some interval $I$ is a linear map from the space of all real-valued integrable functions on $I$ to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R} . For example, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_a^b {\left[c_1 f_1(x) + c_2 f_2(x) + \dots + c_n f_n(x)\right] dx} = {c_1 \int_a^b f_1(x) \, dx} + {c_2 \int_a^b f_2(x) \, dx} + \cdots + {c_n \int_a^b f_n(x) \, dx}. }
An indefinite integral (or antiderivative) with a fixed integration starting point defines a linear map from the space of all real-valued integrable functions on خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R} to the space of all real-valued, differentiable functions on خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R} . Without a fixed starting point, the antiderivative maps to the quotient space of the differentiable functions by the linear space of constant functions.
If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} are finite-dimensional vector spaces over a field $F$ , of respective dimensions $m$ and $n$ , then the function that maps linear maps خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f: V \to W} to $n \times m$ matrices in the way described in § Matrices (below) is a linear map, and even a linear isomorphism.
The expected value of a random variable (which is in fact a function, and as such a element of a vector space) is linear, as for random variables خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} we have خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle E[X + Y] = E[X] + E[Y]} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle E[aX] = aE[X]} , but the variance of a random variable is not linear.

The function خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f:\R^2 \to \R^2} with خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f(x, y) = (2x, y)} is a linear map. This function scales the خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle x} component of a vector by the factor خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle 2} .
The function خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f(x, y) = (2x, y)} is additive: It doesn't matter whether vectors are first added and then mapped or whether they are mapped and finally added: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f(\mathbf a + \mathbf b) = f(\mathbf a) + f(\mathbf b)}
The function خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f(x, y) = (2x, y)} is homogeneous: It doesn't matter whether a vector is first scaled and then mapped or first mapped and then scaled: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f(\lambda \mathbf a) = \lambda f(\mathbf a)}

Matrices

If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} are finite-dimensional vector spaces and a basis is defined for each vector space, then every linear map from خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} can be represented by a matrix.^[9] This is useful because it allows concrete calculations. Matrices yield examples of linear maps: if خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is a real خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m \times n} matrix, then خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\mathbf x) = A \mathbf x} describes a linear map خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R^n \to \R^m} (see Euclidean space).

Let خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ \bold{v}_1, \ldots , \bold{v}_n \}} be a basis for خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} . Then every vector خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{v} \in V} is uniquely determined by the coefficients خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{c}_1, \ldots , \bold{c}_n} in the field خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R^n} : خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_1 \mathbf{v}_1 + \cdots + c_n \mathbf{v}_n.}

If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f: V \to W} is a linear map, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f\left(c_1 \mathbf{v}_1 + \cdots + c_n \mathbf{v}_n\right) = c_1 f\left(\mathbf{v}_1\right) + \cdots + c_n f\left(\mathbf{v}_n\right),}

which implies that the function f is entirely determined by the vectors خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\bold{v}_1), \ldots , f(\bold{v}_n)} . Now let خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ \bold{w}_1, \ldots , \bold{w}_m \}} be a basis for خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} . Then we can represent each vector خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\bold{v}_j)} as خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f\left(\mathbf{v}_j\right) = a_{1j} \mathbf{w}_1 + \cdots + a_{mj} \mathbf{w}_m.}

Thus, the function خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} is entirely determined by the values of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{ij}} . If we put these values into an خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m \times n} matrix خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} , then we can conveniently use it to compute the vector output of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} for any vector in خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} . To get خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} , every column خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} is a vector خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} a_{1j} \\ \vdots \\ a_{mj} \end{pmatrix}} corresponding to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\bold{v}_j)} as defined above. To define it more clearly, for some column خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} that corresponds to the mapping خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\bold{v}_j)} , خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{M} = \begin{pmatrix} \ \cdots & a_{1j} & \cdots\ \\ & \vdots & \\ & a_{mj} & \end{pmatrix}} where خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} is the matrix of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} . In other words, every column خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = 1, \ldots, n} has a corresponding vector خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\bold{v}_j)} whose coordinates خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{1j} + \cdots + a_{mj}} are the elements of column خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} . A single linear map may be represented by many matrices. This is because the values of the elements of a matrix depend on the bases chosen.

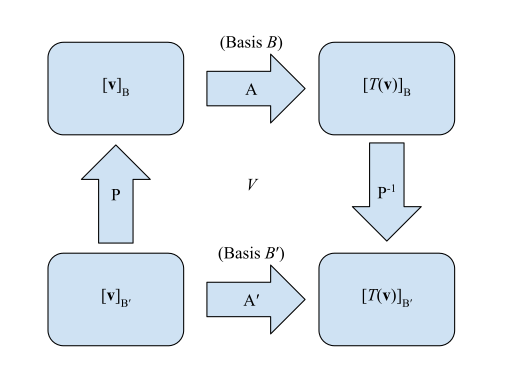
The matrices of a linear transformation can be represented visually:

Matrix for خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle T} relative to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle B} : خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A}
Matrix for خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle T} relative to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle B'} : خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A'}
Transition matrix from خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle B'} to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle B} : خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle P}
Transition matrix from خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle B} to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle B'} : خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle P^{-1}}

The relationship between matrices in a linear transformation

Such that starting in the bottom left corner خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[\mathbf{v}\right]_{B'}} and looking for the bottom right corner خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[T\left(\mathbf{v}\right)\right]_{B'}} , one would left-multiply—that is, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A'\left[\mathbf{v}\right]_{B'} = \left[T\left(\mathbf{v}\right)\right]_{B'}} . The equivalent method would be the "longer" method going clockwise from the same point such that خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[\mathbf{v}\right]_{B'}} is left-multiplied with خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle P^{-1}AP} , or خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle P^{-1}AP\left[\mathbf{v}\right]_{B'} = \left[T\left(\mathbf{v}\right)\right]_{B'}} .

Examples in two dimensions

In two-dimensional space R² linear maps are described by 2 × 2 matrices. These are some examples:

rotation
- by 90 degrees counterclockwise: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A} = \begin{pmatrix} 0 & -1\\ 1 & 0\end{pmatrix}}
- by an angle θ counterclockwise: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A} = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}}
reflection
- through the x axis: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A} = \begin{pmatrix} 1 & 0\\ 0 & -1\end{pmatrix}}
- through the y axis: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A} = \begin{pmatrix}-1 & 0\\ 0 & 1\end{pmatrix}}
- through a line making an angle θ with the origin: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A} = \begin{pmatrix}\cos{2 \theta} & \sin{2 \theta} \\ \sin{2 \theta} & -\cos{2 \theta} \end{pmatrix}}
scaling by 2 in all directions: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A} = \begin{pmatrix} 2 & 0\\ 0 & 2\end{pmatrix} = 2\mathbf{I}}
horizontal shear mapping: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A} = \begin{pmatrix} 1 & m\\ 0 & 1\end{pmatrix}}
squeeze mapping: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A} = \begin{pmatrix} k & 0\\ 0 & \frac{1}{k}\end{pmatrix}}
projection onto the y axis: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A} = \begin{pmatrix} 0 & 0\\ 0 & 1\end{pmatrix}.}

Vector space of linear maps

The composition of linear maps is linear: if خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f: V \to W} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle g: W \to Z} are linear, then so is their composition خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle g \circ f: V \to Z} . It follows from this that the class of all vector spaces over a given field K, together with K-linear maps as morphisms, forms a category.

The inverse of a linear map, when defined, is again a linear map.

If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f_1: V \to W} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f_2: V \to W} are linear, then so is their pointwise sum خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1 + f_2} , which is defined by خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (f_1 + f_2)(\mathbf x) = f_1(\mathbf x) + f_2(\mathbf x)} .

If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f: V \to W} is linear and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha} is an element of the ground field خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle K} , then the map خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha f} , defined by خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle (\alpha f)(\mathbf x) = \alpha (f(\mathbf x))} , is also linear.

Thus the set خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathcal{L}(V, W)} of linear maps from خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V} to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle W} itself forms a vector space over خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle K} ,^[10] sometimes denoted خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{Hom}(V, W)} .^[11] Furthermore, in the case that خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V = W} , this vector space, denoted خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{End}(V)} , is an associative algebra under composition of maps, since the composition of two linear maps is again a linear map, and the composition of maps is always associative. This case is discussed in more detail below.

Given again the finite-dimensional case, if bases have been chosen, then the composition of linear maps corresponds to the matrix multiplication, the addition of linear maps corresponds to the matrix addition, and the multiplication of linear maps with scalars corresponds to the multiplication of matrices with scalars.

Endomorphisms and automorphisms

A linear transformation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f: V \to V} is an endomorphism of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V} ; the set of all such endomorphisms خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{End}(V)} together with addition, composition and scalar multiplication as defined above forms an associative algebra with identity element over the field خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle K} (and in particular a ring). The multiplicative identity element of this algebra is the identity map خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{id}: V \to V} .

An endomorphism of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V} that is also an isomorphism is called an automorphism of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V} . The composition of two automorphisms is again an automorphism, and the set of all automorphisms of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V} forms a group, the automorphism group of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V} which is denoted by خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{Aut}(V)} or خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{GL}(V)} . Since the automorphisms are precisely those endomorphisms which possess inverses under composition, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{Aut}(V)} is the group of units in the ring خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{End}(V)} .

If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V} has finite dimension خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle n} , then خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{End}(V)} is isomorphic to the associative algebra of all خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle n \times n} matrices with entries in خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle K} . The automorphism group of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V} is isomorphic to the general linear group خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{GL}(n, K)} of all خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle n \times n} invertible matrices with entries in خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle K} .

Kernel, image and the rank–nullity theorem

If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f: V \to W} is linear, we define the kernel and the image or range of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f} by خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \ker(f) &= \{\,\mathbf x \in V: f(\mathbf x) = \mathbf 0\,\} \\ \operatorname{im}(f) &= \{\,\mathbf w \in W: \mathbf w = f(\mathbf x), \mathbf x \in V\,\} \end{align}}

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \ker(f)} is a subspace of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{im}(f)} is a subspace of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle W} . The following dimension formula is known as the rank–nullity theorem:^[12] خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim(\ker( f )) + \dim(\operatorname{im}( f )) = \dim( V ).}

The number خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \dim(\operatorname{im}(f))} is also called the rank of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f} and written as خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{rank}(f)} , or sometimes, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \rho(f)} ;^[13]^[14] the number خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \dim(\ker(f))} is called the nullity of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f} and written as خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \operatorname{null}(f)} or خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \nu(f)} .^[13]^[14] If خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle V} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle W} are finite-dimensional, bases have been chosen and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f} is represented by the matrix خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A} , then the rank and nullity of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f} are equal to the rank and nullity of the matrix خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A} , respectively.

Cokernel

A subtler invariant of a linear transformation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle f: V \to W} is the cokernel, which is defined as خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{coker}(f) := W/f(V) = W/\operatorname{im}(f).}

This is the dual notion to the kernel: just as the kernel is a subspace of the domain, the co-kernel is a quotient space of the target. Formally, one has the exact sequence خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \to \ker(f) \to V \to W \to \operatorname{coker}(f) \to 0.}

These can be interpreted thus: given a linear equation f(v) = w to solve,

the kernel is the space of solutions to the homogeneous equation f(v) = 0, and its dimension is the number of degrees of freedom in the space of solutions, if it is not empty;
the co-kernel is the space of constraints that the solutions must satisfy, and its dimension is the maximal number of independent constraints.

The dimension of the co-kernel and the dimension of the image (the rank) add up to the dimension of the target space. For finite dimensions, this means that the dimension of the quotient space W/f(V) is the dimension of the target space minus the dimension of the image.

As a simple example, consider the map f: R² → R², given by f(x, y) = (0, y). Then for an equation f(x, y) = (a, b) to have a solution, we must have a = 0 (one constraint), and in that case the solution space is (x, b) or equivalently stated, (0, b) + (x, 0), (one degree of freedom). The kernel may be expressed as the subspace (x, 0) < V: the value of x is the freedom in a solution – while the cokernel may be expressed via the map W → R, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle (a, b) \mapsto (a)} : given a vector (a, b), the value of a is the obstruction to there being a solution.

An example illustrating the infinite-dimensional case is afforded by the map f: R^∞ → R^∞, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \left\{a_n\right\} \mapsto \left\{b_n\right\}} with b₁ = 0 and b_{n + 1} = a_n for n > 0. Its image consists of all sequences with first element 0, and thus its cokernel consists of the classes of sequences with identical first element. Thus, whereas its kernel has dimension 0 (it maps only the zero sequence to the zero sequence), its co-kernel has dimension 1. Since the domain and the target space are the same, the rank and the dimension of the kernel add up to the same sum as the rank and the dimension of the co-kernel (خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \aleph_0 + 0 = \aleph_0 + 1} ), but in the infinite-dimensional case it cannot be inferred that the kernel and the co-kernel of an endomorphism have the same dimension (0 ≠ 1). The reverse situation obtains for the map h: R^∞ → R^∞, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \left\{a_n\right\} \mapsto \left\{c_n\right\}} with c_n = a_{n + 1}. Its image is the entire target space, and hence its co-kernel has dimension 0, but since it maps all sequences in which only the first element is non-zero to the zero sequence, its kernel has dimension 1.

Index

For a linear operator with finite-dimensional kernel and co-kernel, one may define index as: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{ind}(f) := \dim(\ker(f)) - \dim(\operatorname{coker}(f)),} namely the degrees of freedom minus the number of constraints.

For a transformation between finite-dimensional vector spaces, this is just the difference dim(V) − dim(W), by rank–nullity. This gives an indication of how many solutions or how many constraints one has: if mapping from a larger space to a smaller one, the map may be onto, and thus will have degrees of freedom even without constraints. Conversely, if mapping from a smaller space to a larger one, the map cannot be onto, and thus one will have constraints even without degrees of freedom.

The index of an operator is precisely the Euler characteristic of the 2-term complex 0 → V → W → 0. In operator theory, the index of Fredholm operators is an object of study, with a major result being the Atiyah–Singer index theorem.^[15]

Algebraic classifications of linear transformations

No classification of linear maps could be exhaustive. The following incomplete list enumerates some important classifications that do not require any additional structure on the vector space.

Let $V$ and $W$ denote vector spaces over a field $F$ and let $T : V \to W$ be a linear map.

Monomorphism

T

is said to be injective or a monomorphism if any of the following equivalent conditions are true:

$T$ is one-to-one as a map of sets.
$ker T = {0 V}$
$dim(ker T) = 0$
$T$ is monic or left-cancellable, which is to say, for any vector space $U$ and any pair of linear maps $R : U \to V$ and $S : U \to V$ , the equation $TR = TS$ implies $R = S$ .
$T$ is left-invertible, which is to say there exists a linear map $S : W \to V$ such that $ST$ is the identity map on $V$ .

Epimorphism

T

is said to be surjective or an epimorphism if any of the following equivalent conditions are true:

$T$ is onto as a map of sets.
$coker T = {0 W}$
$T$ is epic or right-cancellable, which is to say, for any vector space $U$ and any pair of linear maps $R : W \to U$ and $S : W \to U$ , the equation $RT = ST$ implies $R = S$ .
$T$ is right-invertible, which is to say there exists a linear map $S : W \to V$ such that $TS$ is the identity map on $W$ .

Isomorphism

T

is said to be an isomorphism if it is both left- and right-invertible. This is equivalent to

T

being both one-to-one and onto (a bijection of sets) or also to

T

being both epic and monic, and so being a bimorphism.

If $T : V \to V$ is an endomorphism, then:

If, for some positive integer $n$ , the $n$ -th iterate of $T$ , $T n$ , is identically zero, then $T$ is said to be nilpotent.
If $T 2 = T$ , then $T$ is said to be idempotent
If $T = kI$ , where $k$ is some scalar, then $T$ is said to be a scaling transformation or scalar multiplication map; see scalar matrix.

Change of basis

Given a linear map which is an endomorphism whose matrix is A, in the basis B of the space it transforms vector coordinates [u] as [v] = A[u]. As vectors change with the inverse of B (vectors are contravariant) its inverse transformation is [v] = B[v'].

Substituting this in the first expression خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle B\left[v'\right] = AB\left[u'\right]} hence خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[v'\right] = B^{-1}AB\left[u'\right] = A'\left[u'\right].}

Therefore, the matrix in the new basis is A′ = B⁻¹AB, being B the matrix of the given basis.

Therefore, linear maps are said to be 1-co- 1-contra-variant objects, or type (1, 1) tensors.

Continuity

A linear transformation between topological vector spaces, for example normed spaces, may be continuous. If its domain and codomain are the same, it will then be a continuous linear operator. A linear operator on a normed linear space is continuous if and only if it is bounded, for example, when the domain is finite-dimensional.^[16] An infinite-dimensional domain may have discontinuous linear operators.

An example of an unbounded, hence discontinuous, linear transformation is differentiation on the space of smooth functions equipped with the supremum norm (a function with small values can have a derivative with large values, while the derivative of 0 is 0). For a specific example, $sin(nx)/ n$ converges to 0, but its derivative $cos(nx)$ does not, so differentiation is not continuous at 0 (and by a variation of this argument, it is not continuous anywhere).

Applications

A specific application of linear maps is for geometric transformations, such as those performed in computer graphics, where the translation, rotation and scaling of 2D or 3D objects is performed by the use of a transformation matrix. Linear mappings also are used as a mechanism for describing change: for example in calculus correspond to derivatives; or in relativity, used as a device to keep track of the local transformations of reference frames.

Another application of these transformations is in compiler optimizations of nested-loop code, and in parallelizing compiler techniques.

انظر أيضاً

هناك كتاب ، Linear Algebra/Linear Transformations، في معرفة الكتب.

Notes

^ "Linear transformations of $V$ into $V$ are often called linear operators on $V$ ." Rudin 1976
^ Let $V$ and $W$ be two real vector spaces. A mapping a from $V$ into $W$ Is called a 'linear mapping' or 'linear transformation' or 'linear operator' [...] from $V$ into $W$ , if
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle a(\mathbf u + \mathbf v) = a \mathbf u + a \mathbf v} for all خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf u,\mathbf v \in V} ,
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle a(\lambda \mathbf u) = \lambda a \mathbf u } for all خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf u \in V} and all real $λ$ . Bronshtein & Semendyayev 2004
^
Rudin 1991
Here are some properties of linear mappings خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda: X \to Y} whose proofs are so easy that we omit them; it is assumed that خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A \subset X} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle B \subset Y} :
1. خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda 0 = 0.}
2. If $A$ is a subspace (or a convex set, or a balanced set) the same is true of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda(A)}
3. If $B$ is a subspace (or a convex set, or a balanced set) the same is true of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda^{-1}(B)}
4. In particular, the set: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda^{-1}(\{0\}) = \{\mathbf x \in X: \Lambda \mathbf x = 0\} = {N}(\Lambda)} is a subspace of $X$ , called the null space of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} .
^ Rudin 1991. Suppose now that $X$ and $Y$ are vector spaces over the same scalar field. A mapping خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda: X \to Y} is said to be linear if خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda(\alpha \mathbf x + \beta \mathbf y) = \alpha \Lambda \mathbf x + \beta \Lambda \mathbf y} for all خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf x, \mathbf y \in X} and all scalars خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \beta} . Note that one often writes خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda \mathbf x} , rather than خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda(\mathbf x)} , when خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} is linear.
^ Rudin 1976. A mapping $A$ of a vector space $X$ into a vector space $Y$ is said to be a linear transformation if: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A\left(\mathbf{x}_1 + \mathbf{x}_2\right) = A\mathbf{x}_1 + A\mathbf{x}_2,\ A(c\mathbf{x}) = c A\mathbf{x}} for all خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf{x}, \mathbf{x}_1, \mathbf{x}_2 \in X} and all scalars $c$ . Note that one often writes خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A\mathbf{x}} instead of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A(\mathbf {x})} if $A$ is linear.
^ Rudin 1991. Linear mappings of $X$ onto its scalar field are called linear functionals.
^ "terminology - What does 'linear' mean in Linear Algebra?". Mathematics Stack Exchange. Retrieved 2021-02-17.
^ Wilansky 2013, pp. 21-26.
^ Rudin 1976 Suppose خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \left\{\mathbf{x}_1, \ldots, \mathbf{x}_n\right\}} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \left\{\mathbf{y}_1, \ldots, \mathbf{y}_m\right\}} are bases of vector spaces $X$ and $Y$ , respectively. Then every خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A \in L(X, Y)} determines a set of numbers خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle a_{i,j}} such that خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\mathbf{x}_j = \sum_{i=1}^m a_{i,j}\mathbf{y}_i\quad (1 \leq j \leq n).} It is convenient to represent these numbers in a rectangular array of $m$ rows and $n$ columns, called an $m$ by $n$ matrix: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A] = \begin{bmatrix} a_{1,1} & a_{1,2} & \ldots & a_{1,n} \\ a_{2,1} & a_{2,2} & \ldots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \ldots & a_{m,n} \end{bmatrix}} Observe that the coordinates خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle a_{i,j}} of the vector خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A\mathbf{x}_j} (with respect to the basis خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \{\mathbf{y}_1, \ldots, \mathbf{y}_m\}} ) appear in the j^th column of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle [A]} . The vectors خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A\mathbf{x}_j} are therefore sometimes called the column vectors of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle [A]} . With this terminology, the range of $A$ is spanned by the column vectors of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle [A]} .
^ Axler (2015) p. 52, § 3.3
^ Tu (2011), p. 19, § 3.1
^ Horn & Johnson 2013, 0.2.3 Vector spaces associated with a matrix or linear transformation, p. 6
^ ^أ ^ب Katznelson & Katznelson (2008) p. 52, § 2.5.1
^ ^أ ^ب Halmos (1974) p. 90, § 50
^ قالب:SpringerEOM: "The main question in index theory is to provide index formulas for classes of Fredholm operators ... Index theory has become a subject on its own only after M. F. Atiyah and I. Singer published their index theorems"
^
Rudin 1991 1.18 Theorem Let خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} be a linear functional on a topological vector space $X$ . Assume خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda \mathbf x \neq 0} for some خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf x \in X} . Then each of the following four properties implies the other three:
1. خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} is continuous
2. The null space خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle N(\Lambda)} is closed.
3. خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle N(\Lambda)} is not dense in $X$ .
4. خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} is bounded in some neighbourhood $V$ of 0.

ببليوجرافيا

Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.
Bronshtein, I. N.; Semendyayev, K. A. (2004). Handbook of Mathematics (4th ed.). New York: Springer-Verlag. ISBN 3-540-43491-7.
Halmos, Paul Richard (1974) [1958]. Finite-Dimensional Vector Spaces (2nd ed.). Springer. ISBN 0-387-90093-4.
Horn, Roger A.; Johnson, Charles R. (2013). Matrix Analysis (Second ed.). Cambridge University Press. ISBN 978-0-521-83940-2.
Katznelson, Yitzhak; Katznelson, Yonatan R. (2008). A (Terse) Introduction to Linear Algebra. American Mathematical Society. ISBN 978-0-8218-4419-9.
Lang, Serge (1987), Linear Algebra (Third ed.), New York: Springer-Verlag, ISBN 0-387-96412-6
قالب:Rudin Walter Functional Analysis
Rudin, Walter (1976). Principles of Mathematical Analysis. Walter Rudin Student Series in Advanced Mathematics (3rd ed.). New York: McGraw–Hill. ISBN 978-0-07-054235-8.
قالب:Rudin Walter Functional Analysis
قالب:Schaefer Wolff Topological Vector Spaces
قالب:Swartz An Introduction to Functional Analysis
Tu, Loring W. (2011). An Introduction to Manifolds (2nd ed.). Springer. ISBN 978-0-8218-4419-9.
قالب:Wilansky Modern Methods in Topological Vector Spaces

[1] "Linear transformations of $V$ into $V$ are often called linear operators on $V$ ." Rudin 1976

[2] Let $V$ and $W$ be two real vector spaces. A mapping a from $V$ into $W$ Is called a 'linear mapping' or 'linear transformation' or 'linear operator' [...] from $V$ into $W$ , if
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle a(\mathbf u + \mathbf v) = a \mathbf u + a \mathbf v} for all خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf u,\mathbf v \in V} ,
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle a(\lambda \mathbf u) = \lambda a \mathbf u } for all خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf u \in V} and all real $λ$ . Bronshtein & Semendyayev 2004

[3] Rudin 1991
Here are some properties of linear mappings خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda: X \to Y} whose proofs are so easy that we omit them; it is assumed that خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A \subset X} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle B \subset Y} :
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda 0 = 0.}
If $A$ is a subspace (or a convex set, or a balanced set) the same is true of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda(A)}
If $B$ is a subspace (or a convex set, or a balanced set) the same is true of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda^{-1}(B)}
In particular, the set: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda^{-1}(\{0\}) = \{\mathbf x \in X: \Lambda \mathbf x = 0\} = {N}(\Lambda)} is a subspace of $X$ , called the null space of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} .

[4] خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda 0 = 0.}

[5] If $A$ is a subspace (or a convex set, or a balanced set) the same is true of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda(A)}

[6] If $B$ is a subspace (or a convex set, or a balanced set) the same is true of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda^{-1}(B)}

[7] In particular, the set: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda^{-1}(\{0\}) = \{\mathbf x \in X: \Lambda \mathbf x = 0\} = {N}(\Lambda)} is a subspace of $X$ , called the null space of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} .

[4] Rudin 1991. Suppose now that $X$ and $Y$ are vector spaces over the same scalar field. A mapping خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda: X \to Y} is said to be linear if خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda(\alpha \mathbf x + \beta \mathbf y) = \alpha \Lambda \mathbf x + \beta \Lambda \mathbf y} for all خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf x, \mathbf y \in X} and all scalars خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \beta} . Note that one often writes خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda \mathbf x} , rather than خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda(\mathbf x)} , when خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} is linear.

[5] Rudin 1976. A mapping $A$ of a vector space $X$ into a vector space $Y$ is said to be a linear transformation if: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A\left(\mathbf{x}_1 + \mathbf{x}_2\right) = A\mathbf{x}_1 + A\mathbf{x}_2,\ A(c\mathbf{x}) = c A\mathbf{x}} for all خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf{x}, \mathbf{x}_1, \mathbf{x}_2 \in X} and all scalars $c$ . Note that one often writes خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A\mathbf{x}} instead of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A(\mathbf {x})} if $A$ is linear.

[6] Rudin 1991. Linear mappings of $X$ onto its scalar field are called linear functionals.

[7] "terminology - What does 'linear' mean in Linear Algebra?". Mathematics Stack Exchange. Retrieved 2021-02-17.

[FOOTNOTEWilansky201321-26-8] Wilansky 2013, pp. 21-26.

[9] Rudin 1976 Suppose خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \left\{\mathbf{x}_1, \ldots, \mathbf{x}_n\right\}} and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \left\{\mathbf{y}_1, \ldots, \mathbf{y}_m\right\}} are bases of vector spaces $X$ and $Y$ , respectively. Then every خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A \in L(X, Y)} determines a set of numbers خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle a_{i,j}} such that خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\mathbf{x}_j = \sum_{i=1}^m a_{i,j}\mathbf{y}_i\quad (1 \leq j \leq n).} It is convenient to represent these numbers in a rectangular array of $m$ rows and $n$ columns, called an $m$ by $n$ matrix: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A] = \begin{bmatrix} a_{1,1} & a_{1,2} & \ldots & a_{1,n} \\ a_{2,1} & a_{2,2} & \ldots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \ldots & a_{m,n} \end{bmatrix}} Observe that the coordinates خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle a_{i,j}} of the vector خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A\mathbf{x}_j} (with respect to the basis خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \{\mathbf{y}_1, \ldots, \mathbf{y}_m\}} ) appear in the j^th column of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle [A]} . The vectors خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle A\mathbf{x}_j} are therefore sometimes called the column vectors of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle [A]} . With this terminology, the range of $A$ is spanned by the column vectors of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle [A]} .

[10] Axler (2015) p. 52, § 3.3

[11] Tu (2011), p. 19, § 3.1

[12] Horn & Johnson 2013, 0.2.3 Vector spaces associated with a matrix or linear transformation, p. 6

[:0-13] أ ^ب Katznelson & Katznelson (2008) p. 52, § 2.5.1

[:1-14] أ ^ب Halmos (1974) p. 90, § 50

[15] قالب:SpringerEOM: "The main question in index theory is to provide index formulas for classes of Fredholm operators ... Index theory has become a subject on its own only after M. F. Atiyah and I. Singer published their index theorems"

[16] Rudin 1991 1.18 Theorem Let خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} be a linear functional on a topological vector space $X$ . Assume خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda \mathbf x \neq 0} for some خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbf x \in X} . Then each of the following four properties implies the other three:
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} is continuous
The null space خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle N(\Lambda)} is closed.
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle N(\Lambda)} is not dense in $X$ .
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} is bounded in some neighbourhood $V$ of 0.

[21] خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} is continuous

[22] The null space خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle N(\Lambda)} is closed.

[23] خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle N(\Lambda)} is not dense in $X$ .

[24] خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} is bounded in some neighbourhood $V$ of 0.

[25] خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda 0 = 0.}

[26] If $A$ is a subspace (or a convex set, or a balanced set) the same is true of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda(A)}

[27] If $B$ is a subspace (or a convex set, or a balanced set) the same is true of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda^{-1}(B)}

[28] In particular, the set: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda^{-1}(\{0\}) = \{\mathbf x \in X: \Lambda \mathbf x = 0\} = {N}(\Lambda)} is a subspace of $X$ , called the null space of خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} .

[29] خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} is continuous

[30] The null space خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle N(\Lambda)} is closed.

[31] خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle N(\Lambda)} is not dense in $X$ .

[32] خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\textstyle \Lambda} is bounded in some neighbourhood $V$ of 0.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

v t e الجبر الخطي
معادلة خطية	نظام المعادلات الخطية محدد(محدد مقتصر-صيغة كوشي-بينيه-قاعدة كرامر-حذف گاوس-جوردان) خوارزمية شتراسن
مصفوفات	نظرية المصفوفة جمع المصفوفات ضرب المصفوفات مصفوفة التحويلِ الأساسية متعددة حدود مميزة أثر مبرهنة كايلي-هاميلتون قيمة خاصة، شعاع خاص شكل جوردان الطبيعي رتبة مصفوفة معكوسة مصفوفة قابلة للعكس مقلوب كاذب مصفوفة مصاحبة تحويل الجداء نقطة مصفوفة متماثلة مصفوفة متعامدة مصفوفة متماثلة منحرفة نقل مترافق مصفوفة الوحدة مصفوفة هيرميتية ضد هيرميتي معرف إيجابي نصف معرف إيجابي مصفوفة إيجابية معرفة بفافي مصفوفة تقدير مصفوفة قطرية قطر رئيسي مصفوفة قطورة مصفوفة Tridiagonal مصفوفة هيسينبرگ مصفوفة مثلثية نظرية طيفية مصفوفة قياسية مصفوفة تويبليتز مصفوفة هانكل ر مصفوفة فانديرموند مصفوفة كتلوية مصفوفة متناثرة مصفوفة دفع هوية مصفوفة وودبوري مبرهنة بيرون-فروبانيوس
تفكيك مصفوفة	تفكيك تشوليسكي تفكيك لو تفكيك كيو آر نظرية طيفية تفكيك قيمة مفرد تفكيك شور تكملة شور
حسابات	تحويل هاوسهولدر طريقة مجموع المربعات الدنيا عملية گرام شميت
متجهات	ضرب قياسي مجموعة خطية امتداد خطي استقلال خطي أساس خطي شعاع تنسيقي
فضاء شعاعي	أمثلة الفراغات الشعاعية تحويل خطي تحويل گاليلي تحويل لورينتز فضاء عمود فضاء صف فضاء ملغي بطلان نظرية بطلان غريزة النموِ فضاء ثنائي دالة خطية تعامد (جبر خطي) متمم متعامد إسقاط متعامد دوران غير صحيح فضاء جزئي
جبر متعدد الخطية	تينسور (معالجة كلاسيكية للتينسورات - معالجة متوسطة للتينسور - معالجة خالية من التنسورات) - موتر جبر خارجي جبر متماثل
فضاء تآلفي	تحويل أفيني زمرة أفينية هندسة تآلفية
فضاء إسقاطي	تحويل إسقاطي هندسة إسقاطية سطح الدرجة الثانية
تصنيف موضوعات بوابة كتب