توزيع احتمالي طبيعي

"المنحنى الجرسي" تحوّل إلى هنا. لمطالعة استخدامات أخرى، انظر المنحنى الجرسي (توضيح).

Normal distribution

Probability density function 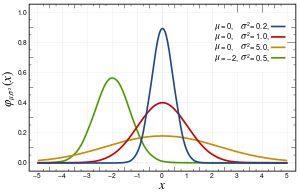The red curve is the standard normal distribution
Cumulative distribution function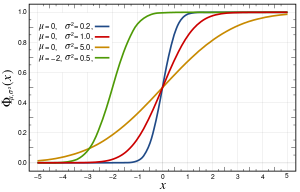
الترميز	${\mathcal {N}}(\mu ,\sigma ^{2})$
الوسائط	$\mu \in \mathbb {R}$ = mean (location) $\sigma ^{2}\in \mathbb {R} _{>0}$ = variance (squared scale)
الحامل	$x\in \mathbb {R}$
PDF	${\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$
CDF	${\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]$
القسيمة	$\mu +\sigma {\sqrt {2}}\operatorname {erf} ^{-1}(2p-1)$
المتوسط	$\mu$
أوسط	$\mu$
منوال	$\mu$
تباين	$\sigma ^{2}$
MAD	$\sigma {\sqrt {2/\pi }}$
تخالف	$0$
تدبب زائد	$0$
الاعتلاج	${\frac {1}{2}}\ln(2\pi \sigma ^{2})+{\frac {1}{2}}$
MGF	$\exp(\mu t+\sigma ^{2}t^{2}/2)$
CF	$\exp(i\mu t-\sigma ^{2}t^{2}/2)$
معلومات فيشر	${\mathcal {I}}(\mu ,\sigma )={\begin{pmatrix}1/\sigma ^{2}&0\\0&2/\sigma ^{2}\end{pmatrix}}$ ${\mathcal {I}}(\mu ,\sigma ^{2})={\begin{pmatrix}1/\sigma ^{2}&0\\0&1/(2\sigma ^{4})\end{pmatrix}}$
تباعد كولباخ-لايبلر	${1 \over 2}\left\{\left({\frac {\sigma _{0}}{\sigma _{1}}}\right)^{2}+{\frac {(\mu _{1}-\mu _{0})^{2}}{\sigma _{1}^{2}}}-1+\ln {\sigma _{1}^{2} \over \sigma _{0}^{2}}\right\}$

في نظرية الاحتمالات، التوزيع الطبيعي (أو الغاوسي) هو توزيع احتمالي مستمر يستخدم غالباً كتقريب أولي لوصف المتغيرات العشوائية التي تميل إلى التمركز حول قيمة متوسطة وحيدة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 نبذة من الأسس

إن لمخطط تابع كثافة الاحتمال المقابل لهذا التوزيع شكل الـناقوس ، ويعرف بالتابع الغاوسي أو منحني الجرس.

$f(x)={\tfrac {1}{\sqrt {2\pi \sigma ^{2}}}}\;e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}},$

حيث μ هو القيمة المتوقعة (مكان الذروة)، وσ² هو التباين (قياس عرض التوزيع). عندما تكون قيم وسيطي التوزيع μ = 0 وσ² = 1 فإنه يسمى التوزيع الطبيعي المعياري.

يعد التوزيع الطبيعي التوزيع الاحتمالي المستمر الأساسي، نظراً لدوره في مبرهنة النهاية المركزية، كما أنه من أول التوزيعات المستمرة التي تدرس في مقررات الإحصاء الابتدائية. فوفقاً لمبرهنة النهاية المركزية، وتحت شروط معينة، فإن مجموع عدد من المتغيرات العشوائية بعدد منته من المتوسطات والتباينات يقارب توزيعاً طبيعياً بازدياد عدد تلك المتغيرات. ولهذا السبب، فإنه كثيراً ما يشاهد هذا التوزيع في الممارسة العملية، وهو يستخدم في الإحصاء، والعلوم الطبيعية، والعلوم الاجتماعية كنموذج بسيط للتعامل مع ظواهر معقدة. وعلى سبيل المثال، فإن خطأ الملاحظة في تجربة ما، غالباً ما يتبع توزيعاً طبيعياً. كما يحسب انتشار اللايقين propagation of uncertainty باستخدام هذا الافتراض أيضاً.

لاحظ أن لمتغير ذي توزع طبيعي توزيعاً متناظراً حول متوسطه. ولهذا فإن القيم التي تنمو بشكل أسي (كالأسعار، والدخول، وعدد السكان) تكون ملتوية نحو يمين (skewness)، وبالتالي يمكن التعبير عنها بشكل أفضل باستخدام توزيعات أخرى، كالتوزيع الطبيعي اللوغاريتمي log-normal distribution، وتوزيع بارتو Pareto distribution.

 التوزيع الطبيعي الموسّط المختزل

الدالّة $\varphi :\mathbb {R} \to \mathbb {R} ^{+}$ بحيث $\varphi (t)={\frac {1}{\sqrt {2\;\pi }}}\,\mathrm {e} ^{-{\frac {t^{2}}{2}}}$

هي دالة دالة كثافة احتمالية : هي متواصلة وتكاملها على $\ \mathbb {R}$ يساوي 1.

فاننا نعلم أن $\ \int _{-\infty }^{+\infty }\mathrm {e} ^{-{\frac {t^{2}}{2}}}\ dt={\sqrt {2\,\pi }}$ (تكامل غاوس).

ونبين أن (أنظر التالي) التوزيع الذي يقع تحديده انطلاقا من دالة الكثافة هذه له قيمة متوقعة تساوى 0 وتباينا يساوي 0.

ملاحظات

• الكثافة $\varphi$ نظيرة
• يمكن اشتقاق هذه الدالة عددا لا متناهيا من المرّات وتحقق مهما كان $\ t\in \mathbb {R}$ المعادلة التالية $\varphi '(t)=-t\,\varphi (t)$.

 التعريف

نسمي التوزيع الطبيعي (أو غاوسي) موسّط مختزل التوزيع المعرّف بدالة الكثافة $\varphi$.

الرسم البياني لهذه الكثافة يمثل شكل جرس.

 التوزيع التراكمي

لتكن $\Phi$ دالة التوزيع التراكمي (Cumulative distribution function-Fonction de répartition) للتوزيع الموسّط المختزل. تحدد لكل عدد حقيقي x ب:

$\ \Phi (x)=\int _{-\infty }^{x}\varphi (t)\,dt=\int _{-\infty }^{x}{\frac {1}{\sqrt {2\,\pi }}}\,\mathrm {e} ^{-{\frac {t^{2}}{2}}}\,dt$.

وهي تكامل $\varphi$ ونهايتها في $-\infty$ تساوي 0، ولا يمكن كتابتها باستعمال الدالات المعروفة (أس، جيب..) ولكن تصبح هي بنفسها دالة مستعملة بكثرة ومهمّة لكلّ من يمارس حساب الاحتمالات والإحصاء.

خاصيات الدالة $\Phi$ :

• قابلة للاشتقاق بعدد غير متناهي من المرّات و $\Phi '=\varphi$.
• نامية حصريا وتنتهي إلى 0 في $-\infty$ و إلى 1 في $+\infty$.

Therefore here are some trivial results from area under bell curve -

$\Phi ({-\infty })=0=0\%$

$\Phi (0)=0.5=50\%$

$\Phi ({\infty })=1=100\%$

$\Phi (x)=1-\Phi (-x)$ and therefore $\Phi (x)+\Phi (-x)=100\%$

In statistics one often uses the related error function, or erf(x), defined as the probability of a random variable with normal distribution of mean 0 and variance 1/2 falling in the range $[-x,x]$; that is

$\operatorname {erf} (x)\;=\;{\frac {1}{\sqrt {\pi }}}\int _{-x}^{x}e^{-t^{2}}\,dt$

These integrals cannot be expressed in terms of elementary functions, and are often said to be special functions *. They are closely related, namely

$\Phi (x)\;=\;{\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]$

For a generic normal distribution f with mean μ and deviation σ, the cumulative distribution function is

$F(x)\;=\;\Phi \left({\frac {x-\mu }{\sigma }}\right)\;=\;{\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]$

The complement of the standard normal CDF, $Q(x)=1-\Phi (x)$, is often called the Q-function, especially in engineering texts. It gives the probability that the value of a standard normal random variable X will exceed x. Other definitions of the Q-function, all of which are simple transformations of $\Phi$, are also used occasionally.

• The cumulative distribution function (CDF) of the standard normal distribution can be expand by Integration by parts into a series:

$\Phi (x)\;=\;0.5+{\frac {1}{\sqrt {2\pi }}}\cdot e^{-x^{2}/2}\left[x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+...+{\frac {x^{2n+1}}{3\cdot 5\cdot 7\cdot ...\cdot (2n+1)}}\right]$

Example of Pascal function to calculate CDF (sum of first 100 elements)

function CDF(x:extended):extended;
var value,sum:extended;
    i:integer;
begin
  sum:=x;
  value:=x;
  for i:=1 to 100 do
    begin
      value:=(value*x*x/(2*i+1));
      sum:=sum+value;
    end;
  result:=0.5+(sum/sqrt(2*pi))*exp(-(x*x)/2);
end;

 Standard deviation and tolerance intervals

المقالة الرئيسية: Tolerance interval

Dark blue is less than one standard deviation away from the mean. For the normal distribution, this accounts for about 68% of the set, while two standard deviations from the mean (medium and dark blue) account for about 95%, and three standard deviations (light, medium, and dark blue) account for about 99.7%.

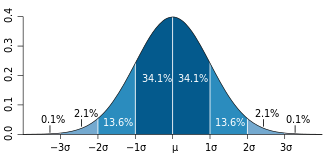
About 68% of values drawn from a normal distribution are within one standard deviation σ away from the mean; about 95% of the values lie within two standard deviations; and about 99.7% are within three standard deviations. This fact is known as the 68-95-99.7 (empirical) rule, or the 3-sigma rule.

More precisely, the probability that a normal deviate lies in the range μ − nσ and μ + nσ is given by

$F(\mu +n\sigma )-F(\mu -n\sigma )=\Phi (n)-\Phi (-n)=\mathrm {erf} \left({\frac {n}{\sqrt {2}}}\right),$

To 12 decimal places, the values for n = 1, 2, ..., 6 are:

n	F(μ+nσ) − F(μ−nσ)	i.e. 1 minus ...	or 1 in ...	OEIS
1	0.682689492137	0.317310507863	3.15148718753	OEIS: A178647
2	0.954499736104	0.045500263896	21.9778945080	OEIS: A110894
3	0.997300203937	0.002699796063	370.398347345
4	0.999936657516	0.000063342484	15787.1927673
5	0.999999426697	0.000000573303	1744277.89362
6	0.999999998027	0.000000001973	506797345.897

 Quantile function

The quantile function of a distribution is the inverse of the cumulative distribution function. The quantile function of the standard normal distribution is called the probit function, and can be expressed in terms of the inverse error function:

$\Phi ^{-1}(p)\;=\;{\sqrt {2}}\;\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$

For a normal random variable with mean μ and variance σ², the quantile function is

$F^{-1}(p)=\mu +\sigma \Phi ^{-1}(p)=\mu +\sigma {\sqrt {2}}\,\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$

The quantile $\Phi ^{-1}(p)$ of the standard normal distribution is commonly denoted as z_p. These values are used in hypothesis testing, construction of confidence intervals and Q-Q plots. A normal random variable X will exceed μ + σz_p with probability 1−p; and will lie outside the interval μ ± σz_p with probability 2(1−p). In particular, the quantile z_0.975 is 1.96; therefore a normal random variable will lie outside the interval μ ± 1.96σ in only 5% of cases.

The following table gives the multiple n of σ such that X will lie in the range μ ± nσ with a specified probability p. These values are useful to determine tolerance interval for sample averages and other statistical estimators with normal (or asymptotically normal) distributions:

F(μ+nσ) − F(μ−nσ)	n		F(μ+nσ) − F(μ−nσ)	n
0.80	1.281551565545		0.999	3.290526731492
0.90	1.644853626951		0.9999	3.890591886413
0.95	1.959963984540		0.99999	4.417173413469
0.98	2.326347874041		0.999999	4.891638475699
0.99	2.575829303549		0.9999999	5.326723886384
0.995	2.807033768344		0.99999999	5.730728868236
0.998	3.090232306168		0.999999999	6.109410204869

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 The central limit theorem

As the number of discrete events increases, the function begins to resemble a normal distribution

Comparison of probability density functions, p(k) for the sum of n fair 6-sided dice to show their convergence to a normal distribution with increasing n, in accordance to the central limit theorem. In the bottom-right graph, smoothed profiles of the previous graphs are rescaled, superimposed and compared with a normal distribution (black curve).

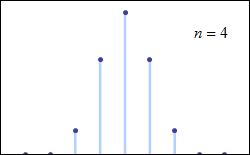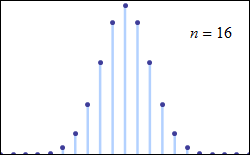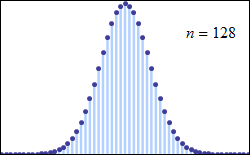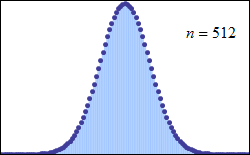
المقالة الرئيسية: Central limit theorem

 انظر أيضاً

• مشكلة برنز-فيشر — the long-standing problem of testing whether two normal samples with different variances have same means;
• Bhattacharyya distance– method used to separate mixtures of normal distributions
• مبرهنة إردوس-كاتش — on the occurrence of the normal distribution في نظرية الأعداد
• Gaussian blur — convolution which uses the normal distribution as a kernel
• Sum of normally distributed random variables
• Normally distributed and uncorrelated does not imply independent
• Tweedie distributions — The normal distribution is a member of the family of Tweedie exponential dispersion models
• Z-test— using the normal distribution
• Rayleigh distribution

 وصلات خارجية

• Hazewinkel, Michiel, ed. (2001), "Normal distribution", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• Normal Distribution Video Tutorial Part 1-2
• An 8-foot-tall (2.4 m) Probability Machine (named Sir Francis) comparing stock market returns to the randomness of the beans dropping through the quincunx pattern. YouTube link originating from Index Funds Advisors