براهماجوبتا
براهماگوپتا Brahmagupta | |
|---|---|
 | |
| وُلِدَ | 598 م |
| توفي | ح. 668 CE (aged c. 69–70) |
| عـُرِف بـ | |
| السيرة العلمية | |
| المجالات | الرياضيات، الفلك |
براهماجوبتا أو براهماگوپتا (بالسنسكريتية: ब्रह्मगुप्त; استمع ؛ إنگليزية: Brahmagupta) (597–668 م) كان عالم رياضيات وفلك هندي كتب عملين هامين في الرياضيات والفلك: براهماسفوطاسيدانتا (عمل براهما الضخم) (628)، العمل النظري، وKhaṇḍakhādyaka، وهو نص أكثر عملية. وهناك أسباب للاعتقاد أن براهماگوپتا ينحدر من بهينمال.
براهماگوپتا كان أول من أعطى قواعد للحساب باستخدم الصفر. النصوص التي ألفها براهماگوپتا كانت مكتوبة بسجع ملتوي، كما كان التقليد في الرياضيات الهندية، ولذلك فلها جرْس شاعري. He is the author of two early works on mathematics and astronomy: the Brāhmasphuṭasiddhānta (BSS, "correctly established doctrine of Brahma", dated 628), a theoretical treatise, and the Khaṇḍakhādyaka ("edible bite", dated 665), a more practical text.
In 628 CE, Brahmagupta first described gravity as an attractive force, and used the term "gurutvākarṣaṇam (गुरुत्वाकर्षणम्)" in Sanskrit to describe it.[1][2][3][4]
Brahmagupta is credited with first clear description of the quadratic formula (the solution of the quadratic equation)[5] in his main work, the Brāhma-sphuṭa-siddhānta.[6]
الحياة والعمل
Brahmagupta, according to his own statement, was born in 598 CE. Born in Bhillamāla in Gurjaradesa[7] (modern Bhinmal in Rajasthan, India) during the reign of the Chavda dynasty ruler Vyagrahamukha, his ancestors were probably from Sindh.[8][9] He was the son of Jishnugupta and was a Hindu by religion, in particular, a Shaivite.[10] He lived and worked there for a good part of his life. Prithudaka Svamin, a later commentator, called him Bhillamalacharya, the teacher from Bhillamala.[11]
Bhillamala was the capital of the Gurjaradesa, the second-largest kingdom of Western India, comprising southern Rajasthan and northern Gujarat in modern-day India. It was also a centre of learning for mathematics and astronomy. He became an astronomer of the Brahmapaksha school, one of the four major schools of Indian astronomy during this period. He studied the five traditional Siddhantas on Indian astronomy as well as the work of other astronomers including Aryabhata I, Latadeva, Pradyumna, Varahamihira, Simha, Srisena, Vijayanandin and Vishnuchandra. [11]
In the year 628, at the age of 30, he composed the Brāhmasphuṭasiddhānta ("improved treatise of Brahma") which is believed to be a revised version of the received Siddhanta of the Brahmapaksha school of astronomy. Scholars state that he incorporated a great deal of originality into his revision, adding a considerable amount of new material. The book consists of 24 chapters with 1008 verses in the ārya metre. A good deal of it is astronomy, but it also contains key chapters on mathematics, including algebra, geometry, trigonometry and algorithmics, which are believed to contain new insights due to Brahmagupta himself.[11][12][13]
Later, Brahmagupta moved to Ujjaini, Avanti,[14] a major centre for astronomy in central India. At the age of 67, he composed his next well-known work Khanda-khādyaka, a practical manual of Indian astronomy in the karana category meant to be used by students.[14]
Brahmagupta died in 668 CE, and he is presumed to have died in Ujjain.
مؤلفاته
ألف سنة 628م كتابا فلكيا رياضيا أساسيا أسمه براهمسپهطسدهانت (كتاب) سارت على نهجه الدراسات الفلكية الأولى في العالم الإسلامي. حيث ترجم مختصر له الى اللغة العربية بأمر من الخليفة المنصور العباسي.
- كتابا آخر في الحسابات الفلكية أسمه (خاندا خاياكا) فسر فيه مجموعة آريابهاتا الفلكية.
- Grahaṇārkajñāna,[15] (ascribed in one manuscript)
حارب براهماگويتا أفكارا فلكية صحيحة كدوران الأرض حول محورها التى قال بها آريابهاتا.
Reception
Brahmagupta's mathematical advances were carried on further by Bhāskara II, a lineal descendant in Ujjain, who described Brahmagupta as the ganaka-chakra-chudamani (the gem of the circle of mathematicians). Prithudaka Svamin wrote commentaries on both of his works, rendering difficult verses into simpler language and adding illustrations. Lalla and Bhattotpala in the 8th and 9th centuries wrote commentaries on the Khanda-khadyaka.[16] Further commentaries continued to be written into the 12th century.[14]
A few decades after the death of Brahmagupta, Sindh came under the Arab Caliphate in 712 CE. Expeditions were sent into Gurjaradesa ("Al-Baylaman in Jurz", as per Arab historians). The kingdom of Bhillamala seems to have been annihilated but Ujjain repulsed the attacks. The court of Caliph Al-Mansur (754–775) received an embassy from Sindh, including an astrologer called Kanaka, who brought (possibly memorised) astronomical texts, including those of Brahmagupta. Brahmagupta's texts were translated into Arabic by Muhammad al-Fazari, an astronomer in Al-Mansur's court, under the names Sindhind and Arakhand. An immediate outcome was the spread of the decimal number system used in the texts. The mathematician Al-Khwarizmi (800–850 CE) wrote a text called al-Jam wal-tafriq bi hisal-al-Hind (Addition and Subtraction in Indian Arithmetic), which was translated into Latin in the 13th century as Algorithmi de numero indorum. Through these texts, the decimal number system and Brahmagupta's algorithms for arithmetic have spread throughout the world. Al-Khwarizmi also wrote his own version of Sindhind, drawing on Al-Fazari's version and incorporating Ptolemaic elements. Indian astronomic material circulated widely for centuries, even making its way into medieval Latin texts.[17][18][19]
The historian of science George Sarton called Brahmagupta "one of the greatest scientists of his race and the greatest of his time."[14]
الرياضيات
الجبر
Brahmagupta gave the solution of the general linear equation in chapter eighteen of Brahmasphuṭasiddhānta,
The difference between rupas, when inverted and divided by the difference of the [coefficients] of the [unknowns], is the unknown in the equation. The rupas are [subtracted on the side] below that from which the square and the unknown are to be subtracted.[20]
which is a solution for the equation bx + c = dx + e where rupas refers to the constants c and e. The solution given is equivalent to x = e − c/b − d.
He further gave two equivalent solutions to the general quadratic equation
18.44. Diminish by the middle [number] the square-root of the rupas multiplied by four times the square and increased by the square of the middle [number]; divide the remainder by twice the square. [The result is] the middle [number].
18.45. Whatever is the square-root of the rupas multiplied by the square [and] increased by the square of half the unknown, diminished that by half the unknown [and] divide [the remainder] by its square. [The result is] the unknown.[20]
which are, respectively, solutions for the equation ax2 + bx = c equivalent to,
and
He went on to solve systems of simultaneous indeterminate equations stating that the desired variable must first be isolated, and then the equation must be divided by the desired variable's coefficient. In particular, he recommended using "the pulverizer" to solve equations with multiple unknowns.
18.51. Subtract the colors different from the first color. [The remainder] divided by the first [color's coefficient] is the measure of the first. [Terms] two by two [are] considered [when reduced to] similar divisors, [and so on] repeatedly. If there are many [colors], the pulverizer [is to be used].[20]
Like the algebra of Diophantus, the algebra of Brahmagupta was syncopated. Addition was indicated by placing the numbers side by side, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, similar to our notation but without the bar. Multiplication, evolution, and unknown quantities were represented by abbreviations of appropriate terms.[21] The extent of Greek influence on this syncopation, if any, is not known and it is possible that both Greek and Indian syncopation may be derived from a common Babylonian source.[21]
الحساب
The four fundamental operations (addition, subtraction, multiplication, and division) were known to many cultures before Brahmagupta. This current system is based on the Hindu–Arabic numeral system and first appeared in the Brāhmasphuṭasiddhānta. Brahmagupta describes multiplication in the following way:
The multiplicand is repeated like a string for cattle, as often as there are integrant portions in the multiplier and is repeatedly multiplied by them and the products are added together. It is multiplication. Or the multiplicand is repeated as many times as there are component parts in the multiplier.[22]
Indian arithmetic was known in Medieval Europe as modus Indorum meaning "method of the Indians". In the Brāhmasphuṭasiddhānta, four methods for multiplication were described, including gomūtrikā, which is said to be close to the present day methods.[23] In the beginning of chapter twelve of his Brāhmasphuṭasiddhānta, entitled "Calculation", he also details operations on fractions. The reader is expected to know the basic arithmetic operations as far as taking the square root, although he explains how to find the cube and cube-root of an integer and later gives rules facilitating the computation of squares and square roots. He then gives rules for dealing with five types of combinations of fractions: a/c + b/c; a/c × b/d; a/1 + b/d; a/c + b/d × a/c = a(d + b)/cd; and a/c − b/d × a/c = a(d − b)/cd.[24]
Squares and Cubes
Brahmagupta then goes on to give the sum of the squares and cubes of the first n integers.
12.20. The sum of the squares is that [sum] multiplied by twice the [number of] step[s] increased by one [and] divided by three. The sum of the cubes is the square of that [sum] Piles of these with identical balls [can also be computed].[25]
Here Brahmagupta found the result in terms of the sum of the first n integers, rather than in terms of n as is the modern practice.[26]
He gives the sum of the squares of the first n natural numbers as n(n + 1)(2n + 1)/6 and the sum of the cubes of the first n natural numbers as (n(n + 1)/2)2 .
Zero
Brahmagupta's Brahmasphuṭasiddhānta is the first book that provides rules for arithmetic manipulations that apply to zero and to negative numbers.[27] The Brāhmasphuṭasiddhānta is the earliest known text to treat zero as a number in its own right, rather than as simply a placeholder digit in representing another number as was done by the Babylonians or as a symbol for lack of quantity as was done by Ptolemy and the Romans. In chapter eighteen of his Brāhmasphuṭasiddhānta, Brahmagupta describes operations on negative numbers. He first describes addition and subtraction,
18.30. [The sum] of two positives is positives, of two negatives negative; of a positive and a negative [the sum] is their difference; if they are equal it is zero. The sum of a negative and zero is negative, [that] of a positive and zero positives, [and that] of two zeros zero.
[...]
18.32. A negative minus zero is negative, a positive [minus zero] is positive; zero [minus zero] is zero. When a positive is to be subtracted from a negative or a negative from a positive, then it is to be added.[20]
He goes on to describe multiplication,
18.33. The product of a negative and a positive is negative, of two negatives positive, and of positives positive; the product of zero and a negative, of zero and a positive, or of two zeros is zero.[20]
But his description of division by zero differs from our modern understanding:
18.34. A positive divided by a positive or a negative divided by a negative is positive; a zero divided by zero is zero; a positive divided by a negative is negative; a negative divided by a positive is [also] negative.
18.35. A negative or a positive divided by zero has that [zero] as its divisor, or zero divided by a negative or a positive [has that negative or positive as its divisor]. The square of a negative or positive is positive; [the square] of zero is zero. That of which [the square] is the square is [its] square root.[20]
Here Brahmagupta states that 0/0 = 0 and as for the question of a/0 where a ≠ 0 he did not commit himself.[28] His rules for arithmetic on negative numbers and zero are quite close to the modern understanding, except that in modern mathematics division by zero is left undefined.
التحليل الديوفانتي
الثلاثيات الفيثاغورية
In chapter twelve of his Brāhmasphuṭasiddhānta, Brahmagupta provides a formula useful for generating Pythagorean triples:
12.39. The height of a mountain multiplied by a given multiplier is the distance to a city; it is not erased. When it is divided by the multiplier increased by two it is the leap of one of the two who make the same journey.[29]
Or, in other words, if d = mx/x + 2, then a traveller who "leaps" vertically upwards a distance d from the top of a mountain of height m, and then travels in a straight line to a city at a horizontal distance mx from the base of the mountain, travels the same distance as one who descends vertically down the mountain and then travels along the horizontal to the city.[29] Stated geometrically, this says that if a right-angled triangle has a base of length a = mx and altitude of length b = m + d, then the length, c, of its hypotenuse is given by c = m(1 + x) − d. And, indeed, elementary algebraic manipulation shows that a2 + b2 = c2 whenever d has the value stated. Also, if m and x are rational, so are d, a, b and c. A Pythagorean triple can therefore be obtained from a, b and c by multiplying each of them by the least common multiple of their denominators.
معادلة پل
Brahmagupta went on to give a recurrence relation for generating solutions to certain instances of Diophantine equations of the second degree such as Nx2 + 1 = y2 (called Pell's equation) by using the Euclidean algorithm. The Euclidean algorithm was known to him as the "pulverizer" since it breaks numbers down into ever smaller pieces.[30]
The nature of squares:
18.64. [Put down] twice the square-root of a given square by a multiplier and increased or diminished by an arbitrary [number]. The product of the first [pair], multiplied by the multiplier, with the product of the last [pair], is the last computed.
18.65. The sum of the thunderbolt products is the first. The additive is equal to the product of the additives. The two square-roots, divided by the additive or the subtractive, are the additive rupas.[20]
The key to his solution was the identity,[31]
which is a generalisation of an identity that was discovered by Diophantus,
Using his identity and the fact that if (x1, y1) and (x2, y2) are solutions to the equations x2 − Ny2 = k1 and x2 − Ny2 = k2, respectively, then (x1x2 + Ny1y2, x1y2 + x2y1) is a solution to x2 − Ny2 = k1k2, he was able to find integral solutions to Pell's equation through a series of equations of the form x2 − Ny2 = ki. Brahmagupta was not able to apply his solution uniformly for all possible values of N, rather he was only able to show that if x2 − Ny2 = k has an integer solution for k = ±1, ±2, or ±4, then x2 − Ny2 = 1 has a solution. The solution of the general Pell's equation would have to wait for Bhāskara II in ح. 1150 CE.[31]
الهندسة
صيغة پراهماگوپتا
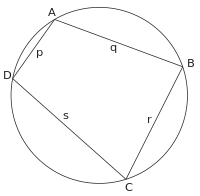
Brahmagupta's most famous result in geometry is his formula for cyclic quadrilaterals. Given the lengths of the sides of any cyclic quadrilateral, Brahmagupta gave an approximate and an exact formula for the figure's area,
12.21. The approximate area is the product of the halves of the sums of the sides and opposite sides of a triangle and a quadrilateral. The accurate [area] is the square root from the product of the halves of the sums of the sides diminished by [each] side of the quadrilateral.[25]
So given the lengths p, q, r and s of a cyclic quadrilateral, the approximate area is p + r/2 · q + s/2 while, letting t = p + q + r + s/2, the exact area is
- √(t − p)(t − q)(t − r)(t − s).
Although Brahmagupta does not explicitly state that these quadrilaterals are cyclic, it is apparent from his rules that this is the case.[32] Heron's formula is a special case of this formula and it can be derived by setting one of the sides equal to zero.
المثلثات
Brahmagupta dedicated a substantial portion of his work to geometry. One theorem gives the lengths of the two segments a triangle's base is divided into by its altitude:
12.22. The base decreased and increased by the difference between the squares of the sides divided by the base; when divided by two they are the true segments. The perpendicular [altitude] is the square-root from the square of a side diminished by the square of its segment.[25]
Thus the lengths of the two segments are 1/2(b ± c2 − a2/b).
He further gives a theorem on rational triangles. A triangle with rational sides a, b, c and rational area is of the form:
for some rational numbers u, v, and w.[33]
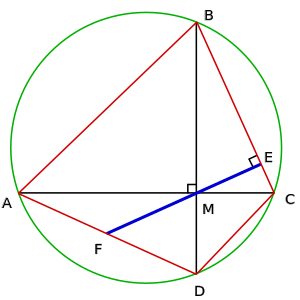
مبرهنة پراهماگوپتا
 مقالة مفصلة: مبرهنة پراهماگوپتا
مقالة مفصلة: مبرهنة پراهماگوپتا
Brahmagupta continues,
12.23. The square-root of the sum of the two products of the sides and opposite sides of a non-unequal quadrilateral is the diagonal. The square of the diagonal is diminished by the square of half the sum of the base and the top; the square-root is the perpendicular [altitudes].[25]
So, in a "non-unequal" cyclic quadrilateral (that is, an isosceles trapezoid), the length of each diagonal is √pr + qs.
He continues to give formulas for the lengths and areas of geometric figures, such as the circumradius of an isosceles trapezoid and a scalene quadrilateral, and the lengths of diagonals in a scalene cyclic quadrilateral. This leads up to Brahmagupta's famous theorem,
12.30–31. Imaging two triangles within [a cyclic quadrilateral] with unequal sides, the two diagonals are the two bases. Their two segments are separately the upper and lower segments [formed] at the intersection of the diagonals. The two [lower segments] of the two diagonals are two sides in a triangle; the base [of the quadrilateral is the base of the triangle]. Its perpendicular is the lower portion of the [central] perpendicular; the upper portion of the [central] perpendicular is half of the sum of the [sides] perpendiculars diminished by the lower [portion of the central perpendicular].[25]
ط
In verse 40, he gives values of π,
12.40. The diameter and the square of the radius [each] multiplied by 3 are [respectively] the practical circumference and the area [of a circle]. The accurate [values] are the square-roots from the squares of those two multiplied by ten.[25]
So Brahmagupta uses 3 as a "practical" value of π, and as an "accurate" value of π, with an error less than 1%.
Measurements and constructions
In some of the verses before verse 40, Brahmagupta gives constructions of various figures with arbitrary sides. He essentially manipulated right triangles to produce isosceles triangles, scalene triangles, rectangles, isosceles trapezoids, isosceles trapezoids with three equal sides, and a scalene cyclic quadrilateral.
After giving the value of pi, he deals with the geometry of plane figures and solids, such as finding volumes and surface areas (or empty spaces dug out of solids). He finds the volume of rectangular prisms, pyramids, and the frustum of a square pyramid. He further finds the average depth of a series of pits. For the volume of a frustum of a pyramid, he gives the "pragmatic" value as the depth times the square of the mean of the edges of the top and bottom faces, and he gives the "superficial" volume as the depth times their mean area.[34]
Trigonometry
Sine table
In Chapter 2 of his Brāhmasphuṭasiddhānta, entitled Planetary True Longitudes, Brahmagupta presents a sine table:
2.2–5. The sines: The Progenitors, twins; Ursa Major, twins, the Vedas; the gods, fires, six; flavors, dice, the gods; the moon, five, the sky, the moon; the moon, arrows, suns [...][35]
Here Brahmagupta uses names of objects to represent the digits of place-value numerals, as was common with numerical data in Sanskrit treatises. Progenitors represents the 14 Progenitors ("Manu") in Indian cosmology or 14, "twins" means 2, "Ursa Major" represents the seven stars of Ursa Major or 7, "Vedas" refers to the 4 Vedas or 4, dice represents the number of sides of the traditional die or 6, and so on. This information can be translated into the list of sines, 214, 427, 638, 846, 1051, 1251, 1446, 1635, 1817, 1991, 2156, 2312, 2459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, and 3270, with the radius being 3270 (this numbers represent for ).[36]
Interpolation formula
In 665 Brahmagupta devised and used a special case of the Newton–Stirling interpolation formula of the second-order to interpolate new values of the sine function from other values already tabulated.[37] The formula gives an estimate for the value of a function f at a value a + xh of its argument (with h > 0 and −1 ≤ x ≤ 1) when its value is already known at a − h, a and a + h.
The formula for the estimate is:
where Δ is the first-order forward-difference operator, i.e.
Early concept of gravity
Brahmagupta in 628 first described gravity as an attractive force, using the term "gurutvākarṣaṇam (गुरुत्वाकर्षणम्)" to describe it:[1][2][3][4]
The earth on all its sides is the same; all people on the earth stand upright, and all heavy things fall down to the earth by a law of nature, for it is the nature of the earth to attract and to keep things, as it is the nature of water to flow ... If a thing wants to go deeper down than the earth, let it try. The earth is the only low thing, and seeds always return to it, in whatever direction you may throw them away, and never rise upwards from the earth.[38][39][أ]
علم الفلك
Brahmagupta directed a great deal of criticism towards the work of rival astronomers, and his Brāhmasphuṭasiddhānta displays one of the earliest schisms among Indian mathematicians. The division was primarily about the application of mathematics to the physical world, rather than about the mathematics itself. In Brahmagupta's case, the disagreements stemmed largely from the choice of astronomical parameters and theories.[40] Critiques of rival theories appear throughout the first ten astronomical chapters and the eleventh chapter is entirely devoted to criticism of these theories, although no criticisms appear in the twelfth and eighteenth chapters.[40]
In chapter seven of his Brāhmasphuṭasiddhānta, entitled Lunar Crescent, Brahmagupta rebuts the idea that the Moon is farther from the Earth than the Sun.[مطلوب توضيح] He does this by explaining the illumination of the Moon by the Sun.[41]
1. If the moon were above the sun, how would the power of waxing and waning, etc., be produced from calculation of the longitude of the moon? The near half would always be bright.
2. In the same way that the half seen by the sun of a pot standing in sunlight is bright, and the unseen half dark, so is [the illumination] of the moon [if it is] beneath the sun.
3. The brightness is increased in the direction of the sun. At the end of a bright [i.e. waxing] half-month, the near half is bright and the far half dark. Hence, the elevation of the horns [of the crescent can be derived] from calculation. [...][42]
He explains that since the Moon is closer to the Earth than the Sun, the degree of the illuminated part of the Moon depends on the relative positions of the Sun and the Moon, and this can be computed from the size of the angle between the two bodies.[41]
Further work exploring the longitudes of the planets, diurnal rotation, lunar and solar eclipses, risings and settings, the moon's crescent and conjunctions of the planets, are discussed in his treatise Khandakhadyaka.
انظر أيضاً
- Brahmagupta–Fibonacci identity
- Brahmagupta's formula
- Brahmagupta theorem
- Chakravala method
- List of Indian mathematicians
- History of science and technology in the Indian subcontinent
- آريابهاتا
- سيدانتا
- الفزاوي
- صيغة براهماگوپتا
- مبرهنة براهماگوپتا
المراجع
ملاحظات
الهامش
- ^ أ ب Pickover, Clifford (2008). Archimedes to Hawking: Laws of Science and the Great Minds Behind Them. Oxford University Press. p. 105. ISBN 978-0-19-979268-9.
- ^ أ ب Bose, Mainak Kumar (1988). Late classical India. A. Mukherjee & Co.[صفحة مطلوبة]
- ^ أ ب Sen, Amartya (2005). The Argumentative Indian. Allen Lane. p. 29. ISBN 978-0-7139-9687-6.
- ^ أ ب Thurston, Hugh (1993). Early Astronomy. New York: Springer-Verlag. ISBN 978-0-387-94107-3.[صفحة مطلوبة][المصدر لا يؤكد ذلك]
- ^ Bradley, Michael. The Birth of Mathematics: Ancient Times to 1300, p. 86 (Infobase Publishing 2006)
- ^ Mackenzie, Dana. The Universe in Zero Words: The Story of Mathematics as Told through Equations, p. 61 (Princeton University Press, 2012).
- ^ Sachau, Edward C. (1910), Alberuni's India, Volume I, London: Kegan Paul, Trench and Trubner, p. 153, https://archive.org/details/alberunisindiaac01biru/page/152/mode/2up, "Brahma-siddhānta, so-called from Brahman, composed by Brahmagupta, the son of Jishnu, from the town of Bhillamāla between Multān and Anhilwāra, 16 yojana from the latter place (?)"
- ^ Cai 2023, p. 114; Cooke 1997, p. 208
- ^ Ayyappappanikkar (1997). Medieval Indian Literature: Surveys and selections (in الإنجليزية). Sahitya Akademi. p. 493. ISBN 978-81-260-0365-5.
- ^ Bhattacharyya 2011, p. 185: "Brahmagupta, one of the most celebrated mathematicians of the East, indeed of the world, was born in the year 598 CE, in the town of Bhillamala during the reign of King Vyaghramukh of the Chapa Dynasty."
- ^ أ ب ت Gupta 2008, p. 162.
- ^ Bhattacharyya 2011, pp. 185–186.
- ^ Bose, Sen & Subbarayappa 1971.
- ^ أ ب ت ث Gupta 2008, p. 163.
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماة:0 - ^ Bhattacharyya 2011, p. 185.
- ^ Avari 2013, p. 32.
- ^ Young, M. J. L.; Latham, J. D.; Serjeant, R. B. (2 November 2006), Religion, Learning and Science in the 'Abbasid Period, Cambridge University Press, pp. 302–303, ISBN 978-0-521-02887-5, https://books.google.com/books?id=cJuDafHpk3oC&pg=PA302
- ^ van Bladel, Kevin (28 November 2014), "Eighth Century Indian Astronomy in the Two Cities of Peace", Islamic Cultures, Islamic Contexts: Essays in Honor of Professor Patricia Crone, BRILL, pp. 257–294, ISBN 978-90-04-28171-4
- ^ أ ب ت ث ج ح خ Plofker (2007, pp. 428–434)
- ^ أ ب Boyer (1991, "China and India" p. 221) "he was the first one to give a general solution of the linear Diophantine equation ax + by = c, where a, b, and c are integers. [...] It is greatly to the credit of Brahmagupta that he gave all integral solutions of the linear Diophantine equation, whereas Diophantus himself had been satisfied to give one particular solution of an indeterminate equation. Inasmuch as Brahmagupta used some of the same examples as Diophantus, we see again the likelihood of Greek influence in India – or the possibility that they both made use of a common source, possibly from Babylonia. It is interesting to note also that the algebra of Brahmagupta, like that of Diophantus, was syncopated. Addition was indicated by juxtaposition, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, as in our fractional notation but without the bar. The operations of multiplication and evolution (the taking of roots), as well as unknown quantities, were represented by abbreviations of appropriate words."
- ^ Brahmagupta; Bhāskara II (1817). Algebra, with Arithmetic and Mensuration, from the Sanscrit of Brahmegupta and Bháscara. Translated by Henry Thomas Colebrooke. John Murray. p. 319.
- ^ Tiwari, Sarju (1992), Mathematics in History, Culture, Philosophy, and Science: From Ancient Times to Modern Age, Mittal Publications, pp. 91–, ISBN 978-81-7099-404-6, https://books.google.com/books?id=-yyDJUD0DNwC&pg=PA91
- ^ Plofker (2007, pp. 422) The reader is apparently expected to be familiar with basic arithmetic operations as far as the square-root; Brahmagupta merely notes some points about applying them to fractions. The procedures for finding the cube and cube-root of an integer, however, are described (compared the latter to Aryabhata's very similar formulation). They are followed by rules for five types of combinations: [...]
- ^ أ ب ت ث ج ح Plofker (2007, pp. 421–427)
- ^ Plofker (2007, p. 423) Here the sums of the squares and cubes of the first n integers are defined in terms of the sum of the n integers itself;
- ^ Kaplan, Robert (1999). The Nothing That Is: A Natural History of Zero. London: Allen Lane/The Penguin Press. pp. 68–75. Bibcode:2000tnti.book.....K.
- ^ Boyer (1991, p. 220): However, here again Brahmagupta spoiled matters somewhat by asserting that 0 ÷ 0 = 0, and on the touchy matter of a ÷ 0, he did not commit himself.
- ^ أ ب Plofker (2007, p. 426)
- ^ Stillwell (2004, pp. 44–46): In the seventh century CE the Indian mathematician Brahmagupta gave a recurrence relation for generating solutions of x2 − Dy2 = 1, as we shall see in Chapter 5. The Indians called the Euclidean algorithm the "pulverizer" because it breaks numbers down to smaller and smaller pieces. To obtain a recurrence one has to know that a rectangle proportional to the original eventually recurs, a fact that was rigorously proved only in 1768 by Lagrange.
- ^ أ ب Stillwell (2004, pp. 72–74)
- ^ Plofker (2007, p. 424) Brahmagupta does not explicitly state that he is discussing only figures inscribed in circles, but it is implied by these rules for computing their circumradius.
- ^ Stillwell (2004, p. 77)
- ^ Plofker (2007, p. 427) After the geometry of plane figures, Brahmagupta discusses the computation of volumes and surface areas of solids (or empty spaces dug out of solids). His straightforward rules for the volumes of a rectangular prism and pyramid are followed by a more ambiguous one, which may refer to finding the average depth of a sequence of puts with different depths. The next formula apparently deals with the volume of a frustum of a square pyramid, where the "pragmatic" volume is the depth times the square of the mean of the edges of the top and bottom faces, while the "superficial" volume is the depth times their mean area.
- ^ Plofker (2007, p. 419)
- ^ Plofker (2007, pp. 419–420) Brahmagupta's sine table, like much other numerical data in Sanskrit treatises, is encoded mostly in concrete-number notation that uses names of objects to represent the digits of place-value numerals, starting with the least significant. [...]
There are fourteen Progenitors ("Manu") in Indian cosmology; "twins" of course stands for 2; the seven stars of Ursa Major (the "Sages") for 7, the four Vedas, and the four sides of the traditional dice used in gambling, for 6, and so on. Thus Brahmagupta enumerates his first six sine-values as 214, 427, 638, 846, 1051, 1251. (His remaining eighteen sines are 1446, 1635, 1817, 1991, 2156, 2312, 2459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, 3270). The Paitamahasiddhanta, however, specifies an initial sine-value of 225 (although the rest of its sine-table is lost), implying a trigonometric radius of R = 3438 approx= C(')/2π: a tradition followed, as we have seen, by Aryabhata. Nobody knows why Brahmagupta chose instead to normalize these values to R = 3270. - ^ Joseph (2000, pp.285–86).
- ^ أ ب Alberuni's India. London: Kegan Paul, Trench, Trübner & Co., 1910. Electronic reproduction. Vol. 1 and 2. New York: Columbia University Libraries, 2006. p. 272. Retrieved 3 June 2014.
- ^ Kitāb al-Jawharatayn al-'atīqatayn al-mā'i'atayn min al-ṣafrā' wa-al-bayḍā': al-dhahab wa-al-fiḍḍah كتاب الجوهرتين العتيقتين المائعتين من الصفراء والبيضاء : الذهب والفضة. Cairo: Maṭba'at Dār al-Kutub wa-al-Wathā'iq al-Qawmīyah bi-al-Qāhirah. 2004. pp. 43–44, 87. OCLC 607846741.
- ^ أ ب Plofker (2007, pp. 418–419)
- ^ أ ب Plofker (2007, pp. 419–420) Brahmagupta discusses the illumination of the moon by the sun, rebutting an idea maintained in scriptures: namely, that the moon is farther from the earth than the sun is. In fact, as he explains, because the moon is closer the extent of the illuminated portion of the moon depends on the relative positions of the moon and the sun, and can be computed from the size of the angular separation α between them.
- ^ Plofker (2007, p. 420)
المصادر
- مؤمن, عبد الأمير (2006). قاموس دار العلم الفلكي. بيروت، لبنان: دار العلم للملايين.
{{cite book}}: Cite has empty unknown parameter:|طبعة أولى coauthors=(help) - Plofker, Kim (2007). "Mathematics in India". The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. ISBN 9780691114859.
- Boyer, Carl B. (1991). A History of Mathematics (Second Edition ed.). John Wiley & Sons, Inc. ISBN 0471543977.
{{cite book}}:|edition=has extra text (help) - Cooke, Roger (1997). The History of Mathematics: A Brief Course. Wiley-Interscience. ISBN 0471180823.
- Stillwell, John (2004). Mathematics and its History (Second Edition ed.). Springer Science + Business Media Inc. ISBN 0387953361.
{{cite book}}:|edition=has extra text (help)
الهامش
وصلات خارجية
- Brahmagupta's Biography
- Brahmagupta's Brahma-sphuta-siddhanta English introduction, Sanskrit text, Sanskrit and Hindi commentaries (PDF)
- مقالات بالمعرفة بحاجة لذكر رقم الصفحة بالمصدر from March 2020
- مقالات ذات عبارات بحاجة لمصادر
- CS1 uses العربية-language script (ar)
- Short description is different from Wikidata
- Articles containing سنسكريتية-language text
- Articles containing إنگليزية-language text
- Pages using Lang-xx templates
- Articles with hatnote templates targeting a nonexistent page
- جميع الصفحات التي تحتاج تنظيف
- مقالات بالمعرفة تحتاج توضيح from November 2015
- CS1 errors: extra text: edition
- مواليد 598
- وفيات 668
- براهماگوپتا
- Medieval Indian mathematicians
- أشخاص من راجستان
- راجستاني (شعب)
- أشخاص من مقاطعة جالوره
- رياضياتيو القرن 7
- هنود القرن 7