حساب
الحساب Arithmetic هو فرع من الرياضيات (او اساس الرياضيات) ، وهو المعني بدراسة الخصائص الاساسية لتطبيق مجموعة من العمليات الحسابية على الاعداد ، ويعبر عنه في ادبيات الرياضيات بنظرية الاعداد.
العمليات الحسابية التقليدية هي الجمع والطرح والضرب والقسمة ، واحيانا كثيرة تجمل عمليات اخرى كالنسب المئوية ، الجذور التربيعية والاسس (الرفع إلى القوة كذا) ، والدوال اللوغارثمية تحت تسمية الحساب ، وتطبق العمليات الرياضية بحسب اولويات العمليات الحسابية والتي وبشكل عام تقدم عمليات الضرب والقسمة على عمليات الجمع والطرح.
التاريخ

العمليات الحسابية
مبرهنة الحساب الأساسية
The fundamental theorem of arithmetic states that any integer greater than 1 has a unique prime factorization (a representation of a number as the product of prime factors), excluding the order of the factors. For example, 252 only has one prime factorization:
- 252 = 22 × 32 × 71
Euclid's Elements first introduced this theorem, and gave a partial proof (which is called Euclid's lemma). The fundamental theorem of arithmetic was first proven by كارل فريدرش گاوس.
The fundamental theorem of arithmetic is one of the reasons why 1 is not considered a prime number. Other reasons include the sieve of Eratosthenes, and the definition of a prime number itself (a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers.).
الحساب العشري
Decimal representation refers exclusively, in common use, to the written numeral system employing arabic numerals as the digits for a radix 10 ("decimal") positional notation; however, any numeral system based on powers of 10, e.g., Greek, Cyrillic, Roman, or Chinese numerals may conceptually be described as "decimal notation" or "decimal representation".
Compound unit arithmetic
Compound[1] unit arithmetic is the application of arithmetic operations to mixed radix quantities such as feet and inches; gallons and pints; pounds, shillings and pence; and so on. Before decimal-based systems of money and units of measure, compound unit arithmetic was widely used in commerce and industry.
عمليات الحساب الأساسية
The techniques used in compound unit arithmetic were developed over many centuries and are well documented in many textbooks in many different languages.[2][3][4][5] In addition to the basic arithmetic functions encountered in decimal arithmetic, compound unit arithmetic employs three more functions:
- Reduction, in which a compound quantity is reduced to a single quantity—for example, conversion of a distance expressed in yards, feet and inches to one expressed in inches.[6]
- Expansion, the inverse function to reduction, is the conversion of a quantity that is expressed as a single unit of measure to a compound unit, such as expanding 24 oz to 1 lb 8 oz.
- Normalization is the conversion of a set of compound units to a standard form—for example, rewriting "1 ft 13 in" as "2 ft 1 in".
Knowledge of the relationship between the various units of measure, their multiples and their submultiples forms an essential part of compound unit arithmetic.
Principles of compound unit arithmetic
There are two basic approaches to compound unit arithmetic:
- Reduction–expansion method where all the compound unit variables are reduced to single unit variables, the calculation performed and the result expanded back to compound units. This approach is suited for automated calculations. A typical example is the handling of time by Microsoft Excel where all time intervals are processed internally as days and decimal fractions of a day.
- On-going normalization method in which each unit is treated separately and the problem is continuously normalized as the solution develops. This approach, which is widely described in classical texts, is best suited for manual calculations. An example of the ongoing normalization method as applied to addition is shown below.
| UK pre-decimal currency |
|---|
| 4 farthings (f) = 1 penny |
| 12 pennies (d) = 1 shilling |
| 20 shillings (s) = 1 pound (£) |
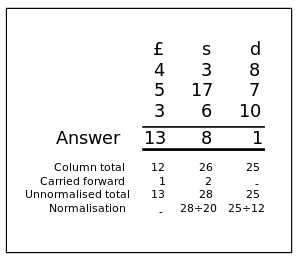
The addition operation is carried out from right to left; in this case, pence are processed first, then shillings followed by pounds. The numbers below the "answer line" are intermediate results.
The total in the pence column is 25. Since there are 12 pennies in a shilling, 25 is divided by 12 to give 2 with a remainder of 1. The value "1" is then written to the answer row and the value "2" carried forward to the shillings column. This operation is repeated using the values in the shillings column, with the additional step of adding the value that was carried forward from the pennies column. The intermediate total is divided by 20 as there are 20 shillings in a pound. The pound column is then processed, but as pounds are the largest unit that is being considered, no values are carried forward from the pounds column.
For the sake of simplicity, the example chosen did not have farthings.
العمليات في الممارسة
During the 19th and 20th centuries various aids were developed to aid the manipulation of compound units, particularly in commercial applications. The most common aids were mechanical tills which were adapted in countries such as the United Kingdom to accommodate pounds, shillings, pennies and farthings, and ready reckoners, which are books aimed at traders that catalogued the results of various routine calculations such as the percentages or multiples of various sums of money. One typical booklet[7] that ran to 150 pages tabulated multiples "from one to ten thousand at the various prices from one farthing to one pound".
The cumbersome nature of compound unit arithmetic has been recognized for many years—in 1586, the Flemish mathematician Simon Stevin published a small pamphlet called De Thiende ("the tenth")[8] in which he declared the universal introduction of decimal coinage, measures, and weights to be merely a question of time. In the modern era, many conversion programs, such as that included in the Microsoft Windows 7 operating system calculator, display compound units in a reduced decimal format rather than using an expanded format (e.g. "2.5 ft" is displayed rather than "2 ft 6 in").
نظرية الأعداد
Until the 19th century, number theory was a synonym of "arithmetic". The addressed problems were directly related to the basic operations and concerned primality, divisibility, and the solution of equations in integers, such as Fermat's last theorem. It appeared that most of these problems, although very elementary to state, are very difficult and may not be solved without very deep mathematics involving concepts and methods from many other branches of mathematics. This led to new branches of number theory such as analytic number theory, algebraic number theory, Diophantine geometry and arithmetic algebraic geometry. Wiles' proof of Fermat's Last Theorem is a typical example of the necessity of sophisticated methods, which go far beyond the classical methods of arithmetic, for solving problems that can be stated in elementary arithmetic.
الحساب في التعليم
Primary education in mathematics often places a strong focus on algorithms for the arithmetic of natural numbers, integers, fractions, and decimals (using the decimal place-value system). This study is sometimes known as algorism.
The difficulty and unmotivated appearance of these algorithms has long led educators to question this curriculum, advocating the early teaching of more central and intuitive mathematical ideas. One notable movement in this direction was the New Math of the 1960s and 1970s, which attempted to teach arithmetic in the spirit of axiomatic development from set theory, an echo of the prevailing trend in higher mathematics.[9]
Also, arithmetic was used by Islamic Scholars in order to teach application of the rulings related to Zakat and Irth. This was done in a book entitled The Best of Arithmetic by Abd-al-Fattah-al-Dumyati.[10]
The book begins with the foundations of mathematics and proceeds to its application in the later chapters.
انظر أيضاً
مواضيع ذات صلة
- Addition of natural numbers
- Additive inverse
- Arithmetic coding
- Arithmetic mean
- Arithmetic number
- Arithmetic progression
- Arithmetic properties
- Associativity
- Commutativity
- Distributivity
- Elementary arithmetic
- Finite field arithmetic
- Geometric progression
- Integer
- List of important publications in mathematics
- Mental calculation
- Number line
الهامش
- ^ Walkingame, Francis (1860). "The Tutor's Companion; or, Complete Practical Arithmetic" (PDF). Webb, Millington & Co. pp. 24–39. Archived from the original (PDF) on 2015-05-04.
- ^ Palaiseau, JFG (October 1816). Métrologie universelle, ancienne et moderne: ou rapport des poids et mesures des empires, royaumes, duchés et principautés des quatre parties du monde [Universal, ancient and modern metrology: or report of weights and measurements of empires, kingdoms, duchies and principalities of all parts of the world] (in الفرنسية). Bordeaux. Retrieved October 30, 2011.
- ^ Jacob de Gelder (1824). Allereerste Gronden der Cijferkunst [Introduction to Numeracy] (in الهولندية). 's-Gravenhage and Amsterdam: de Gebroeders van Cleef. pp. 163–176. Archived from the original on October 5, 2015. Retrieved March 2, 2011.
- ^ Malaisé, Ferdinand (1842). Theoretisch-Praktischer Unterricht im Rechnen für die niederen Classen der Regimentsschulen der Königl. Bayer. Infantrie und Cavalerie [Theoretical and practical instruction in arithmetic for the lower classes of the Royal Bavarian Infantry and Cavalry School] (in الألمانية). Munich. Archived from the original on 25 September 2012. Retrieved 20 March 2012.
- ^ Encyclopædia Britannica, I, Edinburgh, 1772, Arithmetick
- ^ Walkingame, Francis (1860). "The Tutor's Companion; or, Complete Practical Arithmetic" (PDF). Webb, Millington & Co. pp. 43–50. Archived from the original (PDF) on 2015-05-04.
- ^ Thomson, J (1824). The Ready Reckoner in miniature containing accurate table from one to the thousand at the various prices from one farthing to one pound. Montreal. Archived from the original on 28 July 2013. Retrieved 25 March 2012.
- ^ O'Connor, John J.; Robertson, Edmund F. (January 2004), "حساب", MacTutor History of Mathematics archive, University of St Andrews.
- ^ Mathematically Correct: Glossary of Terms
- ^ al-Dumyati, Abd-al-Fattah Bin Abd-al-Rahman al-Banna (1887). [[[:قالب:Wdl]] "The Best of Arithmetic"]. World Digital Library. Retrieved 30 June 2013.
{{cite web}}: Check|url=value (help)
المراجع
- Cunnington, Susan, The Story of Arithmetic: A Short History of Its Origin and Development, Swan Sonnenschein, London, 1904
- Dickson, Leonard Eugene, History of the Theory of Numbers (3 volumes), reprints: Carnegie Institute of Washington, Washington, 1932; Chelsea, New York, 1952, 1966
- Euler, Leonhard, Elements of Algebra, Tarquin Press, 2007
- Fine, Henry Burchard (1858–1928), The Number System of Algebra Treated Theoretically and Historically, Leach, Shewell & Sanborn, Boston, 1891
- Karpinski, Louis Charles (1878–1956), The History of Arithmetic, Rand McNally, Chicago, 1925; reprint: Russell & Russell, New York, 1965
- Ore, Øystein, Number Theory and Its History, McGraw–Hill, New York, 1948
- Weil, André, Number Theory: An Approach through History, Birkhauser, Boston, 1984; reviewed: Mathematical Reviews 85c:01004
وصلات خارجية
- MathWorld article about arithmetic
- The New Student's Reference Work/Arithmetic (historical)
- The Great Calculation According to the Indians, of Maximus Planudes – an early Western work on arithmetic at Convergence
- Weyde, P. H. Vander (1879). . The American Cyclopædia.
- CS1 الفرنسية-language sources (fr)
- CS1 الهولندية-language sources (nl)
- CS1 الألمانية-language sources (de)
- CS1 errors: URL
- Short description is different from Wikidata
- Articles with hatnote templates targeting a nonexistent page
- Portal-inline template with redlinked portals
- Pages with empty portal template
- Wikipedia articles incorporating a citation from The American Cyclopaedia
- Wikipedia articles incorporating a citation from The American Cyclopaedia with a Wikisource reference
- حساب
- تعليم الرياضيات