كرة ريمان
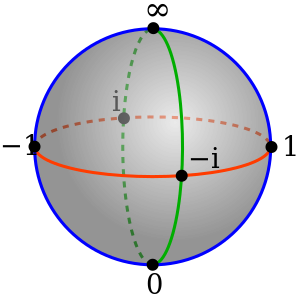
في الرياضيات ، كرة ريمان Riemann sphere ، على اسم الرياضي الشهير برنارد ريمان ، هي الطريقة الفريدة لإظهار السطح العقدي الممدد extended complex plane (السطح العقدي إضافة لنقطة في اللانهاية ) بحيث انه سيبدو من نقطة اللانهاية ممائلا لشكله عند أي عدد عقدي، بالذات بالنسبة للاستمرارية و الاشتقاقية. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value ∞ for infinity. With the Riemann model, the point "∞" is near to very large numbers, just as the point "0" is near to very small numbers.
The extended complex numbers are useful in complex analysis because they allow for division by zero in some circumstances, in a way that makes expressions such as well-behaved. For example, any rational function on the complex plane can be extended to a holomorphic function on the Riemann sphere, with the poles of the rational function mapping to infinity. More generally, any meromorphic function can be thought of as a holomorphic function whose codomain is the Riemann sphere.
In geometry, the Riemann sphere is the prototypical example of a Riemann surface, and is one of the simplest complex manifolds. In projective geometry, the sphere can be thought of as the complex projective line P1(C), the projective space of all complex lines in C2. As with any compact Riemann surface, the sphere may also be viewed as a projective algebraic curve, making it a fundamental example in algebraic geometry. It also finds utility in other disciplines that depend on analysis and geometry, such as the Bloch sphere of quantum mechanics and in other branches of physics.
The extended complex plane is also called closed complex plane.
الأعداد المركبة الممددة
The extended complex numbers consist of the complex numbers together with . The set of extended complex numbers may be written as , and is often denoted by adding some decoration to the letter , such as
The notation has also seen use, but as this notation is also used for the punctured plane , it can lead to ambiguity.[1]
Geometrically, the set of extended complex numbers is referred to as the Riemann sphere (أو extended complex plane).
العمليات الحسابية
Addition of complex numbers may be extended by defining, for ,
for any complex number , and multiplication may be defined by
for all nonzero complex numbers , with . Note that and are left undefined. Unlike the complex numbers, the extended complex numbers do not form a field, since does not have an additive nor multiplicative inverse. Nonetheless, it is customary to define division on by
for all nonzero complex numbers with and . The quotients and are left undefined.
الدوال الكسرية
Any rational function (in other words, is the ratio of polynomial functions and of with complex coefficients, such that and have no common factor) can be extended to a continuous function on the Riemann sphere. Specifically, if is a complex number such that the denominator is zero but the numerator is nonzero, then can be defined as . Moreover, can be defined as the limit of as , which may be finite or infinite.
The set of complex rational functions—whose mathematical symbol is —form all possible holomorphic functions from the Riemann sphere to itself, when it is viewed as a Riemann surface, except for the constant function taking the value everywhere. The functions of form an algebraic field, known as the field of rational functions on the sphere.
For example, given the function
we may define , since the denominator is zero at , and since as . Using these definitions, becomes a continuous function from the Riemann sphere to itself.
ككرة
The Riemann sphere can be visualized as the unit sphere in the three-dimensional real space . To this end, consider the stereographic projection from the unit sphere minus the point onto the plane which we identify with the complex plane by . In Cartesian coordinates and spherical coordinates on the sphere (with the zenith and the azimuth), the projection is
Similarly, stereographic projection from onto the plane identified with another copy of the complex plane by is written
The inverses of these two stereographic projections are maps from the complex plane to the sphere. The first inverse covers the sphere except the point , and the second covers the sphere except the point . The two complex planes, that are the domains of these maps, are identified differently with the plane , because an orientation-reversal is necessary to maintain consistent orientation on the sphere.
The transition maps between -coordinates and -coordinates are obtained by composing one projection with the inverse of the other. They turn out to be and , as described above. Thus the unit sphere is diffeomorphic to the Riemann sphere.
Under this diffeomorphism, the unit circle in the -chart, the unit circle in the -chart, and the equator of the unit sphere are all identified. The unit disk is identified with the southern hemisphere , while the unit disk is identified with the northern hemisphere .
Metric
A Riemann surface does not come equipped with any particular Riemannian metric. The Riemann surface's conformal structure does, however, determine a class of metrics: all those whose subordinate conformal structure is the given one. In more detail: The complex structure of the Riemann surface does uniquely determine a metric up to conformal equivalence. (Two metrics are said to be conformally equivalent if they differ by multiplication by a positive smooth function.) Conversely, any metric on an oriented surface uniquely determines a complex structure, which depends on the metric only up to conformal equivalence. Complex structures on an oriented surface are therefore in one-to-one correspondence with conformal classes of metrics on that surface.
Within a given conformal class, one can use conformal symmetry to find a representative metric with convenient properties. In particular, there is always a complete metric with constant curvature in any given conformal class.
In the case of the Riemann sphere, the Gauss–Bonnet theorem implies that a constant-curvature metric must have positive curvature . It follows that the metric must be isometric to the sphere of radius in via stereographic projection. In the -chart on the Riemann sphere, the metric with is given by
In real coordinates , the formula is
Up to a constant factor, this metric agrees with the standard Fubini–Study metric on complex projective space (of which the Riemann sphere is an example).
Up to scaling, this is the only metric on the sphere whose group of orientation-preserving isometries is 3-dimensional (and none is more than 3-dimensional); that group is called . In this sense, this is by far the most symmetric metric on the sphere. (The group of all isometries, known as , is also 3-dimensional, but unlike is not a connected space.)
Conversely, let denote the sphere (as an abstract smooth or topological manifold). By the uniformization theorem there exists a unique complex structure on up to conformal equivalence. It follows that any metric on is conformally equivalent to the round metric. All such metrics determine the same conformal geometry. The round metric is therefore not intrinsic to the Riemann sphere, since "roundness" is not an invariant of conformal geometry. The Riemann sphere is only a conformal manifold, not a Riemannian manifold. However, if one needs to do Riemannian geometry on the Riemann sphere, the round metric is a natural choice (with any fixed radius, though radius is the simplest and most common choice). That is because only a round metric on the Riemann sphere has its isometry group be a 3-dimensional group. (Namely, the group known as , a continuous ("Lie") group that is topologically the 3-dimensional projective space .)
Automorphisms
The study of any mathematical object is aided by an understanding of its group of automorphisms, meaning the maps from the object to itself that preserve the essential structure of the object. In the case of the Riemann sphere, an automorphism is an invertible biholomorphic map from the Riemann sphere to itself. It turns out that the only such maps are the Möbius transformations. These are functions of the form
where a, b, c, and d are complex numbers such that ad − bc ≠ 0. Examples of Möbius transformations include dilations, rotations, translations, and complex inversion. In fact, any Möbius transformation can be written as a composition of these.
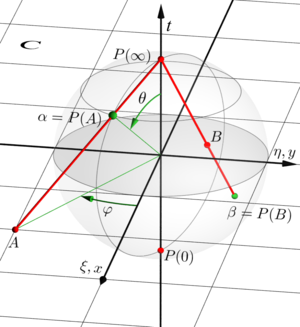
The Möbius transformations are homographies on the complex projective line. In projective coordinates, the transformation f can be written
Applications
In complex analysis, a meromorphic function on the complex plane (or on any Riemann surface, for that matter) is a ratio f/g of two holomorphic functions f and g. As a map to the complex numbers, it is undefined wherever g is zero. However, it induces a holomorphic map (f, g) to the complex projective line that is well-defined even where g = 0. This construction is helpful in the study of holomorphic and meromorphic functions. For example, on a compact Riemann surface there are no non-constant holomorphic maps to the complex numbers, but holomorphic maps to the complex projective line are abundant.
The Riemann sphere has many uses in physics. In quantum mechanics, points on the complex projective line are natural values for photon polarization states, spin states of massive particles of spin 1/2, and 2-state particles in general (see also Quantum bit and Bloch sphere). The Riemann sphere has been suggested as a relativistic model for the celestial sphere.[2] In string theory, the worldsheets of strings are Riemann surfaces, and the Riemann sphere, being the simplest Riemann surface, plays a significant role. It is also important in twistor theory.
انظر أيضاً
- هندسة امتثالية Conformal geometry
- Cross-ratio
- Dessin d'enfant
- Directed infinity
- Hopf bundle
- مستوى موبيوس
- Projectively extended real line
المراجع
- ^ "C^*". Archived from the original on October 8, 2021. Retrieved December 12, 2021.
- ^ R. Penrose (2007). The Road to Reality. Vintage books. pp. 428–430 (§18.5). ISBN 0-679-77631-1.
- Brown, James; Churchill, Ruel (1989). Complex Variables and Applications. New York: McGraw-Hill. ISBN 0-07-010905-2.
{{cite book}}: Unknown parameter|lastauthoramp=ignored (|name-list-style=suggested) (help) - Griffiths, Phillip; Harris, Joseph (1978). Principles of Algebraic Geometry. John Wiley & Sons. ISBN 0-471-32792-1.
{{cite book}}: Unknown parameter|lastauthoramp=ignored (|name-list-style=suggested) (help) - Penrose, Roger (2005). The Road to Reality. New York: Knopf. ISBN 0-679-45443-8.
- Rudin, Walter (1987). Real and Complex Analysis. New York: McGraw–Hill. ISBN 0-07-100276-6.
وصلات خارجية
- Hazewinkel, Michiel, ed. (2001), "Riemann sphere", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Moebius Transformations Revealed, by Douglas N. Arnold and Jonathan Rogness (a video by two University of Minnesota professors explaining and illustrating Möbius transformations using stereographic projection from a sphere)






































































![{\displaystyle [\zeta ,\ 1]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\ =\ [a\zeta +b,\ c\zeta +d]\ =\ \left[{\tfrac {a\zeta +b}{c\zeta +d}},\ 1\right]\ =\ [f(\zeta ),\ 1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15daa3dc6b0cede51b0d2722da054b8dea8f0562)