تأثير كهروحراري
| التأثير الكهروحراري |
|---|
 |
التأثير الكهروحراري (إنگليزية: thermoelectric effect)، هو تحويل مباشر لاختلافات درجات الحرارة إلى جهد كهربائي والعكس.
تأثير پلتييه (Peltier effect) وتأثير طومسون (Thomson effect) ظاهرتان حراريتان كهربائيتان تستخدمان في القياسات الحرارية وفي تحقيق تحولات عكوسة بين الطاقة الحرارية والطاقة الكهربائية.
إن تحويل الحرارة مباشرة إلى طاقة كهربائية تحويلاً عكوساً يتم بثلاث ظواهر مترابطة هي: تأثير سيبِك (Seebeck effect) وتأثير پلْتِييه وتأثير طومسون. أما تأثير سيبك فيتعلق بتولد قوة محركة كهربائية (ق.م.ك) في دارة كهربائية مكونة من ناقلين مختلفين جُعلت وُصلتاهما في درجتيْ حرارة مختلفتين. وأما تأثير بلتيه فيرتبط بالحرارة المتولدة أو الممتصة في وصلة ناقلين مختلفين عندما يمر تيار كهربائي مستمر في هذه الوصلة. وأما تأثير طومسون فيتصل بتولد الحرارة أو امتصاصها في ناقل وحيد يمر فيه تيار مستمر وتتدرج فيه درجة الحرارة تدرجاً منتظماً.
وتعرَّف هذه التآثير الكهرحرارية الثلاثة بدلالة معاملاتها: معامل الاستطاعة الكهرحرارية س ومعامل بلتيه بل ومعامل طومسون ط وذلك من أجل ناقل متجانس في درجة حرارة ثابتة. وترتبط هذه المعاملات بعضها مع بعض بعلاقات كلفن Kelvin التي تؤدي معرفة معلومات كاملة عن أحد لمعاملات فيها إلى معلومات كاملة عن الثلاثة معاً. لذلك يُكتفى بقياس أحدها وهو عادة ، إذ يَسْهل قياسه بدقة كبيرة. والاِرتباطات بين معامل طومسون ومعامل پلتييه ومعامل سيبِك كلها متجمـّعة فيما يـُعرف بـ«علاقة طومسون الأولى»:
بما فيها درجة الحرارة المطلقة للموصّل (conductor) ، معامل طومسون ، معامل پلتييه و معامل سيبِك (أنظر تحت للحصول على التفاصيل).
تأثير طومسون
عندما يمر تيار كهربائي في ناقل درجة حرارته ثابتة فإنه تتولد فيه حرارة تتناسب مع مربع شدة التيار، أي أنها لاتتوقف على جهة التيار، وتعرف هذه الظاهرة بتأثير (مفعول) جول (Joule effect) وهي ظاهرة لاعكوسة. في عام 1854 حاول وليم طومسون (لورد كلفن) تفسير الاختلاف بين نتائج قياس هذه الحرارة تجريبياً وما تعطيه الدراسة الترمودينامية النظرية،فافترض للتوفيق بينها وجود حرارة إضافية تتولد تولداً عكوساً حين يكون هناك تدرَّج في درجة حرارة الناقل دْ، وسميت هذه الحرارة «حرارة طومسون» وهي عكوسة، أي أن الناقل ينقلب من ناشرٍ للحرارة إلى ماص لها عندما تتغير جهة التيار أو جهة تدرَّج الحرارة (ولكن ليس إذا تم عكسها معاً في آن واحد). إن تدرُّج درجة الحرارة في الناقل المعدني الواحد ينجم عنه فرق كمون (potential difference) بين طرفيْ هذا الناقل يُعزى إلى تولد قوة محركة كهربائية منشؤها هذا التدرج. ولكن هذه القوى المحركة الكهربائية ذات قيم ضئيلة فهي +2.2 مكروفلط/دْ في النحاس و(-8.4) مكروفلط/دْ في الحديد (المكرو = 10-6) وهي لاتولد تياراً كهربائياً في دارة مؤلفة من ناقل واحد، ولكن إذا كان هناك تدرج حراري في هذا الناقل ومر فيه تيار مستمر فإنه يضاف إلى حرارة جول حرارة عكوسة ناشئة عن تأثير طومسون، وهي ذات قيمة ضئيلة جداً ويصعب قياسها.
In different materials, the Seebeck coefficient is not constant in temperature, and so a spatial gradient in temperature can result in a gradient in the Seebeck coefficient. If a current is driven through this gradient, then a continuous version of the Peltier effect will occur. This Thomson effect was predicted and later observed in 1851 by Lord Kelvin (William Thomson).[1] It describes the heating or cooling of a current-carrying conductor with a temperature gradient.
If a current density is passed through a homogeneous conductor, the Thomson effect predicts a heat production rate per unit volume
where is the temperature gradient, and is the Thomson coefficient. The Thomson coefficient is related to the Seebeck coefficient as (see below). This equation, however, neglects Joule heating and ordinary thermal conductivity (see full equations below)
تأثير پلتييه
تمهيد لتأثير پلتييه
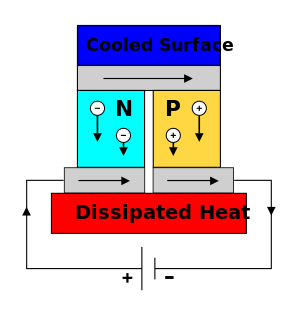
هو ظاهرة اكتشفها عام 1834 العالم جان شارل أثناس پلتييه، إذ لاحظ أنه عند إمرار تيار كهربائي مستمر في وُصْلة سلكين معدنيين مختلفين تنخفض درجة حرارة الوصلة أو ترتفع تبعاً لجهة التيار فيها. فإذا مر تيار كهربائي مستمر في دارة كهربائية مكوَّنة من وصلتين لسلكين مختلفين فإن إحدى الوصلتين تبرد والأخرى تسخن. فأثر بلتيه هو إذن ظاهرة عكوسة كتأثير طومسون بخلاف أثر جول الحراري غير العكوس.[2]
وقد استُعملت في دراسة تأثير بلتيه أزواج مختلفة من المعادن (حديد - نحاس) و(بزموت - نحاس)، ودلت التجارب على أن قوةً محركة كهربائية تتولد عن الوصلة وجهتها من البزموت إلى النحاس وسُميت هذه القوة « قوة بلتيه» .
معامل پلتييه
يعرّف معامل پلتيه (Peltier coefficient) بل ب جـ بأنه كمية التي تتعلق بتدفق الطاقة الحرارية المتولدة أو الممتصة في وصلة المادتين ب (من الموصـّل A) و جـ (من الموصـّل B) من جراء مرور شحنة كهربائية في الوصلة مقدارها كولون واحد.
حيث أنّ و يعتبران معاملان تبع پلتييه من الموصـّلان A و B ، و يعتبر التيار الكهربائي (من A إلى B).
ونظراً لصغر كمية الحرارة التي تصاحب أثر بلتيه وللتعقيدات الناجمة عن وجود تأثير جول الحراري وتأثير طمسون، فإن من الصعب قياس معامل بلتيه قياساً دقيقاً، لذلك يُحسب هذا المعامل عادة من علاقات كلفن التي سبق ذكرها باستعمال القيم التجريبية للمعامل س ب جـ وقد دلت التجارب على أن معامل بلتيه مستقل عن شدة التيار وعن شكل الأسلاك الناقلة، ولايتوقف إلا على طبيعة المادتين ب، وجـ وعلى درجة حرارة الوصلة.
ممارسات ومواد
وقد استُفيد من تأثير پلتييه في التبريد الكهرحراري الذي طُبِّق منذ عام 1960 باستعمال الشــِـبـْهمـُوَصـِّـلَات (semiconductors) التي اكتشف فيها هذا التأثير، وبخاصة في المادة بزموت-تلوريد (bismuth-telluride) التي تتميز بناقلية حراية ضعيفة مقارنة بالمعادن، وبقيمة معامل بلتيه الكبيرة التي تبلغ 120 ملّي فلط، في حين أنها 3 ملي فلط من أجل الوصلة « حديد - نحاس» ، و21 ملي فلط من أجل الوصلة « بزموت - نحاس» . ويتألف جهاز التبريد من صفيحة معدنية متصلة بسلسلة متناوبة من وصلتين من بزموت-تلوريد، إحداهما من النوع السالب والأخرى من النوع الموجب بحيث تُمتص الحرارة عند الجانب الذي يراد تبريده بينما تنتشر الحرارة في الجانب الآخر. ويمكن قلب الجهاز إلى أداة تدفئة بعكس جهة التيار. وعلى الرغم من أن البرّاد الذي يعمل بتأثير بلتيه لايضاهي البراد العادي تجارياً إلا أنه يفضّل استخدامه في أحوال خاصة مثل الرحلات الفضائية لصغر حجمه وخفة وزنه واعتماده على حركة الحرارة والكهرباء بدلاً من المحركات في البرادات الشائعة الاستعمال.
تأثير زيبِك
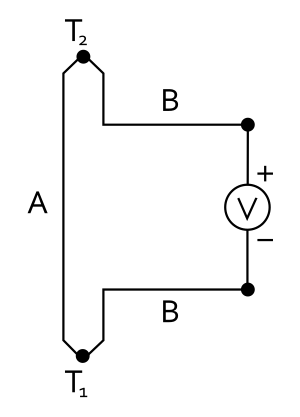
عن فرق من درجتين حراريتين في نقطتين لللَمـْس كلاهنا من قطعتين موصـّلتين من مادّتين مختلفتين A و B يـُسـْفـِـر جهد كهربائي على أساس تأثير سيبِك المنسوب للفزيائي الألماني توماس يوهان سيبك (Thomas Johann Seebeck) بمقدار
في دارة كهربائية.
المعاملان تبع سيبك و كلاهما ثابتان مادّيـّتان الذان يتعلقان بدرجة الحرارة. المعامل تبع سيبك له بـُعد من جهد كهربائي نسبة ً لكلّ فرق من درجتين من الحرارة (Volt/Kelvin) . القيم النمطية في هذا الاِرتباط تقع في حدود عند الفــِـلـُـزَات (metals) أثناء درجات من الحرارة بالقرب إلى . عند فرقات صغيرة من الدرجتين من الحرارة وثبوت المعاملتين تبع سيبك يـُـسـْمـَـح بـاِستعمال التبسيط التالي :
في الصيغة التقريبية من الجهد الكهروحراري لم تأتي هذه الكمـّيـّة إلا بصياغة بإبراز فرق من معاملَين تبع سيبك ، بسبب أنّ معلملات مفردة لسيبك لا تتم إيجادها إلا بصعوبات (أنظر تأثير طومسون) . ولذلك صار پلاتين العنصر الكيميائي المرجعي ليكون أحد المادّتين عندما يـُـقاس الجهد الكهروحراري بشكل منتظم ، وقيم مـُرَصـَّـة في جداول من متتاليات الجهد الكهروحراري أحياناً كثيراً تكون مبنية على أنّ الپلاتين يكن أحد المادّتين المستعملة.
تأثير سيبِك يصف إسفار الجهد المذكور فقط. دارات كهربائية من الحول موصـَّلة ببناء هذا الاِختبار ، وبخاصـّة تدفـّق تيـّار من أجلها ، هي لم تعبـّر عن تأثير سيبك ، بل تعتبر ظواهر متابعة لقانون أوم.
المعادلات الكهروحرارية الكاملة
Often, more than one of the above effects is involved in the operation of a real thermoelectric device. The Seebeck effect, Peltier effect, and Thomson effect can be gathered together in a consistent and rigorous way, described here; this also includes the effects of Joule heating and ordinary heat conduction. As stated above, the Seebeck effect generates an electromotive force, leading to the current equation[3]
To describe the Peltier and Thomson effects, we must consider the flow of energy. If temperature and charge change with time, the full thermoelectric equation for the energy accumulation, , is[3]
where is the thermal conductivity. The first term is the Fourier's heat conduction law, and the second term shows the energy carried by currents. The third term, , is the heat added from an external source (if applicable).
If the material has reached a steady state, the charge and temperature distributions are stable, so and . Using these facts and the second Thomson relation (see below), the heat equation can be simplified to
The middle term is the Joule heating, and the last term includes both Peltier ( at junction) and Thomson ( in thermal gradient) effects. Combined with the Seebeck equation for , this can be used to solve for the steady-state voltage and temperature profiles in a complicated system.
If the material is not in a steady state, a complete description needs to include dynamic effects such as relating to electrical capacitance, inductance and heat capacity.
علاقات طومسون
In 1854, Lord Kelvin found relationships between the three coefficients, implying that the Thomson, Peltier, and Seebeck effects are different manifestations of one effect (uniquely characterized by the Seebeck coefficient).[4]
The first Thomson relation is[3]
where is the absolute temperature, is the Thomson coefficient, is the Peltier coefficient, and is the Seebeck coefficient. This relationship is easily shown given that the Thomson effect is a continuous version of the Peltier effect. Using the second relation (described next), the first Thomson relation becomes .
The second Thomson relation is
This relation expresses a subtle and fundamental connection between the Peltier and Seebeck effects. It was not satisfactorily proven until the advent of the Onsager relations, and it is worth noting that this second Thomson relation is only guaranteed for a time-reversal symmetric material; if the material is placed in a magnetic field or is itself magnetically ordered (ferromagnetic, antiferromagnetic, etc.), then the second Thomson relation does not take the simple form shown here.[5]
The Thomson coefficient is unique among the three main thermoelectric coefficients because it is the only one directly measurable for individual materials. The Peltier and Seebeck coefficients can only be easily determined for pairs of materials; hence, it is difficult to find values of absolute Seebeck or Peltier coefficients for an individual material.
If the Thomson coefficient of a material is measured over a wide temperature range, it can be integrated using the Thomson relations to determine the absolute values for the Peltier and Seebeck coefficients. This needs to be done only for one material, since the other values can be determined by measuring pairwise Seebeck coefficients in thermocouples containing the reference material and then adding back the absolute Seebeck coefficient of the reference material. For more details on absolute Seebeck coefficient determination, see Seebeck coefficient.
التطبيقات
المولدات الكهروحرارية
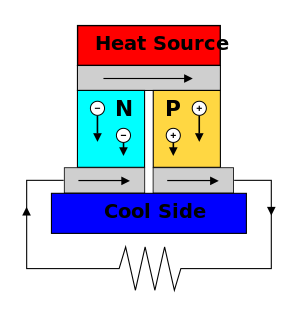
The Seebeck effect is used in thermoelectric generators, which function like heat engines, but are less bulky, have no moving parts, and are typically more expensive and less efficient. They have a use in power plants for converting waste heat into additional electrical power (a form of energy recycling) and in automobiles as automotive thermoelectric generators (ATGs) for increasing fuel efficiency. Space probes often use radioisotope thermoelectric generators with the same mechanism but using radioisotopes to generate the required heat difference. Recent uses include stove fans,[6] lighting powered by body heat[7] and a smartwatch powered by body heat.[8]
تأثير پلتييه
The Peltier effect can be used to create a refrigerator that is compact and has no circulating fluid or moving parts. Such refrigerators are useful in applications where their advantages outweigh the disadvantage of their very low efficiency. The Peltier effect is also used by many thermal cyclers, laboratory devices used to amplify DNA by the polymerase chain reaction (PCR). PCR requires the cyclic heating and cooling of samples to specified temperatures. The inclusion of many thermocouples in a small space enables many samples to be amplified in parallel.
قياس درجة الحرارة
Thermocouples and thermopiles are devices that use the Seebeck effect to measure the temperature difference between two objects. Thermocouples are often used to measure high temperatures, holding the temperature of one junction constant or measuring it independently (cold junction compensation). Thermopiles use many thermocouples electrically connected in series, for sensitive measurements of very small temperature difference.
انظر أيضاً
- Heat transfer
- قوانين جول
- Pyroelectricity - the creation of an electric field in a crystal after uniform heating
- إلكترونيات سپينية
- Thermionic emission
- Thermoacoustic refrigeration
- Thermodiffusion
- Thermoelectric cooling
- Thermoelectricity
- Thermogenerator
- عمود حراري
- طاقة حرارية
المصادر
- ^ Thomson, William (1851). "On a mechanical theory of thermo-electric currents". Proceedings of the Royal Society of Edinburgh. 3 (42): 91–98.
- ^ Peltier (1834). "Nouvelles expériences sur la caloricité des courants électrique" [New experiments on the heat effects of electric currents]. Annales de Chimie et de Physique (in French). 56: 371–386.
{{cite journal}}: CS1 maint: unrecognized language (link) - ^ أ ب ت "A.11 Thermoelectric effects". Eng.fsu.edu. 2002-02-01. Retrieved 2013-04-22.
- ^ Thomson, William (1854). "On the dynamical theory of heat. Part V. Thermo-electric currents". Transactions of the Royal Society of Edinburgh. 21: 123–171.
- ^ There is a generalized second Thomson relation relating anisotropic Peltier and Seebeck coefficients with reversed magnetic field and magnetic order. See, for example, Rowe, D. M., ed. (2010). Thermoelectrics Handbook: Macro to Nano. CRC Press. ISBN 9781420038903.
- ^ "TEG Module and Seebeck Effect". StoveFanReviews.com.
- ^ Goodner, Stanley (October 16, 2015). "Powered by body heat, Lumen flashlight never needs batteries". Gizmag.
- ^ Signe Brewster (November 16, 2016). "Body Heat Powers This Smart Watch; The Matrix PowerWatch is a FitBit competitor that exploits the temperature difference between your skin and the air for power". MIT Technology Review. Retrieved 7 October 2019.
- Besançon, Robert M. (1985). The Encyclopedia of Physics, Third Edition. Van Nostrand Reinhold Company. ISBN 0-442-25778-3.
- Rowe, D. M., ed. (2006). Thermoelectrics Handbook:Macro to Nano. Taylor & Francis. ISBN 0-8493-2264-2.
- Ioffe, A.F. (1957). Semiconductor Thermoelements and Thermoelectric Cooling. Infosearch Limited. ISBN 0-8508-6039-3.
- Thomson, William (1851). "On a mechanical theory of thermoelectric currents". Proc.Roy.Soc.Edinburgh: 91–98.
وصلات خارجية
عامة
- Device to measure the Seebeck Effect
- Thomson Effect - Interactive Java Tutorial National High Magnetic Field Laboratory
- International Thermoelectric Society
- Thermoelectric News
- General
- Explanation of carrier diffusion and phonon drag components of thermopower
- Good explanation of thermo-electric cooler design
- BSST Technical Papers on thermoelectric devices
- Gizmag Article on application of Thermoelectrics