علم الحاسوب النظري
Theoretical computer science(s) (TCS) are divisions or subsets of general computer science and focus on more abstract and mathematical aspects of computing.
These divisions and subsets include analysis of algorithms and formal semantics of programming languages. Technically, there are hundreds of divisions and subsets besides these two. Each of the multiple parts have their own individual personal leaders (of popularity) and there are many associations and professional social groups and publications of distinction.
Scope
It is not easy to circumscribe the theory areas precisely; the ACM's Special Interest Group on Algorithms and Computation Theory (SIGACT), which describes its mission as the promotion of theoretical computer science, says:[1]
The field of theoretical computer science is interpreted broadly so as to include algorithms, data structures, computational complexity theory, distributed computation, parallel computation, VLSI, machine learning, computational biology, computational geometry, information theory, cryptography, quantum computation, computational number theory and algebra, program semantics and verification, automata theory, and the study of randomness. Work in this field is often distinguished by its emphasis on mathematical technique and rigor.
To this list, the ACM's journal Transactions on Computation Theory adds coding theory, computational learning theory, and theoretical computer science aspects of areas such as databases, information retrieval, economic models and networks.[2] Despite this broad scope, the "theory people" in computer science self-identify as different. Some characterize themselves as doing the "'science' underlying the field of computing,"[3] although this neglects the experimental science done in non-theoretical areas such as software system research.
|
|
| |
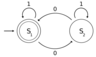
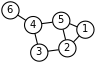
| Mathematical logic | Automata theory | Number theory | Graph theory |
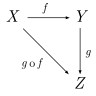
|

|
| |
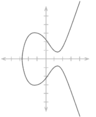
| Type theory | Category theory | Computational geometry | Quantum computing theory |
History
While formal algorithms have existed for millennia (Euclid's algorithm for determining the greatest common divisor of two numbers is still used in computation), it was not until 1936 that Alan Turing, Alonzo Church and Stephen Kleene formalized the definition of an algorithm in terms of computation. While binary and logical systems of mathematics had existed before 1703, when Gottfried Leibniz formalized logic with binary values for true and false. While logical inference and mathematical proof had existed in ancient times, in 1931 Kurt Gödel proved with his incompleteness theorem that there were fundamental limitations on what statements, even if true, could be proved.
These developments have led to the modern study of logic and computability, and indeed the field of theoretical computer science as a whole. Information theory was added to the field with a 1948 theory of the statistical mechanics of information by Claude Shannon. In the same decade, Donald Hebb introduced a mathematical model of learning in the brain. With mounting biological data supporting this hypothesis with some modification, the fields of neural networks and parallel distributed processing were established.
With the development of quantum mechanics in the beginning of the 20th century came the concept that mathematical operations could be performed on an entire particle wavefunction. In other words, one could compute functions on multiple states simultaneously. This led to the concept of a quantum computer in the latter half of the 20th century that took off in the 1990s when Peter Shor showed that such methods could be used to factor large numbers in polynomial time, which, if implemented, would render most modern public key cryptography systems uselessly insecure.
Modern theoretical computer science research is based on these basic developments, but includes many other mathematical and interdisciplinary problems that have been posed.
Organizations
Journals and newsletters
- Information and Computation
- Theory of Computing (open access journal)
- Formal Aspects of Computing
- Journal of the ACM
- SIAM Journal on Computing (SICOMP)
- SIGACT News
- Theoretical Computer Science
- Theory of Computings Systems
- International Journal of Foundations of Computer Science
- Chicago Journal of Theoretical Computer Science (open access journal)
- Foundations and Trends in Theoretical Computer Science
- Journal of Automata, Languages and Combinatorics
- Acta Informatica
- Fundamenta Informaticae
- ACM Transactions on Computation Theory
- ACM Transactions on Algorithms
- Information Processing Letters
Conferences
- Annual ACM Symposium on Theory of Computing (STOC) [4]
- Annual IEEE Symposium on Foundations of Computer Science (FOCS) [4]
- ACM–SIAM Symposium on Discrete Algorithms (SODA) [4]
- Annual ACM Symposium on Computational Geometry (SoCG) [5]
- International Colloquium on Automata, Languages and Programming (ICALP) [5]
- Symposium on Theoretical Aspects of Computer Science (STACS) [5]
- European Symposium on Algorithms (ESA) [5]
- IEEE Symposium on Logic in Computer Science (LICS) [4]
- International Symposium on Algorithms and Computation (ISAAC) [5]
- Workshop on Approximation Algorithms for Combinatorial Optimization Problems (APPROX) [5]
- Workshop on Randomization and Computation (RANDOM) [5]
- Computational Complexity Conference (CCC) [5]
- ACM Symposium on Parallelism in Algorithms and Architectures (SPAA) [5]
- ACM Symposium on Principles of Distributed Computing (PODC) [4]
انظر أيضاً
- Formal science
- Unsolved problems in computer science
- List of important publications in theoretical computer science
Notes
- ^ "SIGACT". Retrieved 2009-03-29.
- ^ "ToCT". Retrieved 2010-06-09.
- ^ "Challenges for Theoretical Computer Science: Theory as the Scientific Foundation of Computing". Retrieved 2009-03-29.
- ^ أ ب ت ث ج The 2007 Australian Ranking of ICT Conferences: tier A+.
- ^ أ ب ت ث ج ح خ د ذ The 2007 Australian Ranking of ICT Conferences: tier A.
Further reading
- Martin Davis, Ron Sigal, Elaine J. Weyuker, Computability, complexity, and languages: fundamentals of theoretical computer science, 2nd ed., Academic Press, 1994, ISBN 0122063821. Covers theory of computation, but also program semantics and quantification theory. Aimed at graduate students.

