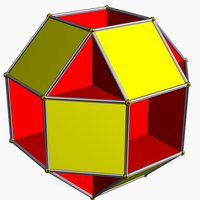
ضد متوازي الأضلاع

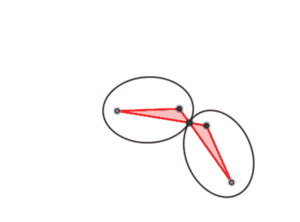
ضد متوازي الأضلاع Antiparallelogram هو رباعي أضلاع يكون فيه كل ضلعين غير متجاورين متطابقين، ويكون (على عكس متوازي الأضلاع) يكون كل زوج من الأضلاع المتقابلة متقاطعان.

ضد متوازي الأضلاع

إذا كان طول ضلعين متجاورين يحققان النسبة ${\sqrt {2}}:1$ فيكون مركز الضلعين المتقابلين يشكلان شكل رمز اللانهاية.

An antiparallelogram is a special case of a crossed quadrilateral, which has generally unequal edges. A special form of the antiparallelogram is a crossed rectangle, in which two opposite edges are parallel.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الخصائص

Every antiparallelogram has an axis of symmetry through its crossing point. Because of this symmetry, it has two pairs of equal angles as well as two pairs of equal sides. Together with the kites and the isosceles trapezoids, antiparallelograms form one of three basic classes of quadrilaterals with a symmetry axis. The convex hull of an antiparallelogram is an isosceles trapezoid, and every antiparallelogram may be formed from the non-parallel sides (or either pair of parallel sides in case of a rectangle) and diagonals of an isosceles trapezoid.

Every antiparallelogram is a cyclic quadrilateral, meaning that its four vertices all lie على دائرة واحدة.

 في متعددات الأسطح

The small rhombihexahedron. Slicing off any vertex of this shape gives an anti­parallelogram cross-section as the vertex figure.

The small rhombihexacron, a polyhedron with anti­parallelograms (formed by pairs of coplanar triangles) as its faces.

Several nonconvex uniform polyhedra, including the tetrahemihexahedron, cubohemioctahedron, octahemioctahedron, small rhombihexahedron, small icosihemidodecahedron, and small dodecahemidodecahedron, have antiparallelograms as their vertex figures, the cross-sections formed by slicing the polyhedron by a plane that passes near a vertex, perpendicularly to the axis between the vertex and the center.

For uniform polyhedra of this type in which the faces do not pass through the center point of the polyhedron, the dual polyhedron has antiparallelograms as its faces; examples of dual uniform polyhedra with antiparallelogram faces include the small rhombihexacron, the great rhombihexacron, the small rhombidodecacron, the great rhombidodecacron, the small dodecicosacron, and the great dodecicosacron. The antiparallelograms that form the faces of these dual uniform polyhedra are the same antiparallelograms that form the vertex figure of the original uniform polyhedron.

Bricard octahedron constructed as a double pyramid over an anti­parallelogram.

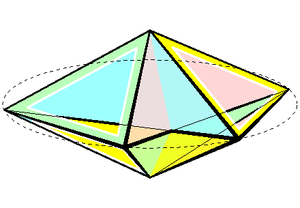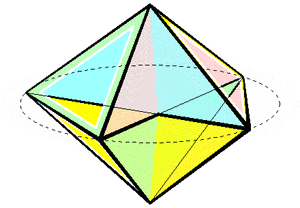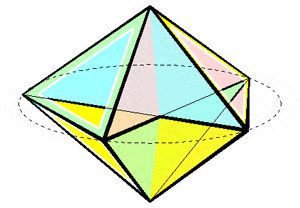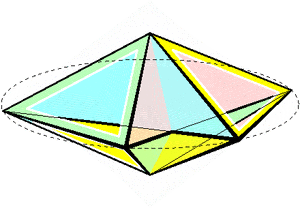
One form of a non-uniform but flexible polyhedron, the Bricard octahedron, can be constructed as a double pyramid over an antiparallelogram.

 Four-bar linkages

The antiparallelogram has been used as a form of four-bar linkage, in which four rigid beams of fixed length (the four sides of the antiparallelogram) may rotate with respect to each other at joints placed at the four vertices of the antiparallelogram. In this context it is also called a butterfly or bow-tie linkage. As a linkage, it has a point of instability in which it can be converted into a parallelogram and vice versa.

Fixing the short edge of an anti­parallelogram linkage causes the crossing point to trace out an ellipse.

 الميكانيكا السماوية

In the n-body problem, the study of the motions of point masses under Newton's law of universal gravitation, an important role is played by central configurations, solutions to the n-body problem in which all of the bodies rotate around some central point as if they were rigidly connected to each other. For instance, for three bodies, there are five solutions of this type, given by the five Lagrangian points. For four bodies, with two pairs of the bodies having equal masses (but with the ratio between the masses of the two pairs varying continuously), numerical evidence indicates that there exists a continuous family of central configurations, related to each other by the motion of an antiparallelogram linkage.