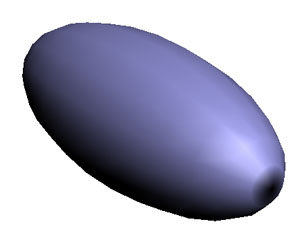
سطح ناقص
في الهندسة الرياضية، السطح الناقص أو السطح الإهليلجي (Ellipsoid) هو أحد السطوح الثنائية في فضاء ثلاثي الأبعاد، كما يمكن إطلاقه على مماثلاته في فضاءات أكثر بعدا. معادلة السطح الناقص العامة تكون على النحو التالي:
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle {x^2 \over a^2}+{y^2 \over b^2}+{z^2 \over c^2}=1 }
حيث a وb وc أرقام حقيقة موجبة تحدد شكل وأبعاد السطح الناقص. إذا تساوى رقمان من هذه الأرقام فإن الشكل الناتج شبه كرة وأما إذا تساوت الأرقام الثلاثة فإن الشكل الناتج هو كرة.
لو افترضنا أن a ≥ b ≥ c، إذن ينتج عندما:
- a ≠ b ≠ c سطحا ناقصا مختلف الأطوال.
- c = 0 قطعا ناقصا.
- c > a = b شبه الكرة المتطاول.
- c < a = b شبه الكرة المفلطح.
- b = a = c كرة
بالإمكان قياس حجم أي سطح ناقصي عن طريق:
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{3} \pi abc}
انظر أيضا
This article contains content from Wikimedia licensed under CC BY-SA 4.0. Please comply with the license terms.