توازي (هندسة)

هذا المقال هو عن علاقة رياضية بين الخطوط. إذا كنت تريد الاستخدامات الأخرى، انظر متوازي (توضيح).

"خطوط متوازية" redirects here. For other uses, see خطوط متوازية (توضيح).

رسم فن خطي لخطوط ومنحنيات متوازية.

في الهندسة الرياضية، يعبر التوازي عن علاقة ثنائية بين كائنين هندسيين مثل خطين مستقيمين أو مستويين، و تشترط هذه العلاقة استحالة التقاء هذين الكائنين في جميع نقاط الفضاء. يرمز لعملية التوازي بخطين عموديين متوازيين بالشكل ABC||DEF.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الرمز

المقالة الرئيسية: Parallel operator

The parallel symbol is $\parallel$. For example, $AB\parallel CD$ indicates that line AB is parallel to line CD.

In the Unicode character set, the "parallel" and "not parallel" signs have codepoints U+2225 (∥) and U+2226 (∦), respectively. In addition, U+22D5 (⋕) represents the relation "equal and parallel to".

 التوازي الإقليدي

 خطان في مستوى

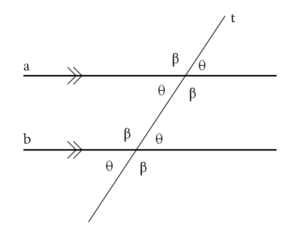
 شروط التوازي

المستقيمان a و b هما مستقيمان متوازيان. This can be proved because the transversal t produces congruent corresponding angles $\theta$, shown here both to the right of the transversal, one above and adjacent to line a and the other above and adjacent to line b.

 Construction

The three properties above lead to three different methods of construction of parallel lines.

The problem: Draw a line through a parallel to l.

• 

  Property 1: Line m has everywhere the same distance to line l.

• 

  Property 2: Take a random line through a that intersects l in x. Move point x to infinity.

• 

  Property 3: Both l and m share a transversal line through a that intersect them at 90°.

 Distance between two parallel lines

المقالة الرئيسية: Distance between two lines

Because parallel lines in a Euclidean plane are equidistant there is a unique distance between the two parallel lines. Given the equations of two non-vertical, non-horizontal parallel lines,

$y=mx+b_{1}\,$

$y=mx+b_{2}\,,$

the distance between the two lines can be found by locating two points (one on each line) that lie on a common perpendicular to the parallel lines and calculating the distance between them. Since the lines have slope m, a common perpendicular would have slope −1/m and we can take the line with equation y = −x/m as a common perpendicular. Solve the linear systems

${\begin{cases}y=mx+b_{1}\\y=-x/m\end{cases}}$

and

${\begin{cases}y=mx+b_{2}\\y=-x/m\end{cases}}$

to get the coordinates of the points. The solutions to the linear systems are the points

$\left(x_{1},y_{1}\right)\ =\left({\frac {-b_{1}m}{m^{2}+1}},{\frac {b_{1}}{m^{2}+1}}\right)\,$

and

$\left(x_{2},y_{2}\right)\ =\left({\frac {-b_{2}m}{m^{2}+1}},{\frac {b_{2}}{m^{2}+1}}\right).$

These formulas still give the correct point coordinates even if the parallel lines are horizontal (i.e., m = 0). The distance between the points is

$d={\sqrt {\left({\frac {b_{1}m-b_{2}m}{m^{2}+1}}\right)^{2}+\left({\frac {b_{2}-b_{1}}{m^{2}+1}}\right)^{2}}}\,,$

which reduces to

$d={\frac {|b_{2}-b_{1}|}{\sqrt {m^{2}+1}}}\,.$

When the lines are given by the general form of the equation of a line (horizontal and vertical lines are included):

$ax+by+c_{1}=0\,$

$ax+by+c_{2}=0,\,$

their distance can be expressed as

$d={\frac {|c_{2}-c_{1}|}{\sqrt {a^{2}+b^{2}}}}.$

 Two lines in three-dimensional space

Two lines in the same three-dimensional space that do not intersect need not be parallel. Only if they are in a common plane are they called parallel; otherwise they are called skew lines.

Two distinct lines l and m in three-dimensional space are parallel if and only if the distance from a point P on line m to the nearest point on line l is independent of the location of P on line m. This never holds for skew lines.

 A line and a plane

A line m and a plane q in three-dimensional space, the line not lying in that plane, are parallel if and only if they do not intersect.

Equivalently, they are parallel if and only if the distance from a point P on line m to the nearest point in plane q is independent of the location of P on line m.

 Two planes

Similar to the fact that parallel lines must be located in the same plane, parallel planes must be situated in the same three-dimensional space and contain no point in common.

Two distinct planes q and r are parallel if and only if the distance from a point P in plane q to the nearest point in plane r is independent of the location of P in plane q. This will never hold if the two planes are not in the same three-dimensional space.

 امتداد إلى الهندسة غير الإقليدية

In non-Euclidean geometry, it is more common to talk about geodesics than (straight) lines. A geodesic is the shortest path between two points in a given geometry. In physics this may be interpreted as the path that a particle follows if no force is applied to it. In non-Euclidean geometry (elliptic or hyperbolic geometry) the three Euclidean properties mentioned above are not equivalent and only the second one,(Line m is in the same plane as line l but does not intersect l ) since it involves no measurements is useful in non-Euclidean geometries. In general geometry the three properties above give three different types of curves, equidistant curves, parallel geodesics and geodesics sharing a common perpendicular, respectively.

 الهندسة الزائدية

انظر أيضاً: الهندسة الزائدية

الخطوط المتقاطعة والمتوازية و فائقة التوازي عبر a بالنسبة إلى l في المستوى الزائدي. الخطوط المتوازية تبدو متقاطعة في l مباشرة خارج الصورة. وهذا هو مجرد an artifact of the visualisation. On a real hyperbolic plane the lines will get closer to each other and 'meet' in infinity.

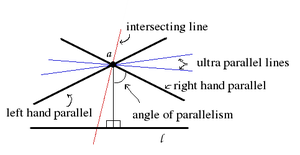
While in Euclidean geometry two geodesics can either intersect or be parallel, in hyperbolic geometry, there are three possibilities. Two geodesics belonging to the same plane can either be:

1. intersecting, if they intersect in a common point in the plane,
2. parallel, if they do not intersect in the plane, but converge to a common limit point at infinity (ideal point), or
3. ultra parallel, if they do not have a common limit point at infinity.

In the literature ultra parallel geodesics are often called non-intersecting. Geodesics intersecting at infinity are called limiting parallel.

As in the illustration through a point a not on line l there are two limiting parallel lines, one for each direction ideal point of line l. They separate the lines intersecting line l and those that are ultra parallel to line l.

Ultra parallel lines have single common perpendicular (ultraparallel theorem), and diverge on both sides of this common perpendicular.

 الهندسة الكرية أو الناقصية

انظر أيضاً: الهندسة الكرية and الهندسة الناقصية

على الكرة لا يوجد شيء مثل خط موازي. Line a is a great circle, the equivalent of a straight line in spherical geometry. Line c is equidistant to line a but is not a great circle. It is a parallel of latitude. Line b is another geodesic which intersects a in two antipodal points. They share two common perpendiculars (one shown in blue).

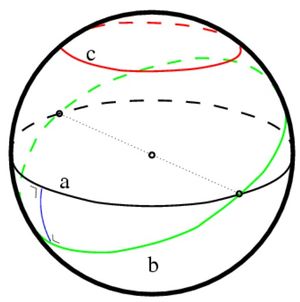
In spherical geometry, all geodesics are great circles. Great circles divide the sphere in two equal hemispheres and all great circles intersect each other. Thus, there are no parallel geodesics to a given geodesic, as all geodesics intersect. Equidistant curves on the sphere are called parallels of latitude analogous to the latitude lines on a globe. Parallels of latitude can be generated by the intersection of the sphere with a plane parallel to a plane through the center of the sphere.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 انظر أيضاً

• Clifford parallel
• Limiting parallel
• منحنى موازي
• Ultraparallel theorem

 المراجع

• Heath, Thomas L. (1956), The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.), New York: Dover Publications 

(3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3). Heath's authoritative translation plus extensive historical research and detailed commentary throughout the text.

• Richards, Joan L. (1988), Mathematical Visions: The Pursuit of Geometry in Victorian England, Boston: Academic Press, ISBN 0-12-587445-6 
• Wilson, James Maurice (1868), Elementary Geometry (1st ed.), London: Macmillan and Co. 
• Wylie Jr., C. R. (1964), Foundations of Geometry, McGraw–Hill 

 للاستزادة

• Papadopoulos, Athanase; Théret, Guillaume (2014), La théorie des parallèles de Johann Heinrich Lambert : Présentation, traduction et commentaires, Paris: Collection Sciences dans l'histoire, Librairie Albert Blanchard, ISBN 978-2-85367-266-5 

 وصلات خارجية

• Constructing a parallel line through a given point with compass and straightedge