دالة رتيبة

رسم 1: دالة رتيبة تصاعدية (في بعض أجزائها، فإنّ الدالة مجرد دالة رتيبة غير تنازلية، وفي باقي الأجزاء فالدالة تصاعدية تمامًا).

رسم 2: دالة رتيبة تنازلية.

رسم 3: دالة غير رتيبة.

الدالة الرتيبة في الرياضيات هي دالة تحافظ على ترتيب ما. نشأ مصطلح الدالة الرتيبة من حساب التفاضل والتكامل وعمّم لاحقًا لما يطلق عليه أسم نظرية الترتيب.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

الدوال الرتيبة في التحليل الرياضي وحساب التفاضل والتكامل

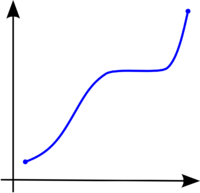
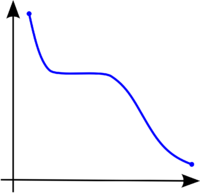
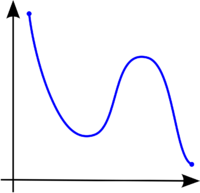
في سياق التحليل الرياضي وحساب التفاضل والتكامل، تدعى الدالة الحقيقيّة f المعرفة على مجموعة جزئية من الأعداد الحقيقية دالة رتيبة تصاعدية (أحيانًا، دالة تصاعدية أو غير تنازليّة)، إذا كان لكل x ≤ y يتحقّق أيضًا $f(x)\leq f(y)$ ، أي أنّها تحافظ على الترتيب (أنظر رسم 1). وبحسب نفس المنطق، فإنّ f رتيبة تنازلية (تنازلية أو غير تصاعدية) إذا كان لكل x ≤ y يتحقّق أيضًا $f(x)\geq f(y)$ ، أي أنّ الدالة تعكس الترتيب (انظر رسم 2).

إذا ما استبدلت اشارات "الأكبر أو يساوي" ≤ بإشارات "أكبر من" < نحصل على شرط أقوى. في هذه الحالة يطلق على الدوال اسم تصاعدية تمامًا أو تنازلية تمامًا بالتناظر. ومن خواص هذه الدوال أنّها دوال واحد لواحد (أي بالامكان تعريف دالة عكسية لها)، أذ أنّه إذا كان لـx ولـy قيمتين مختلفتين، فإمّا أن يكون x < y أو x > y، وحسب نوع الدالة الرتيبة (تصاعدية أم تنازلية تمامًا) يكون $f(x)<f\left(y\right)$ أو $f(x)>f\left(y\right)$ ، وعلى كل حال فإنّ $f(x)\neq f(y)$ وهو ما يجعلها دالة واحد لواحد.

الدوال البولية

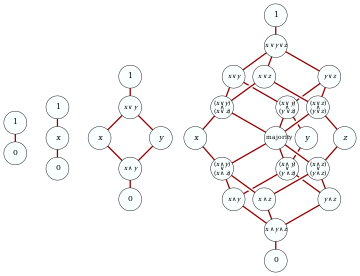
العناقيد التوزيعية الحرة للدوال البولية الرتيبة على المتغيرات 0, 1, 2, و 3 .

في الجبر البولي، الدالة الرتيبة هي تلك التي يكون فيها لكل a_i و b_i في {0,1} بحيث a₁ ≤ b₁, a₂ ≤ b₂, ... , a_n ≤ b_n

فإنه صحيح أن:

f(a₁, ... , a_n) ≤ f(b₁, ... , b_n).

الدوال البولية الرتيبة هم بالدقة اولئك اللائي يمكن تعريفهن كتركيب ل ands (conjunction) و ors (disjunction)، ولكن بدون nots (نفي).

عدد تلك الدوال على n متغير يـُعرف بإسم عدد ددكيند Dedekind number لـ n.

بعض الخواص والنتائج الأساسية

الخواص التالية صحيحة لأي دالة رتيبة $f:\mathbb {R} \to \mathbb {R}$ :

للدالة f نهاية من اليمين ومن اليسار في كل نقطة من نطاق الدالة؛
للدالة f نهاية في اللانهاية (في $\infty$ و $-\infty$ )، وقد تكون تلك إمّا عددًا حقيقيًا أو $\infty$ أو $-\infty$ ؛
أيّة نقاط نقاط عدم استمرار للدالة f تكون حتمًا من نوع قفزة؛