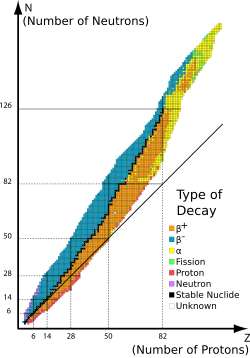اضمحلال بيتا

اضمحلال β− في نواة ذرة. الانبعاث الأوسط لبوزون W− افتراضي محذوف.

فيزياء نووية المواضيع الرئيسية انحلال مشع انشطار نووي اندماج نووي انحلالات تقليدية انحلال ألفا · انحلال بيتا · إشعاع گاما · Cluster decay انحلالات متقدمة انحلال بيتا مزدوج · Double electron capture · Internal conversion · Isomeric transition عمليات الانبعاث Neutron emission · Positron emission · Proton emission Capturing Electron capture · Neutron capture R · S · P · Rp الانشطار Spontaneous fission · Spallation · Cosmic ray spallation · Photodisintegration تخليق نووي Stellar Nucleosynthesis Big Bang nucleosynthesis Supernova nucleosynthesis العلماء هنري بكرل · بثه · ماري كوري · پيير كوري · إنريكو فرمي · غيرهم

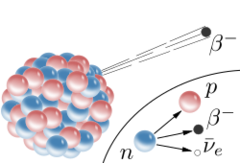
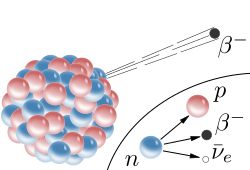
اضمحلال بيتا أو تحلل بيتا (Beta decay) (أو البِلَىً البِيتائِيّ) هو ظاهرة نشاط إشعاعي لعناصر كثيرة، تطلق فيه تلك العناصر أشعة بيتا. ثم اكتشف العلماء أن أشعة بيتا هذه ماهي إلا إلكترونات تنطلق من الذرة، ولما كان العنصر المصدر لتلك الإلكترونات يتحول أثناء تلك العملية التلقائية إلى عنصر آخر يتلوه مباشرة في الجدول الدوري توصلوا إلى حقيقة مصدر تلك الجسيمات فهي تصدر من أنوية تلك العناصر المشعة. وبزيادة الأبحاث إتضح انه يوجد نوعان لهذا التحلل : النوع الأول يحدث لبعض العناصر الغير مستقرة (ذات النشاط الإشعاعي) وتُصدر إلكترونات، والنوع الثاني فهي عناصر تطلق إلكترونات ذات شحنة كهربائية موجبة فأسموه بوزيترون. (وكلمة بوزيترون تأتي من كلمتي positive electron.) في كلتا الحالتين يتحلل العنصر المـُصدر لتلك الجسيمات إما إلى عنصر آخر يتلوه مباشرة في الجدول الدوري في حالة إصداره إلكترونا، أو يتحلل إلى عنصر قبله مباشرة في الجدول الدوري إذا أشع أو أطلق بوزيترونا. والبوزيترون يتساوى مع الإلكترون في كتلته وفي عزمه المغزلي (أي عزم دورانه حول محوره مثل المغزل)، ويتساوي معه أيضا في مقدار شحنته الكهربائية ،والاختلاف بينهما يكاد ينحصر في كون الإلكترون سالب الشحنة والبوزيترون موجب الشحنة. والبوزيترون هو نقيض الإلكترون وهناك من يسميه (مضاد الإلكترون).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 اضمحلال β−

في هذا التحلل لأحد العناصر يتحلل أحد نيوترونات النواة بواسطة التآثر الضعيف الذي يدخل فيه بوزون من نوع W− كعامل مساعد، يتحلل النيوترون إلى بروتون وإلكترون.

${}_{0}^{1}\mathrm {n} \to {}_{1}^{1}\mathrm {p} +\mathrm {e} ^{-}+{\overline {\nu }}_{e}$ .

وطبقا لقانون انحفاظ الشحنة الكهربائية نجد أن البروتون الناتج عن التحلل شحنته موجبة وهي تساوي تماما شحنة الإلكترون الناتج أيضا عن التحلل وبذلك تتعادل مجموع الشحنتين اللتين علي اليمين من المعادلة، والى اليسار من المعادلة نجد النيوترون وهو متعادل الشحنة الكهربية. بذلك يتحقق قانون احتفاظ الشحنة الكهربية. وكما على يمين المعادلة نجد انطلاق نقيض نيوترينو إلكتروني، وهو جسيم كتلته تقترب من الصفر، ولكنه أحد الأطراف الناتجة عن التحلل ويشارك البروتون والإلكترون في حمل الطاقة الناتجة عن التحلل والانطلاق بها خارج النواة وخارج الذرة. ويجدر هنا الإشارة إلى أن نوع التيوترينو المطلق من هذه العملية اسمه نقيض نيوترينو-الإلكترون، بسبب وجود ستة أنواع من النيوترينو، نكتفي هنا بذكر الجسيم المسمى نقيض نيوترينو الإلكترون، كما يسميه البعض (مضاد نيوترينو- الإلكترون).

شكل طبقا لاقتراح فينمان لتوضيح تحلل النيوترون إلى بروتون مع إطلاق نقيض نيوترينو-الإلكترون، في وجود البوزيترون W− كعامل مساعد.

صورة لظاهرة تحلل البيتا حيث يتحلل أحد نيوترونات النواة متحولا إلى بروتون ومطلقاً إلكترون ونيوترينو

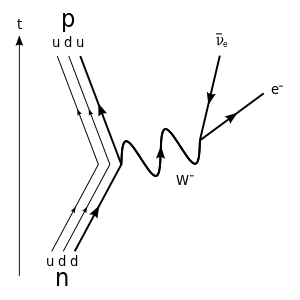
• لا يزال عالم الذرة والجسيمات الأولية يحمل كثيرا من علامات الاستفهام، وطبقا لنظرية جديدة بدأت تأخذ مكانتها بين العلماء منذ 1980، نوضح تحلل التحلل بإصدار إلكترونا كما في الشكل. تقول النظرية الجديدة أن النيوترون مكون من ثلاثة جسيمات صغيرة اسمها كواركات وهم من نوع u,d,d. وأن البروتون هو الآخر مكون من ثلاثة أنواع أخرى من الكواركات، وهم كما في الشكل u,d,u. وأن ما يحدث خلال التحلل هو تحلل أحد كواركات النيوترون من نوع d إلي كوارك من نوع u مع إطلاق إلكترونا ونقيض نيوترينو-الإلكترون، فيصبح بروتونا. وهذا ما يوضحه الشكل على اليسار حيث تسير عملية التحلل من أسفل إلى أعلى.

• في الواقع يتحلل النيوترون الحر، أي الطليق غير محبوس داخل نواة ذرة، يتحلل خلال 15 دقيقة على النحو الموصوف أعلاه. ونفس هذه العملية يتبعها النيوترون عندما يتحلل وهو حبيس داخل نواة الذرة. وكل ما في الأمر أنه داخل النواة يستطيع التمتع بحياة أطول عنه من أن يكون حرا طليقا. ففي النواة يستطيع النيوترون العيش لمدة ملايين السنين أو أحيانا لمدة ثوان فقط، كل ذلك يعتمد على نوع العنصر الداخل في تكوينه.

• وكما توجد عناصر تتحلل بطرد الإلكترونات (جسيمات بيتا) توجد عناصر تتحلل بطرد البوزيترونات (جسيمات بيتا الموجبة الشحنة)، ونوضح ذلك في الآتي:

 اضمحلال β+

انظر أيضاً: انبعاث الپوزيترون

سنستعمل شكل فاينمان الذي شرح لنا كيفية تحلل النيوترون إلي بروتون وإلكترون ونقيض نيوترينو-الإلكترون بوساطة أحد الجسيمات الثقيلة المسماة W−. في حالة التحلل بإصدار بوزيترونا (e+) لا بد من تواجد فائض من الطاقة في نواة الذرة تكفي لتكوين البوزيترون (وكتلته مثل الإلكترون = 0,511 MeV). (وهذا مثال لتحول الطاقة إلى كتلة لها وزن بحسب علاقة أينشتين التي تعطينا العلاقة بين الكتلة والطاقة E=m.c**2، انظر تفاعل نووي). ويتم هذا التحلل بوساطة توزون ثقيل مع إطلاق نيوترينو-إلكترون :

energy + p+ → n0 + e+ + νe

ويلاحظ هنا أن التحلل بإطلاق البوزيترون ليس كالتحلل بإطلاق الإلكترون، لأن البروتون أخف من النيوترون ولابد من تواجد طاقة كافية لتوليد البوزيترون، وهذه الطاقة تـُستمد من نواة الذرية. وبدونها لا يمكن تحول البروتون إلى نيوترون. تلك الطاقة الزائدة المحتجزة في النواة تعنل على تحول البروتون إلى نيوترون وتوليد البوزيترون ونيوترينو-الإلكترون وإعطائهم طاقة الحركة التي ينطلقان بها خارج الذرة.

 Nuclear transmutation

If the proton and neutron are part of an atomic nucleus, these decay processes transmute one chemical element into another. For example:

137 55Cs			→	137 56Ba	+	e−	+	νe	(beta minus decay)
22 11Na			→	22 10Ne	+	e+	+	νe	(beta plus decay)
2211Na	+	e−	→	22 10Ne	+	νe			(electron capture)

 الانتقالات الممنوعة

Beta decays can be classified according to the L-value of the emitted radiation. When L > 0, the decay is referred to as "forbidden." Nuclear selection rules require high L-values to be accompanied by changes in nuclear spin (J) and parity (π). The selection rules for the L^th forbidden transitions are:

$\Delta J=L-1,L,L+1;\Delta \pi =(-1)^{L},$

where Δπ = 1 or -1 corresponds to no parity change or parity change, respectively. The special case of a 0⁺ → 0⁺ transition is referred to as "superallowed". The following table lists the ΔJ and Δπ values for the first few values of L:

Forbiddenness	ΔJ	Δπ
Superallowed	0+ → 0+	no
Allowed	0, 1	no
First forbidden	0, 1, 2	yes
Second forbidden	1, 2, 3	no
Third forbidden	2, 3, 4	yes

 طيف انبعاث بيتا

Beta decay can be considered as a perturbation as described in quantum mechanics, and thus Fermi's Golden Rule can be applied. This leads to an expression for the kinetic energy spectrum N(T) of emitted betas as follows:

$N(T)=C_{L}(T)F(Z,T)pE(Q-T)^{2}$

where T is the kinetic energy, C_L(T) is a shape function that depends on the forbiddenness of the decay (it is constant for allowed decays), F(Z,T) is the Fermi Function (see below) with Z the charge of the final-state nucleus, E = T + m c² is the total energy, p = [(E/c)² - (mc)²]^1/2 is the momentum, and Q is the Q value of the decay. The kinetic energy of the emitted neutrino is given approximately by Q minus the kinetic energy of the beta.

 دالة فرمي

$F(Z,T)={\frac {2(1+S)}{\Gamma (1+2S)^{2}}}(2p\rho )^{2S-2}e^{\pi \eta }|\Gamma (S+i\eta )|^{2},$

where S = [1 - α² Z²]^1/2 (α is the fine-structure constant), η = ± α Z E / p (+ for electrons, - for positrons), ρ = r_N / ℏ (r_N is the radius of the final state nucleus), and Γ is the Gamma function.

For non-relativistic betas (Q << m_ec²), this expression can be approximated by:

$F(Z,T)\approx {\frac {2\pi \eta }{1-e^{-2\pi \eta }}}.$

 التقاط K

K في البناء الذري هو الغلاف الأول والأقرب إلى النواة، ويدور فيه اثنان من إلإلكترونات، ويحدث أحيانا أن تلتقط النواة ذات الشحنة الموجبة أحد تلك الإلكترونات التي تدور حولها بفعل القوة الإلكتروستاتيكية. فيتعادل هذا الإلكترون مع أحد البروتونات في النواة مكونا نيوترونا. وبذلك ينخفض عدد البروتونات الموجودة في النواة بمقدار بروتون واحد، ويزيد عدد النيوترونات بنيوترون واحد ،ويتحول العنصر إلى عنصر آخر قبله طبقا للترتيب الدوري للعناصر، ويحتفظ مع ذلك بوزنه الذري. حينما ينهار أحد إلكترونات الغلاف Kعلى النواة يصبح مكانه فارغا وتصبح الذرة في حالة إثارة. ويمكنها النزول إلى الحالة الأرضية المستقرة عن طريق أن يقفز أحد إلكترونات الغلاف الخارجي للذرة ليشغل الفراغ في الغلاف K وتستقر الذرة مع إصدارها لطاقة ربط الإلكترون القافز من الغلاف الخارجي لملء الغلاف K. وتطهر تلك الطاقة على هيئة شعاع كهرطيسي من الأشعة السينية، تكون طاقته عادة عشرات eV وهذه أضعف كثيرا عن أشعة جاما التي تنتج أثناء التحلل بيتا، والتي تنتجها النواة. هذا هو التقاط إلكترون K، كما يمكن أن يحدث أن تلتقط النواة إلكترونا من الغلاف L، فتسمى عملية تحول العنصر إلى عنصر آخر في هذا الحالة التقاط L.

صورة لظاهرة تحلل البيتا

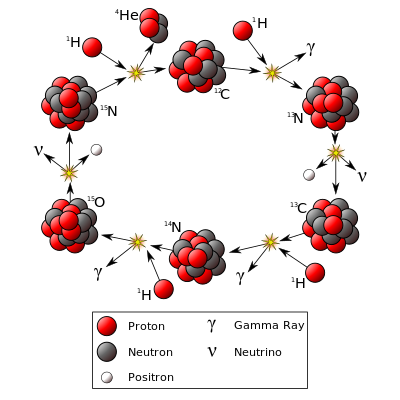
 دورة الكربون والنيتروجين والأكسجين (CNO)

هذه دورة من الدورات التي تحدث في الشمس والتي تتولد خلالها عناصر مختلفة أثقل من الهيدروجين، ويحدث ذلك بمساعدة تحلل البيتا. من ناحية المبدأ يمكن تنفيذ تلك الدورة في معمل الفيزياء. وهي تتضمن تحول الكربون إلى النيتروجين إلى الأكسجين ثم إلى الكربون ثانيا في دورة مستمرة، وتحتوي علي عمليتين للتحلل بيتا نريد توضيحهما هنا وهما علي يمين الشكل وعلى يساره :

نبدأ الدورة من أعلى حيث يتحول الكربون-12 (C-12) بسبب اصطدامه بأحد البروتونات H-1 ويتحد معه مـُصدرا شعاع جاما ويصبح ذرة نيتروجين N-13. يتحول هذا النيتروجين-13 إلى الكربون-13 بإطلاق بوزيترون ونيوترنو (وهذا هو التحلل بيتا الأول في هذه الدورة). ثم يدخل الكربون-13 في تفاعل نووي مع أحد البروتونات H-1 (على يمين الشكل) ويتحول إلى نيتروجين-14 مع إطلاق شعاع جاما. ويصطدم النيتروجين-14 ببروتون H-1 ويتفاعل معه ويصبح أكسجين-15 ويطلق شعاع جاما. علي شمال الشكل نجد تحلل بيتا الثاني حيث يتحلل أحد البروتونات في الأكسجين-15 (O-15) إلى نيتروجين-15 ويطلق بوزيترونا ونيوترنو، ثم يدخل النيتروجين-15 في تفاعل مع بروتون أخرا H-1 وينتج عن التفاعل نواة الهيليوم He-4 وكربون-13.

ويحدث في الشمس العديد مثل تلك الدورة مع عناصر أخرى، فالشمس ما هي إلا مفاعل نووي كبير، يندمج فيه الهيدروجين إلى هيليوم ثم إلى عناصر ثقيلة. والشمس ماهي إلا مطبخ للعناصر والوقود فيها هو الهيدروجين.

 انظر أيضا

• تحلل أسي
• نفق ميكانيكا الكم
• دورة CNO
• جسيم بيتا
• اصطياد إلكترون
• تحلل ألفا
• تفاعل نووي
• جدول النظائر
• نافذة جاموف

 الهامش

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 وصلات خارجية

• The Live Chart of Nuclides - IAEA with filter on decay type