هندسة تحليلية

الأحداثيات الديكارتية.

الهندسة التحليلية وتدعى أيضا الهندسة الأحداثية أو التنسيقية وسابقا الهندسة الديكارتية, هي فرع المعرفة الرياضية الذي تم من خلاله الربط بين فرعي الهندسة والجبر.

وتهتم الهندسة التحليلية بالمواضيع ذاتها التي تهتم بها الهندسة التقليدية غير أنها تتيح طرقا أيسر لبرهان العديد من النظريات وتلعب دورا مهما في حساب المثلثات وحساب التفاضل والتكامل، وتهتم أيضا بدراسة الخواص الهندسية للأشكال باستخدام الوسائل الجبرية عادة تستخدم جمل إحداثيات ديكارتية لوصف نقاط الفراغ بدلالة أرقام هي الإحداثيات ثم يتم إيجاد المعادلة الجبرية التي تصف كلا من الدائرة أو القطع الناقص أو القطع المكافيء.

تقوم الهندسة التحليلية على وصف الأشكال الهندسية بطريقة جبرية عددية، واستخراج معلومات رقمية من تمثيلات هندسية.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 مثال

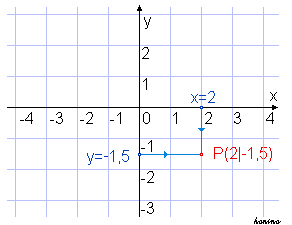
الشكل الجبري للدائرة هي : (x^2-2)+(y^2-2)=0) حيث نصف قطر الدائرة هنا هو (2) وبشكل عام : (س^2-أ)+(ع^2-أ)=0 و نصف قطر الدائرة هنا هو (أ)

 الأحداثيات

المقالة الرئيسية: نظام الأحداثيات

تستخدم الهندسة التحليلية نطاقا إحداثيا يسمى النظام الديكارتي نسبة إلى العالم الفرنسي رينيه ديكارت (1596 – 1650 ) صاحب الفكرة الأساسية للربط بين الهندسة والجبر وهي تمثيل كل نقطة في المستوي ببعديها عن مستقيمين متعامدين يلتقيان في نقطة تسمى نقطة الأصل ( 0 ، 0 ). يسمي المستقيمان المتعامدان محوري الإحداثيات 0 المحور الأفقي هو المحور السيني والمحور الراسي هو المحو الصادي ويحدد موقع النقاط في المستوي بإعطائها إحداثيين على خطى الأعداد.

س ، ص ويسمي س الاحداثي السيني وهو يحدد موقع النقطة بالنسبة لمحور السينات بينما يحدد ص الاحداثي الصادي موقع النقطة بالنسبة لمحور الصادات ويكتب هذان الإحداثيان على صورة زوج مرتب (س ، ص ) .

- ترتبط كل نقطة في المستوي بزوج مرتب وحيد من الأعداد (س ، ص )وأيضا كل زوج مرتب يرتبط بنقطة واحدة وواحدة فقط في المستوي.

محوري الإحداثيات يقسمان المستوي الإحداثي إلى أربعة أرباع:

• الربع الأول = ة ( س، ص) : س < 0 ، ص < 0 : س ، ص ي ح’
• الربع الثاني = ة ( س ، ص ) : س > 0 ، ص . , ص > 0 : س ، ص ي ح’
• الربع الرابع = ة ( س ، ص : س < 0 ، ص > 0 : س ، ص ي ح’

كذلك يمكن وصف المحور السيني والمحور الصادي كمجموعة من النقاط كالتالي :-

• المحور السيني = ة( س،ص) : س ي ح ، ص = 0 ’
• المحور الصادي = ة (س،ص) : ص ح ، س= 0 ’

 بعض القوانين في الهندسة التحيلية

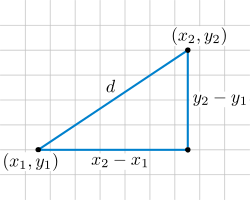
 المسافة بين نقطتين في مستوي الإحدثيات

لتكن أ ب قطعة مستقيمة أ ( س1،ص1 ) ، ب ( س2 ، ص2 ) فان المسافة بين النقطتين ا ، ب هي

$AB^{2}=(X1-X2)^{2}+(Y1-Y2)^{2}$

 إحداثيا نقطة المنتصف للقطعة المستقيمة أ ب هي

$[(x1+x2)/2,(y1+y2)/2]$

 ميل الخط المستقيم

""تعرف"":هي الزاوية المحصورة بين محور السينات الموجب و المتستقيم

الميل يساوي فرق الصادات على فرق السينات

م= (ص2-ص1)/(س2-س1):حيث أن س1 لا تساوي س2

ملاحظة : المستقيم الذي يوازي محور الصادات ليس له ميل و المستقيم الذي يوازي محور السينات ميله يساوي صفر

و الميل يساوي ظل الزاوية المحصورة بين محور السينات الموجب و المستقيم

م= ظاه

 معادلات المنحنيات

In analytic geometry, any equation involving the coordinates specifies a subset of the plane, namely the solution set for the equation. For example, the equation y = x corresponds to the set of all the points on the plane whose x-coordinate and y-coordinate are equal. These points form a line, and y = x is said to be the equation for this line. In general, linear equations involving x and y specify lines, quadratic equations specify conic sections, and more complicated equations describe more complicated figures.

Usually, a single equation corresponds to a curve on the plane. This is not always the case: the trivial equation x = x specifies the entire plane, and the equation x² + y² = 0 specifies only the single point (0, 0). In three dimensions, a single equation usually gives a surface, and a curve must be specified as the intersection of two surfaces (see below), or as a system of parametric equations. The equation x² + y² = r² is the equation for any circle with a radius of r.

The distance formula on the plane follows from the Pythagorean theorem.

 المسافة والزاوية

In analytic geometry, geometric notions such as distance and angle measure are defined using formulas. These definitions are designed to be consistent with the underlying Euclidean geometry. For example, using Cartesian coordinates on the plane, the distance between two points (x₁, y₁) and (x₂, y₂) is defined by the formula

$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}},\!$

which can be viewed as a version of the Pythagorean theorem. Similarly, the angle that a line makes with the horizontal can be defined by the formula

$\theta =\tan ^{-1}(m)\!$

where m is the slope of the line.

 التحولات

Transformations are applied to parent functions to turn it into a new function with similar characteristics. For example, the parent function y=1/x has a horizontal and a vertical asymptote, and occupies the first and third quadrant, and all of its transformed forms have one horizontal and vertical asymptote,and occupies either the 1st and 3rd or 2nd and 4th quadrant. In general, if y = f(x), then it can be transformed into y = af(b(x − k)) + h. In the new transformed function, a is the factor that vertically stretches the function if it is greater than 1 or vertically compresses the function if it is less than 1, and for negative a values, the function is reflected in the x-axis. The b value compresses the graph of the function horizontally if greater than 1 and stretches the function horizontally if less than 1, and like a, reflects the function in the y-axis when it is negative. The k and h values introduce translations, h, vertical, and k horizontal. Positive h and k values mean the function is translated to the positive end of its axis and negative meaning translation towards the negative end.

 الموضوعات

Important themes of analytical geometry are

• vector space
• definition of the plane
• distance problems
• the dot product, to get the angle of two vectors
• the cross product, to get a perpendicular vector of two known vectors (and also their spatial volume)
• intersection problems

Many of these problems involve linear algebra.

 مثال

Here an example of a problem from the United States of America Mathematical Talent Search that can be solved via analytic geometry:

Problem: In a convex pentagon $ABCDE$, the sides have lengths $1$, $2$, $3$, $4$, and $5$, though not necessarily in that order. Let $F$, $G$, $H$, and $I$ be the midpoints of the sides $AB$, $BC$, $CD$, and $DE$, respectively. Let $X$ be the midpoint of segment $FH$, and $Y$ be the midpoint of segment $GI$. The length of segment $XY$ is an integer. Find all possible values for the length of side $AE$.

Solution: Without loss of generality, let $A$, $B$, $C$, $D$, and $E$ be located at $A=(0,0)$, $B=(a,0)$, $C=(b,e)$, $D=(c,f)$, and $E=(d,g)$.

Using the midpoint formula, the points $F$, $G$, $H$, $I$, $X$, and $Y$ are located at

$F\left({\frac {a}{2}},0\right)$, $G\left({\frac {a+b}{2}},{\frac {e}{2}}\right)$, $H\left({\frac {b+c}{2}},{\frac {e+f}{2}}\right)$, $I\left({\frac {c+d}{2}},{\frac {f+g}{2}}\right)$, $X\left({\frac {a+b+c}{4}},{\frac {e+f}{4}}\right)$, and $Y\left({\frac {a+b+c+d}{4}},{\frac {e+f+g}{4}}\right).$

Using the distance formula,

$AE={\sqrt {d^{2}+g^{2}}}$

and

$XY={\sqrt {{\frac {d^{2}}{16}}+{\frac {g^{2}}{16}}}}={\frac {\sqrt {d^{2}+g^{2}}}{4}}.$

Since $XY$ has to be an integer,

$AE\equiv 0{\pmod {4}}$

(see modular arithmetic) so $AE=4$.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الهندسة التحليلية الحديثة

المقالة الرئيسية: هندسة جبرية

للمزيد من المعلومات: هندسة مركبة

An analytic variety is defined locally as the set of common solutions of several equations involving analytic functions. It is analogous to the included concept of real or complex algebraic variety. Any complex manifold is an analytic variety. Since analytic varieties may have singular points, not all analytic varieties are manifolds.

Analytic geometry is essentially equivalent to real and complex Algebraic geometry as it has been shown by Jean-Pierre Serre in his paper GAGA, whose name is, in French, Algebraic geometry and analytic geometric. Nevertheless, the two fields remain distinct, as the methods of proof are quite different and algebraic geometry includes also geometry in finite characteristic.

 وصلات خارجية

• Coordinate Geometry topics with interactive animations
• Build analytic geometry objects