انصعاق
ينشأ الانصعاق أو التفرقع detonation عن انفجار غير متجانس heterogenous لمادة متفجرة ينشر موجة صدم تنطلق في الوسط الذي يوجد فيه فيتسبب في إحداث تغيير في حجمه وضغطه ودرجة حرارته وسرعته المادية، ويتم كل ذلك بسرعة تدعى «سرعة الانصعاق»، تراوح بين 2000م/ثا و9000م/ثا. ويستفاد من ظاهرة الانصعاق خصوصاً في القلع والتقويض والتخريب وإحداث الانفجار.[1]
لمحة تاريخية
عُرف الانصعاق بادئ ذي بدء على أنه انفجار ينتشر بمنتهى السرعة عند استعمال مُشْعِلٍ (كبسولة) مناسب، ويمكن أن يؤدي بسبب سرعته إلى أفعال تدمير وتحطيم وتهديم تختلف كثيراً عما يؤدي إليه اضطرام deflagration المتفجرات العادية. وقد قيست سرعة انصعاق المتفجرات بساعات التوقيت المستعملة في قياس سرعة القذائف. وبالاعتماد على هذه القياسات وَجَدَ فريدرك أوگست آبل F.A.Abel عام 1874 أن البارود القطني ينصعق بسرعة تراوح بين 5300م/ثا و 6800م/ثا، وأن هذه السرعة تزداد بازدياد كثافة المتفجر بفعل الضغط. وتبين أن البارود القطني المحدّد الكثافة، الذي يحتوي على 15% من الماء يَنْصعق بسرعة أكبر من سرعة انصعاق المتفجر الجاف نفسه. وبدا ذلك غريباً وظاهري التناقض، إلا أن النظرية فسرته فيما بعد. وابتكر هنريخ دوتريش H.Dautriche طريقة بارعة عام 1906 جعلت قياس سرعة الانصعاق أسهل إنجازاً. أما اليوم فإن الحواسيب الحديثة مكَّنت من قياس سرعة الانصعاق بدقة تبلغ 99.98%. ومع ذلك فإن دراسة المتفجرات الغازية هي التي أدت إلى معرفة صفات الانصعاق ووضع نظريته بعد أن اكتشف مارسلان برتلو M.Berthelot وپول ڤييّ P.Vielle من جهة، وإرنست مالار E.Mallard وهنري لوشاتلييه H.Lechatelier من جهة أخرى - كل فريق على حدة - الانصعاق في الغازات عام 1881.
الانصعاق في الغازات
ما إن يشعل مزيج غازي متفجر موضوع في أنبوب مغلق من إحدى نهايتيه حتى تبدأ سرعة اللهب بالازدياد تدريجياً وتصل في غالب الأحيان إلى درجة عالية جداً تبقى بعدها ثابتة تماماً من الناحية العملية، وقد تحقق برتلو وفيي من أن لكل مزيج غازي سرعة عظمى خاصة به. وأطلقا على هذا الأسلوب في انتشار اللهب بسرعة مرتفعة جداً اسم «موجة التفجر» وهي تعرف اليوم بالانصعاق، وتحققا أيضاً من أن هذه السرعة مستقلة عن المادة وعن قطر الأنبوب شريطة ألا يكون هذا القطر صغيراً بإفراط، وألا تتغير هذه السرعة عندما يعقب الانصعاق اضطرابات، وعندما يتم الإشعال دفعة واحدة بِفُلْمينات الزئبق fulminate de mercure مثلاً.
ولا تتغير سرعة الانصعاق إلا قليلاً بتغير درجة الحرارة والضغط البدائي للغاز المنفجر، ففي مزيج الهدروجين والأكسجين مثلاً 2H2+O2 تكون سرعة الانصعاق في الضغط الجوي العادي 2821م/ثا بدرجة حر ارة 10ْس، وتكون 2790م/ثا في درجة حرارة 100ْس، وهي تبلغ 2720م/ثا في الدرجة 10ْس عندما يكون الضغط 0.5 بار، وتبلغ 2875م/ثا عندما يكون الضغط 2 بار (البار يساوي ضغطاً جوياً تقريباً).
وقد وازن برتلو وفييّ بين سرعة موجة التفجر أي سرعة الانصعاق والسرعة الوسطى لجزيئات الغازات المحترقة في درجة الحرارة المرتفعة التي أوصلها إليها الانصعاق فوجدا قيماً من الرتبة نفسها. واعتقد هارولد دكسون H.B.Dixon فيما بعد أن سرعة الانصعاق تساوي سرعة الصوت في الغازات المحترقة الساخنة. ودرس برنهارد ريمان B.Riemann، ثم هنري هوگونيو H.Hugoniot أمواج الصدم رياضياً. في حين توقع أرثر شوستر A.Schuster عام 1893 ثم ڤييّ عام 1897 وجود علاقة بين الانصعاق وانتشار أمواج الصدم. وفي عام 1899 وضع ديڤيد ليونار شاپمان D.L.Chapman معادلات عدَّ فيها الانصعاق موجة صدم ترافق تفاعلاً كيمياوياً، وهذا التفاعل هو في معظم الحالات تفاعل غاز قابل للاحتراق في الهواء أو الأكسجين أو أي غاز مُلْهِب آخر.
وإثر ذلك أطلق كروسار L.Crussard عام 1907 على هذه الظاهرة اسم «موجة الصدم والاحتراق». لأن سطح الموجة هو سطح انقطاع لا للسرعة المادية والضغط ودرجة الحرارة فقط ولكن يشمل أيضاً التركيب الكيمياوي.
وجاء إميل جوگيه E.Jouguet فوضع بين عامي 1901 و1906 النظرية الدقيقة لهذه الأمواج بمعزل عن شابمان، فَعُرفَت عالمياً باسم «شرط شاپمان - جوگيه» أو «النظرية الثرموديناميكية للانصعاق» لأن المعادلات الأساسية لهذه النظرية تصح على المتفجرات الغازية كما تصح على المتفجرات الصلبة، وإن كانت أصعب تطبيقاً على هذه الأخيرة لعدم معرفة معادلة حالة منتجات الانصعاق تحت ضغوط تراوح بين 50 و 300 كيلو بار.
الانصعاق في المتفجرات الصلبة والسائلة
يوافق انتشار الانصعاق في وسط متفجر انتشار موجة صدم، أي موجة يعاني منها حجم الوسط وضغطه ودرجة حرارته وسرعته على جانبيها تغيراً مباغتاً وعنيفاً. ويتوقف شكل موجة الصدم هذه على شكل المتفجر وطريقة إشعاله (إزكائه). ولما كانت دراسة انتشار هذه الأمواج من التعقيد بمكان فإن تناولها يتم هنا في حالة خاصة جداً.
الانصعاق المثالي
في هذه الحالة يمكن تخيل وسط منفجر لا حدود له مع افتراض عدم وجود الإشعال للتمكن من عد موجة الصدم موجة مستوية، وعد النظام نظاماً دائما. وعندئذ يوصف الانصعاق بكونه «مثالياً»، وتدعى موجة الصدم الموافقة باسم «موجة الانصعاق المثالي»، وهي تنتشر في الوسط المتفجر بسرعة تدعى «سرعة الانصعاق المثالي»، وهي تابعة لطبيعة المتفجر وكثافة حمولته.
إن سرعة الانصعاق المثالي هذه سرعة نظرية كلياً، إلا أن فائدتها تكمن في أن بالإمكان حسابها بسهولة ويسر باعتماد بعض الفرضيات المتممة من أجل إعطاء فكرة جيدة عن الواقع. وهي السرعة التي تتعمق عند انصعاق حشوة كبيرة القطر جداً شريطة أن يكون الانصعاق بعيداً جداً عن الإشعال (الإزكاء).
وتنحصر سرعة انصعاق المتفجر هذه عموماً بين 2000م/ثا (في حالة متفجر نتراتي يحتوي على 50 % من كلوريد الصوديوم)، و 9000 م/ثا (في حالة متفجر مضغوط يحتوي على 95 % من الأكتوجين (حلقي رباعي متيلن رباعي النترامين).
الانصعاق غير المثالي - مفهوم القطر الحرج
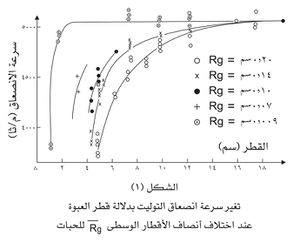
إن سرعة الانصعاق المثالي لمتفجر هي السرعة الناتجة عندما يكون قطر الحشوة كبيراً جداً. أما إذا وضعت المتفجرات الصلبة في عبوات أسطوانية مختلفة الأقطار وأُشعلت من أحد طرفيها. فقد وجد أن انصعاقها يعاني ضغطاً تحت قيمة محددة لقطر الصعقة، ثم يتوقف الانصعاق إذا أخذت هذه القيمة بالصغر، تاركاً جزءاً من المتفجر سليماً. ويتضح ذلك من رسم منحني تغير سرعة الانصعاق لشحنة متفجرة من البارود قيست بدقة بدلالة القطر. ويعطي هذا المنحني بالتمديد الخطي (الاستقراء) سرعة الانصعاق المثالي. ويبين الشكل التالي على سبيل المثال المنحنيات التجريبية الحاصلة عند انصعاق مادة التوليت tolite (ثلاثي نترات التولوين trinitrotoluene ت. ن. ت) وفق قياسات شتى لنسب الحبات.
ويطلق على هذا القطر الأصغري اسم «القطر الحرج» وهو يختلف باختلاف المتفجر كما يتضح من الجدول 1:
| المتفجر (في كثافة ارتصاص =1.10 غ/سم3 ) |
القطر الحرج للطلقة |
|---|---|
| صمغ الديناميت | 2 مم |
| التوليت (ت.ن.ت) | 12 مم |
| النتروستان | 18 مم |
وبزيادة القطر بدءاً من قيمته الحرجة تزداد سرعة الانصعاق حتى تبلغ قيمةً حدية ثابتة يوافقها ما يدعى «القطر الحدي». ويوصف الانصعاق عند استعمال الأقطار الأعلى قيمة من القطر الحدي باسم «الانصعاق المثالي». وفي الانصعاقات غير المثالية يفقد التمدد الجانبي لمنتجات الانصعاق جزءاً من الطاقة المغذِّية لموجة الصدم الخاصة المكوِّنة لجبهة الانصعاق، وتكون السرعة الملاحظة عندئذ أقل قيمة من سرعة الانصعاق المثالي. أما تحت القطر الحرج فيبلغ فَقْد الطاقة من الشدة حداً يستحيل معه حصول نظام انصعاق ثابت. أما في المتفجرات الموضوعة في عبوات (ظروف) معدنية ثخينة فإن هذه العبوات تعاكس التمدد الجانبي للغازات منْقِصة الفقْد في الطاقة ومتيحة الحصول على سرعة انصعاق مثالي بقطر أصغر من القطر الحدي.
| المتفجر | الكثافة | سرعة الانصعاق |
|---|---|---|
| نتروگليسرين | 1.60 گ/سم3 | 7600 م/ثا |
| نترو المتان | 1.145 گ/سم3 | 6630 م/ثا |
كما تتبع سرعة انصعاق المتفجرات الصلبة كثافةَ التحميل، ويكون هذا التابع خطياً عند انصعاق المتفجرات المنتْرجة العادية في مجال من الكثافات يراوح بين 1.10 غ/سم3 و1.60غ/سم3. وتنحصر سرعة انصعاق جميع هذه المتفجرات تقريباً بين 6500 م/ثا و 7500 م/ثا عندما تكون الكثافة مساوية 1.5 گ/سم3 وكذلك الحال في المتفجرات السائلة كما يتبين من الجدول 2:
ويكون القطر الحدي للمتفجرات الكلوراتية والنتراتية في الكثافات التي تستعمل فيها في أعمال اللَّغْم من الرتبة 100مم. وتتناقص سرعة انصعاق الحشوات ذات العبوات الورقية (وهي عبوات لاعطالة لها) وذوات الأقطار 25 مم أو 30 مم أو 40 مم، وهي الأكثر استعمالاً كلما ازداد صغر القطر. وتوافق كل قطر كثافة تكون فيها السرعة أعظمية وثابتة.
| المتفجر | ثخن منطقة التفاعل |
|---|---|
| الهكسوجين | 0.8 مم |
| حمض المر (البيكريك) | 2 مم |
| نتروگوانيدين | 9 مم |
وجاءت دراسة نقص السرعة بين القطر الحدي والقطر الحرج لتوضح ثخن منطقة التفاعل، أي المنطقة المحصورة بين جبهة موجة الصدم والمستوي المسمى «شرط شاپمان - جوگيه» حيث يتم التفاعل الكيمياوي غير القابل للانعكاس الناتج بالصدم، فوجِد ما يلي (الجدول 3):
ويتم تفاعل الانفجار في المنطقة المذكورة في مدة تراوح بين 0.1 ميكروثانية و1.2 ميكروثانية منصعقاً على جدار صلب رقيق على تماس مع المتفجر مؤدياً آنياً تقريباً إلى ضغط مرتفع قاذفاً بشظايا الجدار المذكور بسرعة تبلغ عدة كيلومترات في الثانية. ويمكن عند جعل هذه الشظايا تتجمع في نقطة الحصول على قدرة ثقب مرتفعة تبلغ فيها سرعة القذف 10 كم/ثا، وذلك إذا ما أُعطي الجدار شكلاً ملائماً (الحشوات الجوفاء).
ويمكن أن تُنتِج موجة الصدم الصادرة من متفجر ما في الهواء أفعالاً مدمِّرة مختلفة في الوسط المحيط، كما يمكن أن تصعق شحنةً متفجرة أخرى تقع على مسافة ما، ويطلق على هذه الظاهرة اسم «الانصعاق بالتأثير». تأثير الحصر: تنقص الخسارات الجانبية في الحالة التي تكون فيها طلقة المتفجر في داخل أنبوب، أي في مجال محصور، ويزداد هذا النقص بازدياد مقاومة الظرف الذي يحويها. ويستتبع هذا أن تكون سرعة انصعاق المتفجر تابعاً متزايداً لثخن الظرف عند ثبات القطر والمادة التي صنع منها الظرف. ويمكن من أجل كل حصر - عند ثبات ثخن الظرف ومادته - تحديد قطرٍ حرج يكون دائماً أدنى من القطر الحرج في حالة إبقاء الشحنة عارية.
وقد اقترح مُنظّرون كثيرون نماذج تتيح حساب سرعة الانصعاق في حالة الشحنات المحصورة. وأعطى جونز Jones النتيجة التالية: يجب في حالة متفجر (نتراتي مثلاً) طول منطقة التفاعل فيه س= 5مم والمشحون بكثافة قدرها 1.5 في أنبوب من حديد قطره الداخلي20مم، أن يكون ثخن المعدن مساوياً 24مم كي يكون النقص النسبي في سرعة الانصعاق «سر» بالنسبة إلى السرعة المثالية «سرم» مساوياً 1%. أي:
- ( سرم - سر ) / سر = 0.01
| من أجل س = 5 مم قط (مم) |
من أجل س = 2 مم قط (مم) |
(سرم - سر ) / سر | |
|---|---|---|---|
| 0.1 | 50 | 20 | 0.4% |
| 0.15 | 33.3 | 13.3 | 1.9% |
| 0.2 | 25 | 10 | 4.8% |
| 0.25 | 20 | 8 | 9.6% |
| 0.3 | 16.7 | 6.7 | 16.3% |
| 0.35 | 14.3 | 5.7 | 25.0% |
| 0.4 | 12.5 | 5 | 35.4% |
| 0.45 | 11.1 | 4.4 | 47.2% |
| 0.5 | 10 | 4 | 60.4% |
ويبين الجدول (4) أن هذا النقص النسبي في سرعة الانصعاق بالنسبة إلى السرعة المثالية يكافئ في حالة هذا النمط نفسه من المتفجر نقصاً يحصل بشحنة عارية قطرها قط= 40مم تقريباً.
الموضوعات ذات الصلة
- انفجار
- متفجر
- موجة الصدم
- قسم تفجير من متفجر، Detonator.
- اختبار نووي
- Detonation diamond
- Predetonation of nuclear weapons
- شرط شاپمان - جوگيه
- Engine knocking
المصادر
- ^ صلاح يحياوي. "الانصعاق". الموسوعة العربية. Retrieved 2009-06-22.