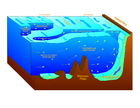
بروز مدي

Figure 1: Comet Shoemaker-Levy 9 in 1994 after breaking up under the influence of Jupiter's tidal forces during a previous pass in 1992.

البروز المدي Tidal force هو حدوث ركامين مائيين من بحار الكرة الأرضية يحدثان بفعل قوة جاذبية الشمس والقمر. وطالما تدور الكرة الأرضية حول محورها كل يوم فهذان البروزان يتحركان فوق سطح الارض وينتجان المد والجزر .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الشرح

Figure 4: The Moon's gravity differential field at the surface of the Earth is known (along with another and weaker differential effect due to the Sun) as the Tide Generating Force. This is the primary mechanism driving tidal action, explaining two tidal equipotential bulges, and accounting for two high tides per day. In this figure, the Earth is the central blue circle while the Moon is far off to the right. The outward direction of the arrows on the right and left indicates that where the Moon is overhead (or at the nadir) its perturbing force opposes that between the earth and ocean.

When a body (body 1) is acted on by the gravity of another body (body 2), the field can vary significantly on body 1 between the side of the body facing body 2 and the side facing away from body 2. Figure 4 shows the differential force of gravity on a spherical body (body 1) exerted by another body (body 2). These so-called tidal forces cause strains on both bodies and may distort them or even, in extreme cases, break one or the other apart. The Roche limit is the distance from a planet at which tidal effects would cause an object to disintegrate because the differential force of gravity from the planet overcomes the attraction of the parts of the object for one another. These strains would not occur if the gravitational field were uniform, because a uniform field only causes the entire body to accelerate together in the same direction and at the same rate.

 Size and distance

The relationship of an astronomical body's size, to its distance from another body, strongly influences the magnitude of tidal force. The tidal force acting on an astronomical body, such as the Earth, is directly proportional to the diameter of that astronomical body and inversely proportional to the cube of the distance from another body producing a gravitational attraction, such as the Moon or the Sun. Tidal action on bath tubs, swimming pools, lakes, and other small bodies of water is negligible.

Figure 3: Graph showing how gravitational attraction drops off with increasing distance from a body

Figure 3 is a graph showing how gravitational force declines with distance. In this graph, the attractive force decreases in proportion to the square of the distance, while the slope relative to value decreases in direct proportion to the distance. This is why the gradient or tidal force at any point is inversely proportional to the cube of the distance.

The tidal force corresponds to the difference in Y between two points on the graph, with one point on the near side of the body, and the other point on the far side. The tidal force becomes larger, when the two points are either farther apart, or when they are more to the left on the graph, meaning closer to the attracting body.

For example, the Moon produces a greater tidal force on the Earth than the Sun, even though the Sun exerts a greater gravitational attraction on the Earth than the Moon, because the gradient is less.

Gravitational attraction is inversely proportional to the square of the distance from the source. The attraction will be stronger on the side of a body facing the source, and weaker on the side away from the source. The tidal force is proportional to the difference.

 Sun, Earth, and Moon

As expected, the table below shows that the distance from the Moon to the Earth, is the same as the distance from the Earth to the Moon. The Earth is 81 times more massive than the Moon but has roughly 4 times its radius. As a result, at the same distance, the tidal force of the Earth at the surface of the Moon is about 20 times stronger than that of the Moon at the Earth's surface.

Gravitational body causing tidal force		Body subjected to tidal force			Diameter and distance	Tidal force
Body	Mass (m)	Body	Radius (r)	Distance (d)	${\frac {2r}{d^{3}}}$	$Gm~{\frac {2r}{d^{3}}}$
Sun	1.99×1030 kg	Earth	6.37×106 m	1.50×1011 m	3.81×10−27 m−2	5.05×10−7 m⋅s−2
Moon	7.34×1022 kg	Earth	6.37×106 m	3.84×108 m	2.24×10−19 m−2	1.10×10−6 m⋅s−2
Earth	5.97×1024 kg	Moon	1.74×106 m	3.84×108 m	6.12×10−20 m−2	2.44×10−5 m⋅s−2
m is mass; r is radius; d is distance; 2r is the diameter G is the gravitational constant = 6.674×10−11 m3 kg−1 s−2

 آثار قوى المد والجزر

Figure 3: Saturn's rings are inside the orbits of its moons. Tidal forces prevented the material in the rings from coalescing gravitationally to form moons.

Figure 2: This simulation shows a star getting torn apart by the gravitational tides of a supermassive black hole.

 الصياغة الرياضية

Figure 6: Tidal force is responsible for the merge of galactic pair MRK 1034.

Figure 7: Graphic of tidal forces. The top picture shows the gravity field of a body to the right, the lower shows their residual once the field at the centre of the sphere is subtracted; this is the tidal force. See Figure 4 for a more detailed version

By Newton's law of universal gravitation and laws of motion, a body of mass m at distance R from the center of a sphere of mass M feels a force ${\vec {F}}_{g}$,

${\vec {F}}_{g}=-{\hat {r}}~G~{\frac {Mm}{R^{2}}}$

equivalent to an acceleration ${\vec {a}}_{g}$,

${\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}$

where ${\hat {r}}$ is a unit vector pointing from the body M to the body m (here, acceleration from m towards M has negative sign).

Consider now the acceleration due to the sphere of mass M experienced by a particle in the vicinity of the body of mass m. With R as the distance from the center of M to the center of m, let ∆r be the (relatively small) distance of the particle from the center of the body of mass m. For simplicity, distances are first considered only in the direction pointing towards or away from the sphere of mass M. If the body of mass m is itself a sphere of radius ∆r, then the new particle considered may be located on its surface, at a distance (R ± ∆r) from the centre of the sphere of mass M, and ∆r may be taken as positive where the particle's distance from M is greater than R. Leaving aside whatever gravitational acceleration may be experienced by the particle towards m on account of m's own mass, we have the acceleration on the particle due to gravitational force towards M as:

${\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{(R\pm \Delta r)^{2}}}$

Pulling out the R² term from the denominator gives:

${\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}~{\frac {1}{\left(1\pm {\frac {\Delta r}{R}}\right)^{2}}}$

The Maclaurin series of $1/(1\pm x)^{2}$ is $1\mp 2x+3x^{2}\mp \cdots$ which gives a series expansion of:

${\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}\pm {\hat {r}}~G~{\frac {2M}{R^{2}}}~{\frac {\Delta r}{R}}+\cdots$

The first term is the gravitational acceleration due to M at the center of the reference body $m$, i.e., at the point where $\Delta r$ is zero. This term does not affect the observed acceleration of particles on the surface of m because with respect to M, m (and everything on its surface) is in free fall. When the force on the far particle is subtracted from the force on the near particle, this first term cancels, as do all other even-order terms. The remaining (residual) terms represent the difference mentioned above and are tidal force (acceleration) terms. When ∆r is small compared to R, the terms after the first residual term are very small and can be neglected, giving the approximate tidal acceleration ${\vec {a}}_{t,{\text{axial}}}$ for the distances ∆r considered, along the axis joining the centers of m and M:

${\vec {a}}_{t,{\text{axial}}}\approx \pm {\hat {r}}~2\Delta r~G~{\frac {M}{R^{3}}}$

When calculated in this way for the case where ∆r is a distance along the axis joining the centers of m and M, ${\vec {a}}_{t}$ is directed outwards from to the center of m (where ∆r is zero).

Tidal accelerations can also be calculated away from the axis connecting the bodies m and M, requiring a vector calculation. In the plane perpendicular to that axis, the tidal acceleration is directed inwards (towards the center where ∆r is zero), and its magnitude is ${\textstyle {\frac {1}{2}}\left|{\vec {a}}_{t,{\text{axial}}}\right|}$ in linear approximation as in Figure 4.

The tidal accelerations at the surfaces of planets in the Solar System are generally very small. For example, the lunar tidal acceleration at the Earth's surface along the Moon–Earth axis is about 1.1×10⁻⁷ g, while the solar tidal acceleration at the Earth's surface along the Sun–Earth axis is about 0.52×10⁻⁷ g, where g is the gravitational acceleration at the Earth's surface. Hence the tide-raising force (acceleration) due to the Sun is about 45% of that due to the Moon. The solar tidal acceleration at the Earth's surface was first given by Newton in the Principia.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 انظر أيضا

• المد والجزر
• جاذبية
• Amphidromic point
• Disrupted planet
• Galactic tide
• Tidal resonance
• Tidal stripping
• Tidal tensor
• Spacetime curvature

 المصادر

• مؤمن, عبد الأمير (2006). قاموس دار العلم الفلكي. بيروت، لبنان: دار العلم للملايين. {{cite book}}: Cite has empty unknown parameter: |طبعة أولى coauthors= (help)

 وصلات خارجية

• Gravitational Tides by J. Christopher Mihos of Case Western Reserve University
• Audio: Cain/Gay – Astronomy Cast Tidal Forces – July 2007.
• Gray, Meghan; Merrifield, Michael. "Tidal Forces". Sixty Symbols. Brady Haran for the University of Nottingham.
• Pau Amaro Seoane. "Stellar collisions: Tidal disruption of a star by a massive black hole". Retrieved 2018-12-28.
• Myths about Gravity and Tides by Mikolaj Sawicki of John A. Logan College and the University of Colorado.
• Tidal Misconceptions by Donald E. Simanek