معين الأوجه Rhombohedron

Rhombohedron

Type	prism
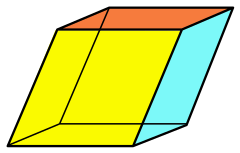
Faces	6 rhombi
Edges	12
Vertices	8
Symmetry group	C_i , [2⁺,2⁺], (×), order 2
Properties	convex, equilateral, zonohedron, parallelohedron

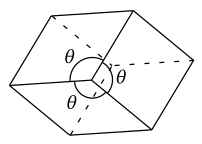
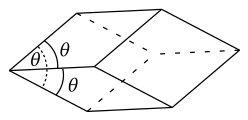
In geometry, a rhombohedron (also called a rhombic hexahedron^[1]^[2] or, inaccurately, a rhomboid^[أ]) is a special case of a parallelepiped in which all six faces are congruent rhombi.^[3] It can be used to define the rhombohedral lattice system, a honeycomb with rhombohedral cells. A rhombohedron has two opposite apices at which all face angles are equal; a prolate rhombohedron has this common angle acute, and an oblate rhombohedron has an obtuse angle at these vertices. A cube is a special case of a rhombohedron with all sides square.

حالات خاصة

The common angle at the two apices is here given as خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} . There are two general forms of the rhombohedron: oblate (flattened) and prolate (stretched).


Oblate rhombohedron, note there is a mistake in the labelling of angles here. All angles labeled theta should be on the acute angles. Here, two are on the obtuse and one is on the acute.	Prolate rhombohedron

In the oblate case خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta > 90^\circ} and in the prolate case خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta < 90^\circ} . For خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = 90^\circ} the figure is a cube.

Certain proportions of the rhombs give rise to some well-known special cases. These typically occur in both prolate and oblate forms.

الشكل	مكعب	√2 Rhombohedron	Golden Rhombohedron
Angle constraints	خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=90^\circ}
Ratio of diagonals	1	√2	Golden ratio
Occurrence	Regular solid	Dissection of the rhombic dodecahedron	Dissection of the rhombic triacontahedron

هندسة الجواسئ

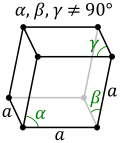
For a unit (i.e.: with side length 1) rhombohedron,^[4] with rhombic acute angle خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta~} , with one vertex at the origin (0, 0, 0), and with one edge lying along the x-axis, the three generating vectors are

e₁ : خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \biggl(1, 0, 0\biggr),}

e₂ :

{\biggl (}\cos \theta ,\sin \theta ,0{\biggr )},

e₃ :

{\biggl (}\cos \theta ,{\cos \theta -\cos ^{2}\theta  \over \sin \theta },{{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }} \over \sin \theta }{\biggr )}.

The other coordinates can be obtained from vector addition^[5] of the 3 direction vectors: e₁ + e₂ , e₁ + e₃ , e₂ + e₃ , and e₁ + e₂ + e₃ .

The volume خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} of a rhombohedron, in terms of its side length خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and its rhombic acute angle خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta~} , is a simplification of the volume of a parallelepiped, and is given by

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = a^3(1-\cos\theta)\sqrt{1+2\cos\theta} = a^3\sqrt{(1-\cos\theta)^2(1+2\cos\theta)} = a^3\sqrt{1-3\cos^2\theta+2\cos^3\theta}~.}

We can express the volume خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} another way :

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = 2\sqrt{3} ~ a^3 \sin^2\left(\frac{\theta}{2}\right) \sqrt{1-\frac{4}{3}\sin^2\left(\frac{\theta}{2}\right)}~.}

As the area of the (rhombic) base is given by خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^2\sin\theta~} , and as the height of a rhombohedron is given by its volume divided by the area of its base, the height خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} of a rhombohedron in terms of its side length خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and its rhombic acute angle خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} is given by

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle h = a~{(1-\cos\theta)\sqrt{1+2\cos\theta} \over \sin\theta} = a~{\sqrt{1-3\cos^2\theta+2\cos^3\theta} \over \sin\theta}~.}

Note:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle h = a~z} ₃ , where خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} ₃ is the third coordinate of e₃ .

The body diagonal between the acute-angled vertices is the longest. By rotational symmetry about that diagonal, the other three body diagonals, between the three pairs of opposite obtuse-angled vertices, are all the same length.

العلاقة بـ orthocentric tetrahedra

Four points forming non-adjacent vertices of a rhombohedron necessarily form the four vertices of an orthocentric tetrahedron, and all orthocentric tetrahedra can be formed in this way.^[6]

Rhombohedral lattice

The rhombohedral lattice system has rhombohedral cells, with 6 congruent rhombic faces forming a trigonal trapezohedron^{[بحاجة لمصدر]}:

ملاحظات

^ More accurately, rhomboid is a two-dimensional figure.

المراجع

^ Miller, William A. (January 1989). "Maths Resource: Rhombic Dodecahedra Puzzles". Mathematics in School. 18 (1): 18–24. JSTOR 30214564.
^ Inchbald, Guy (July 1997). "The Archimedean honeycomb duals". The Mathematical Gazette. 81 (491): 213–219. doi:10.2307/3619198. JSTOR 3619198.
^ Coxeter, HSM. Regular Polytopes. Third Edition. Dover. p.26.
^ Lines, L (1965). Solid geometry: with chapters on space-lattices, sphere-packs and crystals. Dover Publications.
^ "Vector Addition". Wolfram. 17 May 2016. Retrieved 17 May 2016.
^ Court, N. A. (October 1934), "Notes on the orthocentric tetrahedron", American Mathematical Monthly 41 (8): 499–502, doi:10.2307/2300415 .

External links

?

[3] More accurately, rhomboid is a two-dimensional figure.

[1] Miller, William A. (January 1989). "Maths Resource: Rhombic Dodecahedra Puzzles". Mathematics in School. 18 (1): 18–24. JSTOR 30214564.

[2] Inchbald, Guy (July 1997). "The Archimedean honeycomb duals". The Mathematical Gazette. 81 (491): 213–219. doi:10.2307/3619198. JSTOR 3619198.

[4] Coxeter, HSM. Regular Polytopes. Third Edition. Dover. p.26.

[:0-5] Lines, L (1965). Solid geometry: with chapters on space-lattices, sphere-packs and crystals. Dover Publications.

[6] "Vector Addition". Wolfram. 17 May 2016. Retrieved 17 May 2016.

[7] Court, N. A. (October 1934), "Notes on the orthocentric tetrahedron", American Mathematical Monthly 41 (8): 499–502, doi:10.2307/2300415 .

[1]

[2]

[أ]

[3]

[4]

[5]

[6]