مبرهنة نورتون

تحليل خطي للشبكات
العناصر
المكونات
دوائر التوالي والتوازي
تحويلات المعاوقة
مبرهنات المولد	مبرهنات الشبكة
أساليب تحليل الشبكات
Two-port parameters

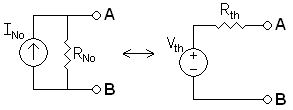
مبرهنة نورتون Norton's theorem، للشبكات الإلكترونية الخطية، ويعرف في اوروبا باسم مبرهنة ماير-نورتون، تنص على أن أي مجموعة مصادر جهد، مصادر تيار، و مقاومات لها محطتين طرفيتن تعادل مصدر التيار القياسي، I، بالتوازي مع مقاوم واحد، R. لأنظمة التيار المتردد أحادي التردد يمكن أيضا تطبيق النظرية على المعاوقات، وليس فقط على المقاومات. ويستخدم معادل نورتون ليمثل أي شبكة لمصادر خطية ومعاوقات، عند تردد معين. وتتكون الدائرة من مصدر تيار قياسي بالتوازي مع معاوق قياسي (أو مقاوم لدوائر غير تفاعلية).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

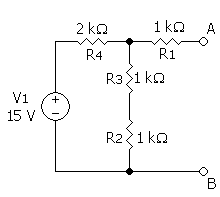
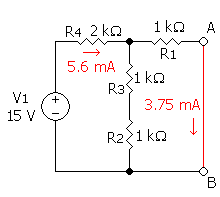
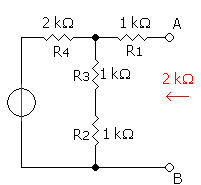
 مثال على دائرة معادل نورتون

Step 0: The original circuit

Step 1: Calculating the equivalent output current

Step 2: Calculating the equivalent resistance

Step 3: The equivalent circuit

In the example, the total current I_total is given by:

$I_{\mathrm {total} }={15\mathrm {V} \over 2\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \|(1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega )}=5.625\mathrm {mA}$

The current through the load is then, using the current divider rule:

$I={1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \over (1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega )}\cdot I_{\mathrm {total} }$

$=2/3\cdot 5.625\mathrm {mA} =3.75\mathrm {mA}$

$R=1\,\mathrm {k} \Omega +2\,\mathrm {k} \Omega \|(1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega )=2\,\mathrm {k} \Omega$

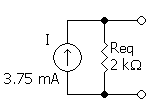
So the equivalent circuit is a 3.75 mA current source in parallel with a 2 kΩ resistor.

 التحويل إلى معادل ثيڤنين

$R_{Th}=R_{No}\!$

$V_{Th}=I_{No}R_{No}\!$

$V_{Th}/R_{Th}=I_{No}\!$

 انظر أيضا

• مبرهنة ثيڤنين

 وصلات خارجية

• Origins of the equivalent circuit concept
• Norton's theorem at allaboutcircuits.com