مبرهنة بايز

مبرهنة بايز هي إحدى نتائج نظرية الإحتمالات الهامة التي تعطي التوزيع الاحتمالي الشرطي للمتغير العشوائي A مع العلم بالمتغير العشوائي B, وذلك بدلالة التوزيع الاحتمالي الشرطي للمتغير العشوائي B مع العلم ب A والتوزع الاحتمالي للمتغيرين A وB.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 برهان مبدئي لمبرهنة بايز

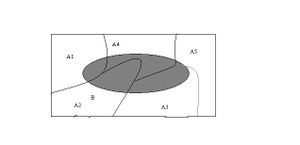
لنفرض أن الأحداث A1 و A2 و A3 و A4 و A5 ... تشكل تجزيئا لفضاء العينة S . أي أن A1 و A2 و A3 و A4 و A5 مجموعات جزئية من فضاء العينة S متنافية مثنى مثنى (لا يوجد تقاطع بين أي اثنين منها, واجتماعها جميعها يشكل فضاء العينة بكامله). لنفرض أن حدثا ضمن فضاء العينة B (المنطقة المظللة) فإن :

$B=(S\cap B)=()\cap B=(A1\cap B)\cup (A2\cap B)\cup (A3\cap B)\cup (A4\cap B)\cup (A5\cap B)$

و بما أن A1 و A2 و A3 و A4 و A5 متنافية مثنى مثنى فإن الأحداث $B\cap Ai$ متنافية أيضا مثنى :

$P(B)=P(A1\cap B)+P(A2\cap B)+P(A3\cap B)+P(A4\cap B)+P(A5\cap B)$

باستخدام علاقة الاحتمال الشرطي :

$P(B)=P(B|A1)P(A1)+P(B|A2)P(A2)+P(B|A3)P(A3)+P(B|A4)P(A4)+P(B|A5)P(A5)$

 مقولات مبرهنة بايز

تقوم مبرهنة بايز بربط الاحتمالات الشرطية conditional و الاحتمالات الحافية marginal probabilities, لكي نقوم باستنتاج هذه المبرهنة, لا بد لنا أن نبدأ من تعريف الاحتمال الشرطي:

$P(A|B)P(B)=P(A\cap B)=P(B|A)P(A)\,$

و هو ما يقرأ(جداء الاحتمال الشرطي ل A بمعرفة B في احتمال B) يعطي احتمال حدوث A وB معا وهو يساوي أيضا (جداء الاحتمال الشرطي ل B بمعرفة A في احتمال A).

باعتبار P(B) ليس معدوما نقوم بقسمة طرفي المعادلة السابقة عليه:

$P(A|B)={\frac {P(B|A)P(A)}{P(B)}}$

و هو نص ما يعرف عادة بمبرهنة بايز .

تقرأ : " الاحتمال الشرطي للحدث A بمعرفة الحدث B يساوي إلى احتمال B بمعرفة A مضروبا باحتمال A مقسوما على احتمال B . "