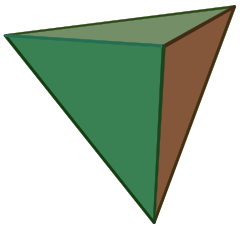
رباعي الأسطح
| Tetrahedron معتاد | |
|---|---|
 (انقر هنا لنموذج دوار) | |
| Type | جامد أفلاطوني |
| العناصر | F = 4, E = 6 V = 4 (χ = 2) |
| الأوجه والحواف | 4{3} |
| رمز شلافلي | {3,3} and s{2,2} |
| Wythoff symbol | 3 | 2 3 | 2 2 2 |
| Coxeter-Dynkin | |
| التماثل | Td or (*332) |
| References | U01, C15, W1 |
| الخصائص | محدب معتاد deltahedron |
| زاوية ثنائية الأوجه | 70.528779° = arccos(1/3) |
 3.3.3 (Vertex figure) |
 Self-dual (dual polyhedron) |
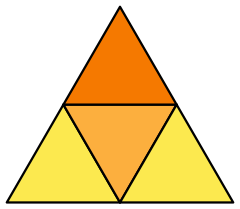 Net | |
رباعي الأسطح أو رباعي الأوجه هو متعدد أوجه مؤلف من أربعة وجوه مثلثية ، أما رباعي الوجوه المنتظم فهو رباعي وجوه تكون وجوهه مثلثات منتظمة. ويمكن تسميته هرم ثلاثي.
الإحداثيات الكارتيزية لرباعي الأسطح المعتاد
الإحداثيات الكارتيزية التالية تعرف رؤوس رباعي أسطح طول حده 2√2، متمركز في المركز:
- (1, 1, 1)
- (−1, −1, 1)
- (−1, 1, −1)
- (1, −1, −1)
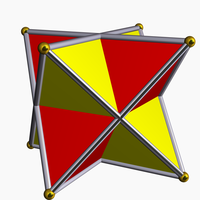
The compound of two tetrahedra shows the regular tetrahedron exists as two alternate sets of vertices of the cube.

:* الدوران
:* التطبيق والفرد
:* الشفافية
:* أهمهم: الرؤية المجسمة، أفضل مسافة للنظر هي 50-70 سم حين تنظر إلى الدقة الكاملة للصورة.
صيغ رباعي الأسطح المعتاد
لرباعي الأسطح المنتظم، الذي طول حده :
| مساحة مستوى القاعدة | |
| مساحة السطح[1] | |
| الارتفاع | |
| الحجم[1] | |
| الزاوية بين حافة ووجه | (تقريباً 54.736°) |
| الزاوية بين وجهين[1] | (تقريباً 70.529°) |
| الزاوية بين القطع الموصلة بين المركز والرؤوس [2], [3] | (تقريباً 109.471°) |
| الزاوية الصلبة عند رأس مقابل لوجه | (تقريباً 0.55129 steradians) |
| نصف قطر الكرة المحيطة[1] | |
| نصف قطر الكرة الداخلية المماسة للأوجه[1] | |
| نصف قطر midsphere المماسة للحواف[1] | |
| نصف قطر الكرات الخارجية | |
| المسافة إلى مركز exsphere من رأس |
الحجم
The volume of a tetrahedron is given by the pyramid volume formula:
where is the area of the base and h the height from the base to the apex. This applies for each of the four choices of the base, so the distances from the apexes to the opposite faces are inversely proportional to the areas of these faces.
For a tetrahedron with vertices a = (a1, a2, a3), b = (b1, b2, b3), c = (c1, c2, c3), and d = (d1, d2, d3), the volume is (1/6)·|det(a−b, b−c, c−d)|, or any other combination of pairs of vertices that form a simply connected graph. This can be rewritten using a dot product and a cross product, yielding
If the origin of the coordinate system is chosen to coincide with vertex d, then d = 0, so
where a, b, and c represent three edges that meet at one vertex, and is a scalar triple product. Comparing this formula with that used to compute the volume of a parallelepiped, we conclude that the volume of a tetrahedron is equal to 1/6 of the volume of any parallelepiped which shares with it three converging edges.
The triple scalar can be represented by the following determinants:
- or where is expressed as a row or column vector etc.
- ولذلك
- where etc.
- الذي يعطينا
- ,
where are the plane angles occurring in vertex d. The angle is the angle between the two edges connecting the vertex d to the vertices b and c. The angle does so for the vertices a and c, while is defined by the position of the vertices a and b.
Given the distances between the vertices of a tetrahedron the volume can be computed using the Cayley–Menger determinant:
where the subscripts تمثل القمم and هي المسافة الزوجية بينهم —أي طول الحافة الرابطة بين قمتين. القيمة السالبة للمحددة تعني أن رباعي الأسطح لا يمكن إنشاؤه بالمسافات المعطاة. هذه الصيغة، أحياناً تسمى صيغة تارتاليا، تعود في الأساس إلى الرسام پييرو دلا فرانشسكا في القرن 15، كمناظر ثلاثي الأبعاد لـصيغة هيرون، من القرن الأول، لمساحة مثلث.[2]
صيغة من نمط هيرون لحجم رباعي الأسطح
If U, V, W, u, v, w are lengths of edges of the tetrahedron (first three form a triangle; u opposite to U and so on), then[3]
حيث
المسافة بين الحواف
Any two opposite edges of a tetrahedron lie on two skew lines. If the closest pair of points between these two lines are points in the edges, they define the distance between the edges; otherwise, the distance between the edges equals that between one of the endpoints and the opposite edge. Let d be the distance between the skew lines formed by opposite edges a and b − c as calculated in.[4] Then another volume formula is given by
خصائص رباعي الأسطح العام
المزيد من الصيغ المتجهية في رباعي الأسطح العام
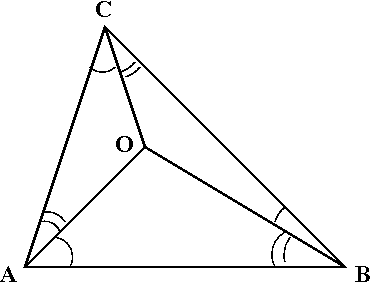
If OABC forms a general tetrahedron with a vertex O as the origin and vectors a, b and c represent the positions of the vertices A, B, and C with respect to O, then the radius of the insphere is given by[citation needed]:
ونصف قطر الدائرة المحيطة يؤخذ من:
which gives the radius of the twelve-point sphere:
where:
In the formulas throughout this section, the scalar a2 represents the inner vector product a·a; similarly b2 and c2.
المواقع المتجهية لمختلف المراكز هي كالتالي:
The centroid
The incenter
مركز الدائرة المحيطة
نقطة مونج
علاقات خط اويلر هي:
حيث T هي مركز الإثنتي عشر نقطة.
أيضاً:
و:
علاقات هندسية
A tetrahedron is a 3-simplex. Unlike the case of the other Platonic solids, all the vertices of a regular tetrahedron are equidistant from each other (they are the only possible arrangement of four equidistant points in 3-dimensional space).
رباعي الأسطح هو هرم مثلثي، ورباعي الأسطح المنتظم هو self-dual.
A regular tetrahedron can be embedded inside a cube in two ways such that each vertex is a vertex of the cube, and each edge is a diagonal of one of the cube's faces. For one such embedding, the Cartesian coordinates of the vertices are
- (+1, +1, +1);
- (−1, −1, +1);
- (−1, +1, −1);
- (+1, −1, −1).
عديدات أسطح ذات علاقة
A truncation process applied to the tetrahedron produces a series of uniform polyhedra. Truncating edges down to points produces the octahedron as a rectified tetahedron. The process completes as a birectification, reducing the original faces down to points, and producing the self-dual tetrahedron once again. قالب:Tetrahedron family
This polyhedron is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane.
 {3,3} |
 {3,4} |
 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3,9} |
رباعيات الأسطح المتقاطعة
المنظور
منظورات رباعيات الأسطح المنتظمة
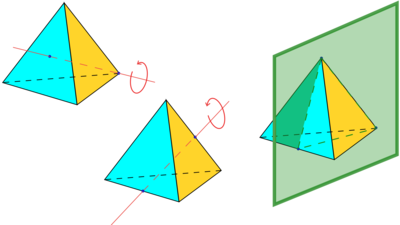
قمم المكعب can be grouped into two groups of four, each forming a regular tetrahedron (see above, and also animation, showing one of the two tetrahedra in the cube). The symmetries of a regular tetrahedron correspond to half of those of a cube: those that map the tetrahedra to themselves, and not to each other.
رباعي الأسطح هم المجسم الأفلاطوني الوحيد الذي لا يُرسل mapped إلى نفسه بواسطة point inversion.
قانون الجيوب لرباعيات الأسطح وفراغ كل أشكال رباعيات الأسطح
التطبيقات

انظر أيضاً
- Boerdijk–Coxeter helix
- Caltrop
- Demihypercube
- Disphenoid — a tetrahedron with mirror symmetry
- Hill tetrahedron
- Simplex
- Tetra-Pak
- Tetrahedral kite
- Tetrahedral molecular geometry
- Tetrahedral number
- Triangular dipyramid — constructed by joining two tetrahedra along one face
الهامش
- ^ أ ب ت ث ج ح Coxeter, H. S. M.: Regular Polytopes (Methuen and Co., 1948). Table I(i).
- ^ http://www.mathpages.com/home/kmath424.htm
- ^ W. Kahan, "What has the Volume of a Tetrahedron to do with Computer Programming Languages?", [1], pp. 16-17.
- ^ http://en.wikipedia.org/wiki/Skew_lines#Distance_between_two_skew_lines</a>
وصلات خارجية
| Tetrahedron
]].- F. M. Jackson and Eric W. Weisstein, Tetrahedron at MathWorld.
- Eric W. Weisstein, Monge point at MathWorld.
- Eric W. Weisstein, Euler points at MathWorld.
- The Uniform Polyhedra
- Tetrahedron: Interactive Polyhedron Model
- K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Piero della Francesca's formula for tetrahedron volume at MathPages
- Free paper models of a tetrahedron and many other polyhedra
- An Amazing, Space Filling, Non-regular Tetrahedron that also includes a description of a "rotating ring of tetrahedra", also known as a kaleidocycle.
- Tetrahedron Core Network Application of a tetrahedral structure to create resilient partial-mesh data network
- Explicit exact formulas for the inertia tensor of an arbitrary tetrahedron in terms of its vertex coordinates
- The inertia tensor of a tetrahedron