تكامل
في علم الرياضيات، تعتبر مكاملة الدالة نوعاً من التعميم لكميات قابلة للتجزئة مثل :المساحة أو الحجم أو الكتلة أو أي مجموع لعناصر متناهية في الصغر.
بالرغم من تعدد التعاريف المستخدمة للتكامل وتعدد طرق استخدامه فإن نتيجة هذه الطرق جميعها متشابهة وجميع التعاريف تؤدي في النهاية إلى المعنى ذاته.
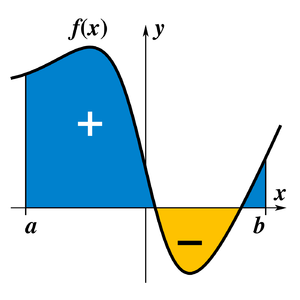
يمكن اعتبار تكامل دالة حقيقية مستمرة ذات قيم موجبة لمتغير حقيقي بين قيمة حدية دنيا و قيمة حدية عليا هي المساحة المحصورة بين المستقيمين الرأسيين :
x=a, x=b و المحور x و المنحني المحدد بالدالة ، يمكن صياغة ذلك بشكل رياضي:
ويرمز لهذه العملية حسب اصطلاح لورينتز :
.
النقطة الأساسية في التكامل تأتي من المبرهنة الأساسية في التكامل و التي تنص على أن مشتق تابع المساحة تحت منحني الدالة هو الدالة نفسها . بالتالي اذا عرفنا دالة تربط القيمة x يقيمة المساحة المحدودة بين منحني الدالة و محور السينات و من الجهة الخرى محدودة بمحور العينات و المستقيم X=x ، تدعى هذه الدالة ب دالة المساحة و مشتقها هو الدالة نفسها ، لذلك ندعو تابع المساحة عكس الإشتقاق أو التابع الأصلي للدالة .
يقوم حساب التكامل على ايجاد التابع الأصلي للدالة التي نريد القيام بمكاملتها .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
التاريخ
التكامل قبل اكتشاف التفاضل
نيوتون ولايبنتس
وقد عرض جوتفريد لايبنتز، في 13 نوفمبر 1675، أول عملية تكامل لحساب المساحة تحت منحنى الدالة ص = د(س).
يوجد عدة انواع للتكامل منها: التكامل بالتجزيء، التكامل بالتعويض، التحويل إلى الكسور الجزئية، الاختزال المتتالي.
خصائص التكامل
الخطية
Numerical quadrature
 مقالة مفصلة: التكامل الرقمي
مقالة مفصلة: التكامل الرقمي
The goals of numerical integration are accuracy, reliability, efficiency, and generality. Sophisticated methods can vastly outperform a naive method by all four measures (Dahlquist & Björck 2008; Kahaner, Moler & Nash 1989; Stoer & Bulirsch 2002). Consider, for example, the integral
which has the exact answer 94⁄25 = 3.76. (In ordinary practice the answer is not known in advance, so an important task — not explored here — is to decide when an approximation is good enough.) A “calculus book” approach divides the integration range into, say, 16 equal pieces, and computes function values.
Spaced function values x −2.00 −1.50 −1.00 −0.50 0.00 0.50 1.00 1.50 2.00 f(x) 2.22800 2.45663 2.67200 2.32475 0.64400 −0.92575 −0.94000 −0.16963 0.83600 x −1.75 −1.25 −0.75 −0.25 0.25 0.75 1.25 1.75 f(x) 2.33041 2.58562 2.62934 1.64019 −0.32444 −1.09159 −0.60387 0.31734
Quadrature method cost comparison الطريقة Trapezoid رومبرگ Rational گاوس Points 1048577 257 129 36 Rel. Err. −5.3×10−13 −6.3×10−15 8.8×10−15 3.1×10−15 القيمة
انظر أيضاً
المصادر
- Apostol, Tom M. (1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd ed.), Wiley, ISBN 978-0-471-00005-1
- Bourbaki, Nicolas (2004), Integration I, Springer Verlag, ISBN 3-540-41129-1. In particular chapters III and IV.
- Burton, David M. (2005), The History of Mathematics: An Introduction (6th ed.), McGraw-Hill, p. p. 359, ISBN 978-0-07-305189-5
- Cajori, Florian (1929), A History Of Mathematical Notations Volume II, Open Court Publishing, pp. 247–252, ISBN 978-0-486-67766-8, http://www.archive.org/details/historyofmathema027671mbp
- Dahlquist, Germund; Björck, Åke (2008), "Chapter 5: Numerical Integration", Numerical Methods in Scientific Computing, Volume I, Philadelphia: SIAM, http://www.mai.liu.se/~akbjo/NMbook.html
- Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN 978-0-471-80958-6
- Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, p. §231, http://books.google.com/books?id=TDQJAAAAIAAJ
Available in translation as Fourier, Joseph (1878), The analytical theory of heat, Freeman, Alexander (trans.), Cambridge University Press, pp. pp. 200–201, http://www.archive.org/details/analyticaltheory00fourrich - Heath, T. L., ed. (2002), The Works of Archimedes, Dover, ISBN 978-0-486-42084-4, http://www.archive.org/details/worksofarchimede029517mbp
(Originally published by Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.) - Hildebrandt, T. H. (1953), "Integration in abstract spaces", Bulletin of the American Mathematical Society 59 (2): 111–139, ISSN 0273-0979, http://projecteuclid.org/euclid.bams/1183517761
- Kahaner, David; Moler, Cleve; Nash, Stephen (1989), "Chapter 5: Numerical Quadrature", Numerical Methods and Software, Prentice Hall, ISBN 978-0-13-627258-8
- Leibniz, Gottfried Wilhelm (1899), Gerhardt, Karl Immanuel, ed., Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller, http://name.umdl.umich.edu/AAX2762.0001.001
- Miller, Jeff, Earliest Uses of Symbols of Calculus, http://members.aol.com/jeff570/calculus.html, retrieved on 2007-06-02
- O’Connor, J. J.; Robertson, E. F. (1996), A history of the calculus, http://www-history.mcs.st-andrews.ac.uk/HistTopics/The_rise_of_calculus.html, retrieved on 2007-07-09
- Rudin, Walter (1987), "Chapter 1: Abstract Integration", Real and Complex Analysis (International ed.), McGraw-Hill, ISBN 978-0-07-100276-9
- Saks, Stanisław (1964), Theory of the integral (English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised ed.), New York: Dover, http://matwbn.icm.edu.pl/kstresc.php?tom=7&wyd=10&jez=
- Stoer, Josef; Bulirsch, Roland (2002), "Chapter 3: Topics in Integration", Introduction to Numerical Analysis (3rd ed.), Springer, ISBN 978-0-387-95452-3.
- W3C (2006), Arabic mathematical notation, http://www.w3.org/TR/arabic-math/
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
وصلات خارجية
- The Integrator by Wolfram Research
- Function Calculator from WIMS
- Mathematical Assistant on Web online calculation of integrals, allows to integrate in small steps (includes also hints for next step which cover techniques like by parts, substitution, partial fractions, application of formulas and others, powered by Maxima (software))
Online books
- Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
- Stroyan, K.D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
- Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
- Crowell, Benjamin, Calculus, Fullerton College, an online textbook
- Garrett, Paul, Notes on First-Year Calculus
- Hussain, Faraz, Understanding Calculus, an online textbook
- Kowalk, W.P., Integration Theory, University of Oldenburg. A new concept to an old problem. Online textbook
- Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
- Numerical Methods of Integration at Holistic Numerical Methods Institute
- P.S. Wang, Evaluation of Definite Integrals by Symbolic Manipulation (1972) - a cookbook of definite integral techniques