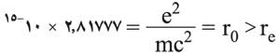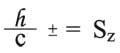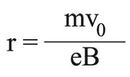إلكترون
 تقديرات نظرية لكثافة الإلكترون لأول بضعة مداريات إلكترونات ذرة الهيدروجين تظهر كمقاطع ذات كثافة احتمالات مميزة لونياً | |
| تركيب | جسيم ابتدائي |
|---|---|
| الأسرة | فرميون |
| المجموعة | لپتون |
| الجيل | أول |
| التفاعل | الجاذبية، كهرومغناطيسي، ضعيف |
| جسيم مضاد | پوزيترون |
| التنظير | ج. جونستون ستوني (1874) |
| اُكتـُشـِف | ج.ج. طومسون (1897) |
| الرمز | e−, β− |
| الكتلة | 9.10938215(45) × 10-31 kg[1][2] 5.48579909(27) × 10–4 u |
| الكتلة الكهربائية | –1.602176487(40) × 10–19 C[1][3] |
| سپين | ½ |
الإلكترون electron أو الكهرب هو جسيم دون ذري . تحيط الإلكترونات بالنواة المتكونة من بروتونات ونيترونات في شكل ترتيب إلكتروني. تم استحداث كلمة إلكترون في عام 1894 وتم اشتقاقها من المصطلح " Electric " كهربي والذي يساوي أصله الإغريقى كلمة عنبر، والذي كان يمكن الحصول على شحنة إلكتروستاتيكية منه عند مسحه بقطعة قماش. ويرجع المقطع الأخير "ون" إلى أنه يتشارك في معظم الجسيمات تحت الذرية التي استخدمت في كلمة أيون.
وكما تم التوضيح فإن الإلكترون له شحنة كهربية سالبة. وعندما يتحرك فإنه يولد تيارا كهربيا. ونظرا لأن الإلكترونات الموجودة في الذرة تحدد الطريقة التي تتفاعل بها الذرة مع الذرات الأخرى, فإنها تساهم بشدة في الخواص الكيميائية للعناصر وبذلك تلعب دورا رئيسيا في الكيمياء .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
نظرة عملية على الإلكترون
الإلكترون جسيم أولي elementary particle مستقر ذو شحنة كهربائية سالبة هي أصغر شحنة يمكن أن توجد في الطبيعة، ولذلك اتُّخذت واحدة كمية الكهرباء، وليست شحنة أي جسم سوى مضاعفات لها. أما كتلة الإلكترون فهي أصغر كتل الجسيمات المستقرة، وهي تعادل ما يقرب من جزء واحد من 1850 جزءاً من كتلة ذرة الهدروجين (أخف الذرات إطلاقاً(.
أظهرت دراسة بنية المادة أنها حبيبية، مؤلفة من ذرات atoms، كما تبيَّن أن الذرة مؤلفة من [[نواة nucleous صغيرة جداً (ذات قطر لا يتجاوز واحداً من مئة ألف من قطر الذرة) تشكل الجزء الأعظم من كتلة الذرة وشحنتها الكهربائية موجبة البروتونات، يدور حولها عدد من الإلكترونات يساوي عدد الشحنات الموجبة في النواة. ولذلك تعد الإلكترونات الوحدات الأساسية لبنية المادة، لكونها تشكل الغمامات الإلكترونية للذرات.
يمكن الحصول على الإلكترونات حرّة (غير مرتبطة بالذرات) في الخلاء بوساطة الإصدار الإلكتروني الحراري مثلاً (تسخين المادة). ويمكن تسريعها والاستفادة منها في كثير من التطبيقات العملية (الصمامات الإلكترونية، التلفاز، المجهر الإلكتروني، وغير ذلك). كما يُلجأ إلى تسريع حزم شديدة من الإلكترونات وإيصالها إلى طاقات عالية جداً بغية استخدامها في دراسة نوى الذرات والجسيمات الأولية (كما في السنكروترون synchrotron). وللإلكترون جسيم مضاد، كما للجسيمات الأولية الأخرى، وهو الإلكترون الموجب أو البوزترون positron (ويقال أيضاً البوزيتون positon) مضاد الإلكترون. ويصنف الإلكترون مع اللبتونات leptons، وهي الجسيمات التي لا تدخل مع الجسيمات الأخرى إلا في التأثيرات المتبادلة الكهرمغنطيسية والتأثيرات المتبادلة النووية الضعيفة. وهو يسهم في معظم التحولات التي تطرأ على الجسيمات الأولية.
وللإلكترونات صفات موجيّة، شأنها في ذلك شأن باقي الجسيمات الدقيقة، فهي تنعرج (تحيد) عند الذرات والجسيمات. ويستفاد من هذه الخواص في استخدام المجهر الإلكتروني لدراسة الأجسام البالغة الدقة التي تستحيل رؤيتها بالمجاهر الضوئية.
تصنيف الإلكترونات

الإلكترون عبارة عن أحد الجسيمات تحت النووية، ويطلق عليه أيضا اسم لپتون والذي يعتبر جسيما أساسيا (أي لا يمكن تكسيره للحصول على جسيمات أصغر).
وكلمة جسيم قد تكون محيرة عند استخدامها لدرجة ما، نظرا لأن ميكانيكا الكم أظهرت أن الإلكترون يسلك أيضا سلوك الموجات، أي أن له طبيعة مزدوجة، مثل ما يحدث في تجربة الانشقاق المزدوج أو بمعنى آخر يعتبر الإلكترون جسيم ذو طبيعة موجية.
النظرية الذرية
ميكانيكا الكم
خواص وسلوك الإلكترون
ترجع كلمة إلكترون غالبا إلى نيجاترون مشحون بشحنة كهربية سالبة مقدارها −1.6 × 10−19C وكتلة 9.11 × 10−31 كجم (0.511 MeV)
والذي يساوي تقريباً من كتلة البروتون. ويتم التعبير عن ذلك بالرمز e−. وقد قام كارل ديڤد أندرسون باستخدام نفس الكلمة كتعبير عن نيجاترون وپوزيترون. والپوزيترون له نفس الكتلة ونفس الشحنة ولكن بقيمة موجبة.
وتعتبر حركة الإلكترون حول النواة من الموضوعات التي لا يزال فيها جدال حاد. فلا يمكن اعتبار حركة الإلكترون كأي نوع من الحركات في علم الفيزياء نظرا لأن هذه الحركة ليست دائما موجودة, كما لو أن الإلكترون يختفي في بعض الأوقات أثناء دورانه حول النواة. وفي الوقت الحالي لا يمكن التنبؤ بمكان وسرعة الإلكترون في نفس الوقت.
وقد تم عرض هذا الفرض عن طريق مبدأ اللايقين هايزنبرج والذي يتم تطبيقه على الجسيمات التي لها طبيعة تماثل طبيعة الإلكترون, كما يمكن التعبير بصورة أخرى عن ذلك, كلما زادت دقة معرفة مكان الإلكترون كلما قلت دقة معرفة سرعته والعكس صحيح .
الإلكترون له دوران (أو التفاف) يساوى 1 / 2, والذي يثبت أنه فرميون, أي أنه جسيم يتبع إحصائيات فرمى ديراك.
وبينما توجد معظم الإلكترونات في الذرة, فإنه قد توجد بعض الإلكترونات التي تتحرك بمفردها في المادة, أو في شكل شعاع إلكتروني في الفراغ. فتتحرك الإلكترونات في الموصلات الفائقة على هيئة "أزواج كوبر" والتي تتزاوج أثناء حركتها بقرب حواف المادة عن طريق شبكة اهتزازية فيما يعرف بالفونون.
عندما تتحرك الإلكترونات, بعيدا عن النواة, في شكل شبكي فهذا يعرف بالكهرباء أو التيار الكهربائي.
على أن الكهرباء الساكنة, لا تعتبر سريانا للإلكترونات. ولكنها ترجع لأي جسم به عدد أقل أو أكبر من عدد الإلكترونات اللازم لعمل اتزان للشحنة الموجبة الموجودة في النواة. وعندما تكون الإلكترونات أكثر يكون الجسم سالب الشحنة, بينما يكون موجب الشحنة في حالة أن الإلكترونات أقل. ويكون الجسم متعادل الشحنة حينما يكون عدد الإلكترونات مساو لعدد البرتونات.
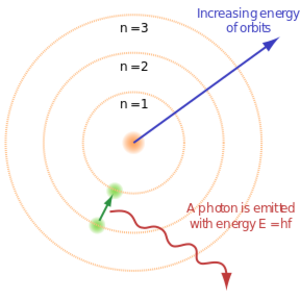
يمكن للإلكترون والپوزيترون أن يقضيا على بعضهما البعض لتكوين فوتون. وبالعكس فإن الفوتون الذي له طاقة عالية يمكن أن يتحول إلى إلكترون وبوزيترون بعملية يطلق عليها الإنتاج الزوجي.
الإلكترون جسيم أولي أي أنه لا يوجد له تركيب تفصيلي (لم تجد أي من التجارب العلمية حتى الآن أي تركيب تفصيلي له). وعلى هذا فإنه يوصف على أنه شبيه بالنقطة أي لا يوجد له حيز مكاني. وعند النظر بقرب أكثر للإلكترون فيمكن ملاحظة أن خواصه (الشحنة والكتلة) تتغير.
وهذا يحدث بصفة عامة لكل الجسيمات الأولية عند اقترابها من بعضها البعض في الفراغ, وعلى هذا فإن الخواص التي نشاهدها من بعيد تكون محصلة التأثيرات الحادثة في الفراغ.
يوجد ثابت فيزيائي يسمى نصف قطر الإلكترون التقليدي وقيمته 2.8179 × 10−15 م وقد تم الاستدلال على هذه القيمة من شحنة الإلكترون وهذا تم عن طريق النظرية التقليدية للديناميكا الحرارية وبدون وجود نظريات ميكانيكا الكم (أي أنه تصور قديم ولكنه مع ذلك لايزال يصلح للاستخدام في الحسابات).
تقترب سرعة الإلكترون في الفراغ من سرعة الضوء في الفراغ ولكن لا تصل إليها. وهذا راجع للنسبية الخاصة. وتأثير النسبية الخاصة مبني على كمية تعرف بجاما أو عامل لورينتز. وتكون جاما عبارة عن معادلة مبنية على سرعة الجسيم v وسرعة الضوء c وهي كالتالي:
كتلة الإلكترون وشحنته وأبعاده
تبلغ الكتلة السكونية للإلكترون وفق القياسات الحديثة القيمة
m0 =9.1083×10 -31كغ=0.548763×10 -3 وحدة كتلة ذرية (و ك ذ) (amu)
وتعادل هذه الكتلة الطاقة:
- m0c2 = 0.510976 مليون إلكترون ڤولت (م إ ف) (MeV)
حيث c: سرعة الضوء في الفراغ
أما شحنة الإلكترون فتبلغ القيمة:
e= 1.60206×10 -19 كولون = -4.80286×10 -10 وحدة كهرساكنة (و ك س) (esu)
ويمكن الحصول على تقدير تقريبي للحد الأعلى لنصف قطر الإلكترون re بافتراض أن كتلته كلها ذات منشأ كهرمغناطيسي، ويكون:
سبين الإلكترون وعزمه المغناطيسي الذاتي
أدخل جورج اولنبك وصمويل گودسميت مفهوم سبين الإلكترون (أو اندفاعه الزاوي الذاتي) لتفسير بعض الحقائق التجريبية ومنها تضاعف بعض الخطوط الطيفية. وقد افترض هذان العالمان وجود اندفاع زاوي ذاتي للإلكترون إضافة لاندفاعه الزاوي المداري الناتج من حركته حول النواة. وافترضا أن هذا الاندفاع ناشئ عن دوران الإلكترون حول نفسه (ومن هنا أتت تسميته بالإنجليزية spin). إلا أن النظريات الحديثة تميل إلى احتمال أن له بنية داخلية معقدة ما تزال مجهولة، وذلك على الرغم من عدم وجود أي دلائل تجريبية على بنية الإلكترون حتى اليوم. وقد وُجد أن لسبين الإلكترون القيمة
وh هي ثابت پلانك Planck ويساوي 6.6256×10-34 جول ثانية. كما وُجد أنه لا يمكن أن يكون لمسقط متجهة السبين على منحى معين (وليكن المحور z) سوى إحدى القيمتين
وهذا ما يعبر عنه عادة بأن سبين الإلكترون يساوي (مقدراً بواحدات )، وتخضع الإلكترونات بالتالي لإحصاء فرمي-ديراك Fermi- Dirac، شأنها في ذلك شأن باقي الجسيمات التي يساوي سبينها SZ أمثالاً فردية من والتي يطلق عليها اسم فِرميونات fermions. لما كان الإلكترون جسيماً مشحوناً كهربائياً فإن وجود اندفاع زاوي ذاتي (سبين) له يستدعي وجود مغنطيسي ذاتي μ. وتثبت التجربة وجود هذا العزم، وتبلغ قيمته
وتبلغ نسبة العزم المغنطيسي الذاتي إلى السبين ضعف قيمة نسبة العزم المغنطيسي المداري إلى عزم الاندفاع الزاوي المداري.
الإلكترون الموجب أوالبوزيترون
وهو الجسيم المضاد للإلكترون، وهو لا يمكن أن يوجد في الطبيعة إلا مدة زمنية قصيرة جداً. وله كتلة سكونية تساوي تماماً كتلة الإلكترون وشحنة كهربائية موجبة تساوي شحنة الإلكترون بالقيمة المطلقة، وله سبين يساوي سبين الإلكترون. وهو كالإلكترون جسيم مستقر، وسلوكه مشابه تماماً لسلوك الإلكترون إنما مدة حياته صغيرة جداً لا تتجاوز 10-7 ثانية بسبب فنائه بمجرد التقائه أحد الإلكترونات. فحين يلتقي البوزترون الإلكترون يفنى الجسيمان مولدين طاقة كهرمغنطيسية بصورة أشعة گاما (γ):
وتساوي الطاقة المنطلقة ما يكافئ كتلتي الجسيْمين من الطاقة أي 2mc2، وهي من رتبة المليون إلكترون فُلط. ويصدُر البوزترون في أثناء النشاط الإشعاعي بيتا β وفي تفاعلات الطاقة العالية، حيث تتحول طاقة أشعة گاما γ بجوار نوى الذرات إلى زوجين إلكترون وبوزترون.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
تأثير الحقل الكهربائي في حركة الإلكترون
لما كانت للإلكترونات شحنة كهربائية فهي تكتسب تسارعاً في الحقل الكهربائي. ولكون الشحنة النوعية للإلكترون كبيرة فإن تسارعه كبير حتى في الحقول الكهربائية الضعيفة. ويُحسب التسارع a الذي يكتسبه الإلكترون في الحقل الكهربائي E وفق قوانين المكانيك التقليدي من العلاقة:
أما السرعة V التي يكتسبها الإلكترون بفضل فرق كمون كهربائي V فتُحسب من مساواة الطاقة الكامنة التي يخسرها الإلكترون eV بالطاقة الحركية التي يكتسبها
وتكون السرعة المكتسبة:
فإذا وضعت قيمة للإلكترون في هذه العلاقة أمكن كتابة عبارة V بدلالة فرق الكمون V كما يلي:
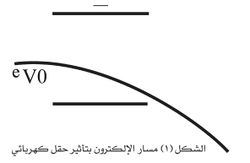
حيث تقدر V بالڤلط وv بالكيلو متر في الثانية. وتجدر الإشارة إلى أنه ابتداءً من سرعة معينة لا يجوز إهمال ازدياد الكتلة مع تزايد السرعة، وهو ما تمليه النظرية النسبية. وبالفعل حين يبلغ فرق الكمون المسرِّع 100 كيلو فلط يصبح الفرق بين السرعة المحسوبة وفق العلاقة (3) والسرعة الحقيقية من رتبة 20 بالمئة. أما إذا بلغ فرق الكمون مليون ڤلط فإن سرعة الإلكترون محسوبة وفق الميكانيك التقليدي (العلاقة 3) تبلغ 600 ألف كم/ثا في حين أنها في الواقع ليست سوى 282 ألف كم/ثا. أما إذا دخل إلكترون يتحرك بالسرعة V0 حقلاً كهربائياً مائلاً بالنسبة إلى V0، فإن متجهة سرعته الابتدائية هذه تضاف إلى متجهة السرعة v الناتجة من تأثير الحقل الكهربائي ويصبح مسار الإلكترون على شكل قطع مكافئ.
تأثير الحقل المغنطيسي في حركة الإلكترون
لما كان الإلكترون ذا شحنة كهربائية فإنه يخضع، حين يدخل مجال حقل تحريض مغنطيسي B بالسرعة V0، إلى قوة F عمودية على كل من منحني سرعته V0 ومنحى الحقل B. وتُعطى القوة هذه بالعلاقة المتجهية التالية:
فإذا كانت سرعة الإلكترون لدى دخوله مجال حقل التحريض عمودية على كان مقدار القوة مساوياً evB وكانت حركة الإلكترون وفق دائرة نصف قطرها
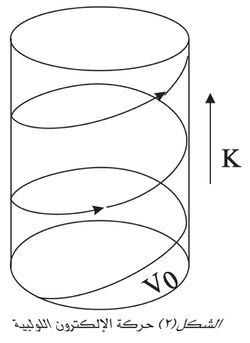
إن حقلاً مغنطيسياً ضعيفاً يمكن أن يؤدي إلى انحناءٍ ملحوظ في مسار الإلكترون: فمركبة الحقل المغنطيسي الأرضي الأفقية مثلاً تؤدي إلى جعل حركة الإلكترون المسرَّع بفرق كمون قدره 100 فلط حركة منحنية نصف قطرها 1.7 متراً. أما الحقل المغنطيسي الموازي لمنحى حركة الإلكترون فلا يؤثر في حركة الإلكترون إطلاقاً. وفي الحالة العامة يمكن تحليل سرعة الإلكترون إلى مركّبتين إحداهما عمودية على الحقل والأخرى موازية له. وتؤدي المركّبة العمودية إلى حركة الإلكترون الدائرية، في حين تؤدي المركّبة الموازية إلى حركة مستقيمة موازية للحقل. وتكون الحركة المحصّلة لولبية.
خواص الإلكترون الموجيّة
لتفسير الظواهر الموجية للجسيمات وضع لوي دي بْروُي Louis de Broglie عام 1924 فرضية مفادها أن الجسيمات ذات طبيعة مثنوية (جسيميةـ موجية). وبحسب هذه الفرضية تواكب كلَّ جسيم متحرك موجةٌ، تدعى موجة دي بروي، يعطى طولها λ بالعلاقة:
حيث p: اندفاع الجسيم (كمية حركته) وE: طاقته الحركية وh: ثابتة بلانك.
وبهذا تواكب الإلكترون ذا الطاقة الحركية 100 إلكترون فلط موجةٌ طولها 0.12 نانو متر (أي 0.12×10-9 متر أو 1.2 أنگستروم).
ولما كان هذا الطول من مرتبة المسافة بين الذرات في البلورات، فيمكن إذن توقع حدوث انعراج حزمة إلكترونات كهذه عند البلورات شبيه بانعراج الأشعة السينية عندها. وبالفعل فقد حصل داڤيسون C.J.Davisson وجيرْمَر L.H.Germer عام 1927 على انعراج حزمة إلكترونية على بلورة رقيقة من التوتياء.
حين تزداد طاقة الإلكترونات ينقص طول موجتها (العلاقة 5)، أما حين تزيد على حدود معينة (أكثر من 100 كيلو إلكترون ڤلط) فلا يعود طول الموجة المواكبة للإلكترون يتبع العلاقة البسيطة (5) ذاتها، إذ ينبغي حينئذٍ أخذ التصحيحات الناتجة عن النظرية النسبية بالحسبان. ويستفاد من إمكان إنقاص طول موجة الإلكترونات إلى حد بعيد في الكثير من التطبيقات المهمة، كالمجهر الإلكتروني.
الإلكترون في الكون
من المعروف أن عدد الإلكترونات الموجودة في الكون المعروف هو على الأقل 1079. وهذا الرقم مبني على أساس واحد إلكترون في المتر المكعب من الفضاء.
وبناء على نصف قطر الإلكترون التقليدي وبفروض تغليف الأجسام الكروية فإنه يمكن حساب كمية الإلكترونات التي يمكن أن تملأ الفراغ تقريبا 10130. على أن هذا الرقم أقل بكثير من نصف قطر الإلكترون التقليدي.
التطبيقات
الإلكترون في الصناعة
يتم استخدام شعاع الإلكترونات في اللحام والطبع الحجري .
تجارب الاكتشاف
تم اكتشاف طبيعة الإلكترون بواسطة روبرت ميليكان في تجربة قطرة الزيت في عام 1909 م.
استخدام الإلكترون في المعامل
المجهر الإلكتروني يستخدم لتكبير التفاصيل الدقيقة حتى 500,000 مرة. ويتم استخدام تأثير الكوانتم للإلكترونات في مجهر المسح الأنبوبي.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
الإلكترون في النظريات
في ميكانيكا الكم, تم وصف الإلكترون بواسطة معادلة ديراك. في النموذج القياسي لفيزياء الجسيمات فإن الإلكترون يكون ما يشبه المعطف مع (SU(2 مع نيوترونو الإلكترون حيث أنهما يتفاعلان خلال تفاعل الضعف. وللإلكترون شريكان أخران بنفس الشحنة ولكن بكتل مختلفة: موان وتاون.
معاكس المادة للإلكترون هو معاكس الجسيم, البوزيترون. والبوزيترون له نفس كمية الشحنة الموجودة في الإلكترون ولكن شحنته موجبة. وله نفس كتلة ودوران الإلكترون. وعندما يتقابل إلكترون وبوزيترون فإنهما يقضيا على بعضهما البعض, ويكونا 2 فوتون من أشعة جاما, وكل منها له شحنة 0.511 MeV ( 511 KeV ). راجع إبادة إلكترون-بوزيترون.
ويعتبر الإلكترون أيضا عنصرا أساسيا في الإلكتروماجنيتيزم, وهي نظرية مهمة في أنظمة المجهر.
البصريات الإلكترونية
وتشمل المبادئ العامة والعدسات الإلكترونية.
المبادئ العامة
تدرس البصريات الإلكترونية electron optics الشروطَ والقوانين اللازمة لتشكيل الحزم الإلكترونية أو الأيونية وانتشارها وتجميعها؛ ومعرفة هذه الشروط والقوانين ضرورية لتصميم الأجهزة البصرية الإلكترونية كالمجهر الإلكتروني والمطياف الكتلي ومسرِّعات الجسيمات المشحونة، والأنابيب التلفازية المستعملة على نطاق واسع في كثيرٍ من التقنيات والصناعات وفروع العلم.
تخضع الإلكترونات في حركتها، بسبب خواصها الجسيمية الموجيّة، لقوانين تشبه القوانين التي تخضع لها الأشعة الضوئية. إلا أنه على الرغم من هذا التشابه، توجد اختلافات عميقة تؤدي إلى صعوبة أكبر في تصميم الأجهزة البصرية الإلكترونية من ناحية، وتوفر من ناحية أخرى إمكانات كبيرة لدراسة ظواهر ذات أهمية بالغة، وتكمن هذه الاختلافات فيما يلي:
ـ ينتشر الشعاع الضوئي، عند خروجه من مصدر الإشعاع، بسرعة تميِّزه هي سرعة الضوء، في حين تخرج الإلكترونات من المادة التي تصدرها بسرعات صغيرة. وللحصول على حزم إلكترونية صالحة للاستعمال عملياً في الأجهزة الإلكترونية ينبغي تسريع هذه الإلكترونات، وهذا ما يتم التوصل إليه بالتأثير فيها بحقول كهربائية مناسبة.
ـ تعد مقدرة الفصل resolving power إحدى المميزات الأساسية للمجهر الضوئي، وهي محدودة من حيث المبدأ بطبيعة الضوء الموجيّة ذاتها. وتدل الدراسة النظرية لظاهرة انعراج الضوء diffraction على أن مقدرة الفصل الحدية للمجاهر هي:
حيث d: هي أصغر مسافة بين نقطتين يمكن فصلهما (أي تمييزهما) بوساطة المجهر، وλ: طول موجة الإشعاع الذي يضيئ الجسم المدروس بالمجهر، وn: قرينة انكسار الوسط الذي يوجد فيه الجسم المدروس، وα: زاوية فتحة المجهر aperture. ويدعى الجداء n sin α الفتحة العددية لجسمية المجهر وتبلغ قيمتها العظمى في أفضل المجاهر 6،.1 وتبلغ قيمة λ الوسطية للضوء المرئي 550 نانو متر تقريباً، مما يجعل أصغر مسافة فاصلة يمكن تمييزها بوساطة المجهر الضوئي 180 نانو متر على وجه التقريب. ولا يمكن تحسين مقدرة الفصل أكثر من ذلك إلا باستعمال أشعة ذات طول موجي أصغر. وهذا ما يمكن أن توفره الإلكترونات المتحركة بسرعة كبيرة في المجهر الإلكتروني، إذ إن طول الموجة المواكبة للإلكترون يعطى بالعلاقة (5) التي تبين أنه يمكن إنقاص طول موجة الإلكترون بزيادة طاقته الحركية أي بزيادة فرق الكمون المسرِّع للإلكترونات، وتراوح فروق الكمون المستعملة بين 50 كيلو فلط وعدة ملايين من الفلطات، مما يجعل طول موجة الإلكترون أصغر من طول موجة الضوء بآلاف المرات، وتصبح بذلك مقدرة الفصل في المجهر الإلكتروني أفضل منها في المجهر الضوئي بآلاف المرات.
ـ ينتشر شعاع الضوء المرئي عملياً من دون أي عائق في كثير من المواد الصلبة والسائلة والغازية التي توصف بأنها شفافة، أما الحزم الإلكترونية فلا يمكن أن تنتشر إلا في الخلاء. ولهذا السبب تكون كل الأجهزة البصرية الإلكترونية مفرغة من الهواء.
ـ ينتشر الشعاع الضوئي عادة وفق خط مستقيم ولا ينحرف عن مساره إلا عند السطح الفاصل بين الأوساط المختلفة أو نتيجة لتغير كثافة الوسط الذي ينتشر فيه. أما الحزم الإلكترونية المنتشرة بشكل مستقيم في الخلاء فتنحرف نتيجة لتأثرها بالحقول الكهربائية والمغنطيسية، وتصبح مسارات الإلكترونات، عموماً، مسارات منحنية في هذه الحقول.
العدسات الإلكترونية
إن تأثير الحقول العرضية (الكهربائية والمغنطيسية) في الإلكترونات يشبه تأثير المواشير الزجاجية في الأشعة الضوئية، إذ يقتصر فعل هذه الحقول على حرف الحزم الإلكترونية فحسب. أما تجميعها فيمكن أن يتم بوساطة الحقول الكهربائية والمغنطيسية التي تتصف بالتناظر الدوراني بالنسبة لمحور الجهاز البصري الإلكتروني. وتتميز هذه الحقول بأن درجة انحراف الإلكترونات فيها تزداد بازدياد البعد عن المحور المذكور. ويتم الحصول عليها بأجهزة خاصة تدعى العدسات تشبيهاً بعدسات البصريات الضوئية، ويُميَّز منها العدسات الكهربائية الساكنة والعدسات المغنطيسية. وليس من السهل تعيين مسار الإلكترونات في هذه الحقول (وهو أمر ضروري لتعيين وسطاء العدسة الأساسية كالبعد المحرقي (البؤري) والمستويات الأصلية) ذلك لأن شدة الحقول ليست ثابتة، كما هو الحال في الحقول المنتظمة، وإنما تتغير تغيراً مستمراً من نقطة لأخرى. ولإيجاد مسار الإلكترون في هذه الحالة يقسم الفضاء بين أي مسريين مشحونين إلى أقسام بوساطة عدد من سطوح سوية الكمون التي يعتمد عددها على الدقة المطلوبة. ثم يُحدد الانحراف الذي يعانيه الإلكترون من سطح سوية كمون إلى سطح آخر. ويتم، على هذا النحو، إيجاد مسار الإلكترون نقطة فنقطة بافتراض أنه يتحرك حركة مستقيمة بين نقطتين متتاليتين.
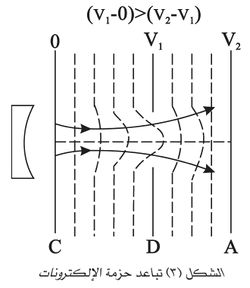
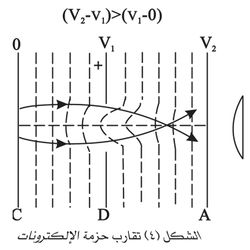
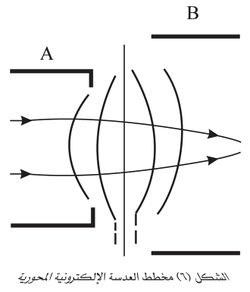
أـ العدسات الإلكترونية الكهرساكنة: تتألف العدسة الإلكترونية الكهرساكنة من مجموعة صفائح معدنية (مسارٍ) electrodes ذات فتحات دائرية تقع مراكزها على محور الجملة الإلكترونية البصرية. ويعتمد البعد المحرقي للعدسة على سرعة الإلكترونات التي تجتازها وعلى الوسطاء الهندسية للعدسة (أقطار الفتحات، ثخن الصفائح، المسافات بينها) وعلى الوسطاء الكهربائية (فروق الكمون بين المساري). إن أبسط عدسة إلكترونية كهرساكنة هي المؤلفة من صفيحة واحدة ذات فتحة مستديرة، وهي الصفيحة D في الشكل (3) التي توضع بين مسريين A وC مستويين ومتوازيين وفرق الكمون بينهما V2+ (باعتبار أن كمون المسرى C صفر). فإذا جعل كمون الصفيحة D مختلفاً عن قيمته في مكانها قبل وضعها فيه فإن شكل سطوح سوية الكمون وتوزعها بين A وC يتغيران، فبدلاً من أن تكون هذه السطوح مستوية متوازية ويكون انتشار الإلكترونات الناظمية عليها مستقيماً، تصبح سطوح سوية الكمون منحنية وتصبح حزمة الإلكترونات المتوازية إما متباعدة أو متقاربة حسبما يكون كمون الصفيحة D، وليكن V1 أكبر من V2-V1 (الشكل 3) أو أصغر منه (الشكل 4). وفي كلتا الحالتين يمكن التحكم في مدى تقارب الحزمة أو تباعدها بوساطة تغيير الكمون V1.
ثمة نوع آخر من العدسات الإلكترونية الكهرساكنة تتألف العدسة فيه من ثلاثة مسار A وB وC (الشكل 5). وغالباً ما يجعل للمسريين A وC الكمون نفسه (وتدعى العدسة عندئذٍ متناظرة) في حين يجعل كمون B أخفض. ويكون تقارب الحزمة الإلكترونية تابعاً للنسبة بين كمونات المساري.
أما العدسات المحورية فتتألف من مسريين أسطوانيين A وB بينهما فراغ صغير؛ يُجعل كمون المسريين موجباً بالنسبة إلى المهبط cathode الذي تصدر عنه حزمة الإلكترونات، ويُجعل كمون المسرى الثاني B أعلى من كمون الأول A (الشكل 6) وتكون الجملة متناظرة تماماً بالنسبة إلى سطح سوية الكمون الوسطي مما يؤدي إلى تغير جهة مركِّبة سرعة الإلكترون القطرية فجأة لدى الانتقال من النصف الأول (الأيسر في الشكل 6) إلى النصف الثاني (الأيمن). ولما كانت الإلكترونات المسرِّعة تقطع، في أثناء مرورها من العدسة، النصف الثاني بسرعة أكبر من السرعة التي تقطع بها النصف الأول، فهي تخضع لتأثير الحقل الكهربائي فيه في أثناء زمن أقل، مما يؤدي إلى أن تتقارب الحزمة الإلكترونية في النتيجة. ويمكن التحكم في قدرة العدسة على التجميع بتغيير كمون A وB.
ب ـ العدسات الإلكترونية المغنطيسية: وتتألف عادة من أسلاك ملفوفة على هيئة وشائع تُجعل لفاتها الدائرية متناظرة بالنسبة للمحور البصري للجملة الإلكترونية البصرية. وتكون الوشائع محاطة بغلاف حديدي ذي شق حلقي يفصل بين نواتيْ القطبين. وتؤلف الوشائع لدى إمرار تيار كهربائي مستمر فيها مغنطيساً كهربائياً، وتزداد مقدرة العدسة على حرف الإلكترونات ـ ذات السرعة المعينة ـ بزيادة شدة التيار المار في الوشائع، كما تزداد بإنقاص المسافة بين النواتين.
تتألف أبسط عدسة مغنطيسية من سلك على هيئة عروة دائرية يمر فيها تيار مستمر، ويخضع الإلكترون المار من العروة لقوة مغنطيسية تسبب دورانه حول محور العروة مما يجعله ينحرف مقترباً من هذا المحور، ويتناسب مقدار الانحراف مع بعد الإلكترون عن المحور. فبهذه الطريقة تتجمع حزمة ضيقة من الإلكترونات صادرة من نقطة جسمية O في نقطة A هي خيال النقطة O (الشكل 7)، فالأمر شبيه بما يحدث للأشعة الضوئية في المنظار الفلكي أو المجهر. ويمكن أن يطبق في هذه الحالة قانون العدسة المقربة
حيث p: بعد الجسم عن العدسة، و: بعد خياله منها، وf: البعد المحرقي للعدسة، وقد تبين عمليـاً أن الإلكترونات الصادرة من الجسم O والتي تتبع مسارات شديدة الميل على محور الجملة لا تتجمع كلها في نقطة واحدة، أي يحدث زيغ حقيقي كما هو الأمر في العدسات الضوئية ولا يكون خيال النقطة نقطة بل بقعة صغيرة.
الإلكترون تاريخيا
أصل كلمة إلكترون يوناني (وهي تعني العنبر أو الكهرمان)، ويبدو أن الأيرلندي ج.ستوني G.Stoney هو أول من استعملها عام 1819. ومع أنه يصعب فصل تاريخ اكتشاف الإلكترون عن تاريخ الكهرباء المعروفة منذ العصور القديمة والتي أدت إلى تجارب متعددة في أواخر القرن الثامن عشر، يمكن القول إن تاريخ الإلكترون يبدأ باكتشاف وليام كروكس W.Crookes الأشعة المهبطية عام 1893. ويعود الفضل إلى ج. ج. طومسون J.J.Thomson في إثبات وجود الإلكترون وتقدير كتلته. ثم تتالت أعمال طُمْسون وهرتز Hertz ولورنتز Lorentz التي أدت إلى تعيين شحنة الإلكترون النوعية (نسبة شحنته e إلى كتلته m) البالغة 1.76 × 1110 كولون/كج. ثم قام ميليكان Millikan عام 1910 بإجراء تجربته الشهيرة التي تعتمد على جعل نقاط صغيرة جداً من الزيت، مشحونة بالكهرباء، تسقط بتأثير ثقلها بين مسريين electrodes أفقيين يمكن تغيير فرق الكمون بينهما، وتُستنتج كتلة نقطة الزيت من قياس سرعة سقوطها، وتُستنتج الشحنة التي تحملها بجعلها تتوازن بين المسريين باختيار فرق كمون مناسب بينهما. أما الشحنة العنصرية e فتُستنتج من دراسة عددٍ كبير من النقاط المختلفة كتلةً وشحنةً باعتبار أن شحنة أي نقطة ليست سوى مضاعفات صحيحة لهذه الشحنة العنصرية. ثم أتت تجارب رذرفورد Rutherford عام 1911 لتثبت وجود نواة مشحونة بشحنة كهربائية موجبة في مركز الذرة. وسرعان ما تبين أن الإلكترونات السالبة تتوزع حول هذه النواة لتكوِّن الذرة المعتدلة كهربائياً. ثم تبين بعد ذلك ضرورة افتراض أن الإلكترونات لا تخضع لقوانين الكهرمغنطيسية التقليدية وأنها لا تشع طاقة في أثناء حركتها على مداراتها حول النواة. وقد قام نيلز بور N.Bohr، بالاستناد إلى نظرية الكم quantum theory، بوضع نموذج الذرة المعروف باسمه. وتمَّ، بناءً على هذا النموذج، تفسير وظيفة الإلكترون في بنية الذرة وتوضيح منشأ الأطياف الضوئية التي تصدرها الذرات. وفي عام1925 بيّن ج. اولنبك G. Uhlenbeck وس. گودسميت S.Goudsmit أنه ينبغي أن يُعزى للإلكترون عزم اندفاع زاوي ذاتي سُمي سبين spin الإلكترون. وفي عام 1932 اكتشف أندرسون C.D. Anderson الإلكترون الموجب الذي كان ديراك Dirac قد تنبأ بوجوده في عام 1928 في دراسته النظرية المستندة إلى مبادئ ميكانيكا الكم ومبادئ النظرية النسبية.
وينص القانون الدوري أن الخواص الكيميائية للعناصر تكرر نفسها دوريا بشكل كبير وقد كان ذلك أساس الجدول الدوري للعناصر. وقد تم تفسير الجدول مبدئيا عن طريق الكتلة الذرية للعناصر. وعموما فإن الانحرافات التي كانت موجودة في الجدول الدوري تم تفسيرها لاحقا. في عام 1913 قام هنري موزلي بتقديم العدد الذري وقد فسر ذلك القانون الدوري عن طريق عدد البروتونات الموجودة في كل عنصر. وفي نفس العام قام نيلز بور بتوضيح أن الإلكترونات هي الأساس الفعلي للجدول. وفي عام 1916، قام گلبرت نيوتن لويس وإرڤنگ لانگموير بتوضيح الترابط الكيميائي للعناصر عن طريق تفاعل الإلكترونات .
| ” |
اعتدت أن أتعجب كيف أن الإلكترون سالب. سالب-موجب، تلك هي التماثلات البديعة في الفيزياء. ليس هناك سبب على الإطلاق لنفضل واحد على الآخر. ولكن لماذا الإلكترون سالب؟ لقد فكرت في هذا الأمر زمناً طويلاً، وأخيراً، كل ما أمكنني التفكير فيه كان "لقد ربح المعركة!". |
“ |
انظر أيضاً
- النموذج القياسي
- جسيم تحت ذري
- البروتون
- البوزيترون
- النيوترون
- التأثير الضوئي الإلكتروني
- البرق
- قائمة الجسيمات
- أشعة الكاثود
- الكهرباء
وصلات خارجية
المراجع
- ويكيبيديا الإنجليزية .
- ^ أ ب Mohr, Peter J. (2006-06-06). "CODATA recommended values of the fundamental physical constants". Reviews of Modern Physics. 80: 633–730. doi:10.1103/RevModPhys.80.633.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ The fractional version’s denominator is the inverse of the decimal value (along with its relative standard uncertainty of 5.0 × 10–8).
- ^ The electron’s charge is the سالب الشحنة الابتدائية، التي هي قيمة موجبة للپروتون.
الكتب المراجع
- Arabatzis, Theodore (2006). Representing Electrons: A Biographical Approach to Theoretical Entities. University of Chicago Press. ISBN 0226024210.
- Buchwald, Jed Z. (2001). Histories of the Electron: The Birth of Microphysics. MIT Press. ISBN 0262524244.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd edition ed.). Prentice Hall. ISBN 0-13-805326-X.
{{cite book}}:|edition=has extra text (help) - Leicester, Henry M. (1971). The Historical Background of Chemistry. Courier Dover Publications. ISBN 0486610535.
- Longair, Malcolm S. (1994). High Energy Astrophysics: Stars, the Galaxy and the Interstellar Medium. Cambridge University Press. ISBN 0521435846.
- Massimi, Michela (2005). Pauli's Exclusion Principle, The Origin and Validation of a Scientific Principle. Cambridge University Press. ISBN 0521839114.
- Numerous (1986). Soukhanov, Anne H. (ed.). Word Mysteries & Histories. Boston, MA: Houghton Mifflin Company. ISBN 0-395-40265-4.
- Numerous (1970). Guralnik, David B. (ed.). Webster's New World Dictionary. Englewood Cliffs, N. J.: Prentice-Hall, Inc.
- Raith, Wilhelm (2001). Constituents of Matter: Atoms, Molecules, Nuclei and Particles. CRC Press. ISBN 0849312027.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Reed, Bruce Cameron (2007). Quantum Mechanics. Jones & Bartlett Publishers. pp. 275–350. ISBN 0763744514.
- Rigden, John S. (2003). Hydrogen. Harvard University Press. pp. 59–86. ISBN 0674012526.
- Shipley, Joseph T. (1945). Dictionary of Word Origins. New York, N. Y.: Philosophical Library.
- Scerri, Eric R. (2007). The Periodic Table. Oxford University Press US. ISBN 0195305736.
- Schweber, Silvan S. (2005) [1962]. An Introduction to Relativistic Quantum Field Theory (2nd ed.). Dover Publications. ISBN 0-486-44228-4.
- Silk, Joseph (2000). The Big Bang: The Creation and Evolution of the Universe. Macmillan. ISBN 080507256X.
- Smirnov, Boris M. (2003). Physics of Atoms and Ions. Springer. ISBN 038795550X.
- Weinberg, Steven (2003). The Discovery of Subatomic Particles. Cambridge University Press. ISBN 052182351X.
- Zombeck, Martin V. (2007). Handbook of Space Astronomy and Astrophysics (Third edition ed.). Cambridge University Press. ISBN 0521782422.
{{cite book}}:|edition=has extra text (help)
وصلات خارجية
- The Discovery of the Electron from the American Institute of Physics History Center
- Particle Data Group
- Eric Weisstein's World of Physics: Electron
- Researchers Catch Motion of a Single Electron on Video