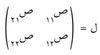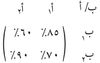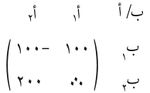نظرية الألعاب
في مفهومها الواسع يمكن فهم نظرية الألعاب على أنها أي معالجة علمية أي نظرية للعب ( المقصود باللعب هنا ليس اللهو فحسب بل هي تتعدى ذلك).
أما في مفهومها الأصلي فإن نظرية الألعاب هو مجال من مجالات إهتمام الرياضيات ولها أهمية كبيرة فيما يسمى بالبحوث العملياتية (Operation Research) و في العلوم الإقتصادية.
وتهتم نظرية الألعاب بدراسة إستراتجيات التصرف أو العمل في ظل نظام أو منظومة ذات قواعد معينة ( هذه القواعد تسمى اللعبة).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
مقدمة عامة
- هناك عدة دراسات (في الإعلامية مثلا) تهتم بنظرية الألعاب حيث يسعى الدارسون للبرهنة أنه في لعبة الشطرنج أو غيرها مثلا أن الذي يقوم بأول حركة يربح اللعبة دائما إذا إتبع الإستراتيجية الصحيحة.
أو أن الذي يقوم بالحركة الثانية يستطيع دائما أن يحقق تعادلا.
- إلى جانب دراسة الألعاب الذهنية تهتم نظرية الألعاب أيضا بالعلوم اللإقتصادية حيث ينظر للمعاملات التجارية على أساس أنها لعبة يحاول كل لاعب فيها تحقيق أكبر ربح ممكن.
- كما تهتم نظرية الألعاب بالعلوم الإنسانية كالسياسة و العلوم العسكرية كالإستراتيجية العسكرية ولكن في هذه المجالات تواجه النظرية بعض الصعوبات ذلك لأنها تسلم بأن اللاعبين يتصرفون بعقلانية كما أن كل جوانب الوضعية السياسية أو العسكرية يجب أن تؤخذ بعين الإعتبار عند وضع قواعد اللعبة.
البدايات
إن القالب العام لنظرية الألعاب تم وضعه على يد عالم الرياضيات الفرنسي Emile Borel إيمل بورل، الذي كتب أكثر من مقالة عن ألعاب الصدفة, ووضع منهجيات للعب, هذا ويعد أبو نظرية الألعاب الحقيقي هو عالم الرياضيات الهنغاري-الأمريكي John von Neuman جون فون نيومان, الذي أسس عبر سلسلة من المقالات أمتدت على مدى عشر سنوات (1920-1930)، الإطار الرياضي لأي تطوير على النظريات الفرعية. خلال الحرب العالمية الثانية, كانت معظم الخطط العسكرية ضمن مجال نقل الجنود وإيوائهم الدعم اللوجيستي ومجال الغواصات, و الدفاع الجوي, مرتبطة بشكل مباشر مع نظرية الألعاب. بعد ذلك تطورت نظرية الألعاب كثيراً في بيئة علم الاجتماع, ومع ذلك تعتبر نظرية الألعاب نتاج جوهري من علم الرياضيات.
تاريخ نظرية الألعاب
أسس علم نظرية الألعاب سنة 1944 على يد جون فون نيومان و أوسكار مورغن شتيرن و أشتهر عن طريق تأليفهما كتاب The Theory of Games and Economic Behavior. سنة 1994 تحصل كل من جون فوربوس ناش و رينارد سيلتين و جون هارسانيي على جائزة نوبل للإقتصاد و ذلك لأعمالهم في مجال تظرية الألعاب.
الخط الزمني
- قبل 1944: بعض الأعمال لكورنو بوريل و زيرميلو
- 1944:جون فون نيومان و أوسكار مورغن شتيرن يؤلفان كتاب The Theory of Games and Economic Behavior
- 1950 حتى 1960 تقريبا: إستعمال أول نماذج إقتصادية قائمة على نظرية الألعاب و القيام ببعض الدراسات في العلوم الإقتصادية التجريبية للتؤكد من صحة نتائج نظرية الألعاب.
- 1972:إقحام نظرية الألعاب في البيولوجيا التطورية (evolution biology) حيث ألف جون مينارد سميث كتاب Game Theory and the Evolution of Fighting
- 1994:جائزة نوبل لناش و زملائه لعملهم بعنوان: analysis of equilibria in the theory of non-games cooperative
مفاهيم و تقسيمات
- اللعبة: اللعبة موقف يجب على اللاعبين (على الأقل إثنين) فيه إتخاذ قرار.
مسلمات
- اللاعبون يتصرفون بعقلانية أي أنهم يحاولون جعل إحتمال وقوع عملية دفع ( أي تفوق أو ربح) أكثر إحتمالا.
- اللاعبون يتصرفون إستراتجيا: أي أنهم يحسبون أو يتكهنون حركة المنافس أو اللاعب الآخر و يدخلونها في حساباتهم.
تقسيم 1
يمكن تقسين الألعاب إلى:
- ألعاب ساكنة(static): حيث يجب على اللاعبين أن يقومو بإختيار إستراتجياتهم كلهم في نفس الوقت أي أن كلا منهم يتخذ قراره في نفس اللحظة و لا يستطيع أن يرى أولا ماذا فعل المنافس ثم يقرر.
- ألعاب دينامكية: يمكن للاعبين فيها أن يتخذو قراراتهم الواحد بعد الآخر.
تقسيم 2
- ألعاب بمعلومات كاملة: كل اللاعبين يعرفون نوايا (أي ما هي النتيجة التي يريد المنافس أن يصل إليها) منافسيهم و منافسوهم يعرفون ذلك وهم يعرفون أن منافسيهم يعلمون ذلك ...
- ألعاب بمعلومات منقوصة: واحد على الأقل من اللاعبين ليس له علم كامل بنوايا منافسيه. ،
تقسيم 3
- الألعاب التعاونية
- الألعاب غير التعاونية
أمثلة مشهورة
الحركة
في مفهوم نظرية الألعاب فإن الحركة هي التي تنقل اللعبة من مرحلة إلى أخرى, بدءاً من المرحلة الأولى وانتهاء بالمرحلة الأخيرة، والحركة قد تنتقل من لاعب إلى آخر بشكل محدد ومتتابع أو معاً، وإن قرار اتخاذ الحركة من الممكن أن يكون ناتجًا عن قرار شخصي أو بالصدفة, وفي الحالة الأخيرة يوجد غرض مثل حجر النرد أو دولاب الحظ، يحدد الحركة المعطاة وفقاً لآلية الاحتمالات.
الخرج/النصيب
الخرج, النصيب, النتيجة هو مصطلح لنظرية الألعاب يشير إلى ماذا حدث في نهاية اللعبة, في بعض الألعاب مثل الشطرنج أو الداما تكون النتيجة واضحة وبسيطة وذلك بتحديد الخاسر والرابح, في بعض ألعاب الرهان كالبوكر يكون النصيب هو النقود, وكمية النقود تحدد بعدد الرهانات التي وضعت أثناء اللعب.
الصيغة الشاملة والصيغة الطبيعية
يعتبر البحث في الفرق بين الصيغ الشاملة والصيغ الطبيعية من أهم دراسات نظرية الألعاب. نقول عن اللعبة بأنها في صيغتها الشاملة إذا تم تأليفها وفقاً لقواعد تحدد الحركات الممكنة في كل مرحلة, حيث تحدد على أي من اللاعبين عليه اللعب (الدور)، كما تحدد الاحتمالات الممكنة التي تنتج عن أي حركة للاعب أسندت إليه بالصدفة, كما تحدد هذه القواعد حجم النصيب-الخرج الممكن الناتج عن خوض اللعبة. كما أن الافتراض يقول أن كل لاعب لديه مجموعة من التفضيلات عند كل حركة بشكل توقع للخرج الممكن الذي إما سيضاعف نصيب اللاعب من النصيب أو يخسر. اللعبة في صيغتها الشاملة لا تحتوي فقط على لائحة من القوانين والقواعد التي تحكم تحرك كل لاعب, بل تحتوي أيضاً على مخطط من التفضيلات لكل لاعب، حيث الألعاب الجماعية الشائعة مثل (إكس أو) أو ألعاب الورق. إن أبسط الألعاب بصيغتها الشاملة تتضمن كمًّا هائلاً من المنهجيات والتخطيط لذلك طوّر الباحثون نمطًا جديدًا من الألعاب دعيت بالألعاب بصيغتها الطبيعية، حيث يمكن حساب النتائج بشكل كامل. وتكون اللعبة بصيغتها الطبيعية إذا أمكن وضع جميع النتائج أو الخرج لكل لاعب في حال اتخاذه أي قرار نابع عن استراتيجية ممكنة اتبعها، وهذا الشكل من الألعاب النظرية يمكن لعبه عن طريق أي مراقب حيادي لا يتأثر بقرارت يتخذها اللاعبون.
كمالية المعطيات
نقول عن اللعبة بأنها كاملة المعطيات إذا كانت جميع الحركات الممكنة معروفة لكل لاعب, الداما, و الشطرنج هما مثالان جيدان للعبة بمعطيات كاملة, البوكر تعتبر لعبة لا يمتلك فيها اللاعبون إلا قدراً محدودًا من المعطيات في بداية اللعبة.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
المنهج
المنهج أو الخطة هو قائمة اللاعب بالخيارات المثلى الممكنة في كل مرحلة من مراحل اللعبة, ويعتبر المنهج الذي يأخذ في الحسبان جميع الحركات الممكنة قبل اتخاذ القرار هو منهج لا يخيب, حيث لا مكان للأحداث المفاجئة بهكذا مناهج .
أنواع الألعاب
إن نظرية الألعاب تميز بين عدة أشكال من الألعاب ،وفقاً لعدد اللاعبين ولظروف اللعب نفسها.
لعبة الشخص الواحد/اللعب الفردية
السوليتير هي لعبة فردية, حيث لا وجود لتضارب مصالح حقيقية, لأن المصلحة الوحيدة هنا هي مصلحة اللاعب الفردي نفسه, وفي هذه اللعبة فإن الحظ أو الصدفة هو بنية اللعبة الأساسية وذلك اعتماداً على خلط الأوراق وعلى ما أمتلكه اللاعب من أوراق جيدة وزعت عليه عشوائياً. بالرغم من اهتمام نظرية الاحتمالات بالألعاب الفردية, إلا أنها لا تعتبر من المواضيع المحببة لدى نظرية الألعاب, حيث لا وجود لخصم يقوم باعتماد منهج مستقل ينافس به خيارات اللاعب الآخر.
لعبة الشخصين/الثنائية
يعتبر نمط الألعاب الثنائية من أكثر الأنماط انتشاراً، ويتضمن العديد من الألعاب المألوفة مثل الشطرنج, الداما, أو أي لعبة تعتمد على فريقين اثنين, والمعضلات الأكثر صعوبة هي التي تتضمن ن لاعب, كالألعاب الجماعية مثل: المونوبولي, البوكر, أو أي لعبة تتضمن لاعبين متعددين. إن الألعاب الثنائية قد تم تحليلها بشكل موسع في نظريات الألعاب ،والصعوبة الحقيقية في تمديد النتائج التي تم التوصل إليها لتشمل الألعاب بـ ن لاعب تكمن في توقع التفاعلات الممكنة بين مختلف اللاعبين, لأن في الألعاب الثنائية تكون جميع الخيارات والحركات الممكنة بالإضافة للنتائج تكون متوقعة, لكن عندما يكون هناك ثلاثة لاعبين أو أكثر, فإن احتمالات عشوائية معقدة من الخيارات والفرص تنشأ في ظل الظروف لتشكل تعاونا, او التحاما, أو اصطداما بين اللاعبين.
ألعاب صفرية المجموع ZeroSum
ذا كان مجموع الأرباح-الخرج في نهاية اللعبة هو صفر, فإن اللعبة صفرية المجموع, ويكون في هذه الألعاب كمية الربح أو احتماله مساوي تماماً لكمية الخسارة أو احتمالها, وهي المرادف لمصطلح تحليل التعادل الاقتصادي الذي يعبر عن الوصول إلى نقطة اللاربح ولا خسارة أو لا إنتاج ولا اهتلاك. سنة 1944 أظهر كل من فون نيومان, و أوسكار مورغنسنن Oskar Morgensten أن أي ن شخص لعبة صفرية المجموع من الممكن توسيعها إلى ن+1 شخص لعبة صفرية المجموع, وهكذا فإن ألعاب ن+1 شخص من الممكن تعميمها من الحالة الخاصة للألعاب الثنائية الصفرية المجموع. وإحدى أهم المسائل التي أثيرت في هذا المجال هي أن مبادىء التعظيم والتخفيض تطبق على جميع الألعاب الثنائية الصفرية المجموع, ويعرف هذا المصطلح بـ معضلة تخفيض-تعظيم, وقد تم اثباتها عن طريق نيومان سنة 1928, ونجح آخرون بالاثبات استناداً لطرق متعددة
نظرية المباراة
المباراة لعبة تقوم بين خصمين متنافسين (أ) و(ب) يفترض في رغبات أحدهما واهتماماته أن تعاكس رغبات الثاني واهتماماته، كما يفترض في ربح الأول أن يساوي خسارة الثاني، ويقال عن ذلك بإيجاز إنها لعبة ذات مجموع معدوم. ولقد اصطلح على أن تمثل هذه اللعبة بمصفوفة تدعى «مصفوفة اللعبة»، أو مصفوفة ربح اللاعب أ. (أو مصفوفة خسارة اللاعب ب). إن عدد أسطر هذه المصفوفة يساوي عدد خطط أحد اللاعبين، الذي يمكن أن يُدعى لاعب الأسطر، وعدد أعمدتها يساوي عدد خطط اللاعب الآخر الذي يدعى لاعب الأعمدة. أما عناصر هذه المصفوفة فهي أعداد حقيقية يمثل كل منها ص س ع ما يربحه اللاعب الأول أو ما يخسره (حسب إشارة العدد ص س ع) إذا قام باختيار الخطة الموافقة للسطر س ثم قام الآخر باختيار الخطة الموافقة للعمود «ع» أو العكس. فإذا كانت مجموعة خطط اللاعب أ هي: خ(أ)={أ1،أ2،...،أن} ومجموعة خطط خصمه ب هي: خ(ب)= {ب1،ب2،...بم} وكان أ هو لاعب الأعمدة وكان ب هو لاعب الأسطر أمكن كتابة مصفوفة اللعبة على النحو:
وهكذا فإن كل لعبة تمثل بمصفوفة، ويمكن النظر إلى أي مصفوفة على أنها تمثل لعبة من هذا النمط. وعلى سبيل المثال فان المصفوفة:
تمثل لعبة فيها ن=4، م=3. ولمعرفة كيف تجري اللعبة، يفترض أن أ هو الذي بدأ باللعب ساعياً إلى الحصول على أعلى ربح ممكن، تجدر ملاحظة ما يلي: لو اختار أ العمود الأول لاختار ب السطر الأول ولربح أ خمس ليرات (مثلاً) ولو اختار أ العمود الثاني لاختار ب السطر الثالث ولخسر أ 12 ليرة، أما لو اختار أ العمود الثالث لاختار ب السطر الثاني ولخسر أ ست ليرات، وأخيراً لو اختار أ العمود الرابع لاختار ب السطر الثاني ولربح أ ليرة واحدة. ومن هذا يتضح أن أفضل ما يفعله أ هو أن يلعب وفق الخطة الموافقة للعمود الأول، أو كما يقال عادة: إن أحسن ما يفعله أ هو اختيار العمود الأول، وعندئذ يضمن ربحاً قدره خمس ليرات على الأقل مهما كانت الخطة التي سيجابهه بها خصمه. وما على أ كي يصل إلى هذا القرار سوى أن يستبدل بكل عمود أصغر عدد فيه فيحصل على الأعداد 5،-12،-6، 1، ثم يختار أكبرها ص س1 ع1 وهو العدد 5 ثم يختار العمود الذي يبلغه هذا الهدف ع1=1. أما لو اضطر ب إلى بدء اللعب فهو سيسعى إلى الوصول إلى أقل خسارة ممكنة، وعليه في سبيل ذلك أن يستبدل بكل سطر أكبر عدد فيه فيحصل على الأعداد 12،11،9 ثم يختار أصغرها ص س2 ع2 وهو العدد 9 ثم يختار السطر الذي يبلغه هذا الهدف س2=3. مما سبق ينتج أنه إذا بدأ أ اللعبة فان أعلى ربح يحصل عليه في جولة اللعب هذه هو: 5=صس1ع1=نع1 ³ ع ³ ن (نص1 ³ س ³ م(صس ع)) أما إذا بدأ ب اللعبة فإن أقل خسارة تصيبه في هذه الجولة هي:
9=صس2ع2=نص1 ³ س ³ م (نع1 ³ ع ³ ن(صس ع))
ويبرهن في المصفوفة (1) أن ص س1ع1 ³ ص س2ع2 دائماً وهنا يلاحظ أن ص س1ع1< ص س2ع2 في المصفوفة (2)، أما في المصفوفة
فإن ص س1ع1= ص س2ع2=7، وقد وضعت هذه القيمة ضمن مربع صغير. تدعى القيمة 7 قيمة اللعبة ويدعى المربع الذي تشغله هذه القيمة في مصفوفة اللعبة نقطة استقرار اللعبة أو نقطة توازنها. وهنا يتضح أنه لو بدأ أي من اللاعبين اللعب فسيختار السطر (العمود) الذي يوصله إلى نقطة التوازن. ويقال هنا إن اللاعبين كليهما يسعيان إلى الاستقرار فيها، ويحاول كل خصم إخراج خصمه منها مستخدماً الحيلة والحزر. وتبرز صعوبة الاختيار لدى الخصمين عندما تكون المعلومات المتوافرة لدى كل منهما عن الآخر ناقصة. ويلاحظ أنه إذا كان لمصفوفة اللعبة نقطة توازن وحيدة فإن شوطاً واحداً (مرحلة واحدة) يمكن أن ينهيها. وتكرار الشوط (إعادته) يقود إلى النتيجة نفسها، وهي ربح لـِ أ قيمته تساوي قيمة اللعبة، وخسارة لـ ِ ب تساوي نظير قيمة اللعبة. أما إذا لم يكن لمصفوفة اللعب نقطة توازن وحيدة (أي ليس لها أي نقطة توازن أو لها أكثر من نقطة)، وإذا فُرض أن أ يريد أن يزيد ربحه الذي تضمنه له طريقة اللعب السابق ذكرها، وأن ب يريد كذلك أن يخفف من خسارته، وأن اللعبة تتضمن أشواطاً عدة وأن كل لاعب يتصرف كما يحلو له معتمداً على الحظ والمصادفة إلى جانب الحيلة والحيطة والحزر فيختار أ مثلاً العمود د باحتمال قيمته ق د ويختار ب السطر ر باحتمال قيمته ك ر، عندئذ يدعى
![]() استراتيجية لـِ أ ويدعى ك=[ك1،...كم] إستراتيجية لـِ ب، ويكون احتمال أن يربح أ المقدار صرد هو ك ر× ق د (بحسب قواعد الاحتمال). تدعى الدالة (التابع):
استراتيجية لـِ أ ويدعى ك=[ك1،...كم] إستراتيجية لـِ ب، ويكون احتمال أن يربح أ المقدار صرد هو ك ر× ق د (بحسب قواعد الاحتمال). تدعى الدالة (التابع):
معدل ربح اللاعب أ، أو معدل خسارة اللاعب ب. وتؤكد نظرية فون نيومان Von Neuman أن ثمة إستراتيجية ق* لـِ أ، وأخرى ك* لـ ِ ب، تدعى كل منها إستراتيجية مثلى، بحيث يتحقق ما يلي: ت(ق،ك*) ³ ت(ق*،ك*) ³ ت(ق*،ك)
أياً كانت الاستراتيجيتان ق، ك وتدعى القيمة ت(ق*، ك*)=هـ قيمة اللعبة. ويقال عن استراتيجية ق للاعب أ إنها "رائية" صرفة إذا كان
ق=[\، \ ،...،1،...، \]=[ق1، ق2،...،قر،...،قن]
أي إذا كان ق ر=1، وكان ق رَ=\ عندما يكون ر¹ رَ. كذلك يقال عن إستراتيجية ك للاعب ب إنها «دالية» صرفة إذا كان ك د=1، ك دَ=\ عندما يكون دَ¹ د. أما إذا كان\ >ق> 1 فإنه يقال: إن ق استراتيجية غير صرفة أو أنها استراتيجية مزيجة. ويبرهن أنه إذا كانت مصفوفة اللعبة هي
وإذا لم يكن لهذه المصفوفة أي نقطة توازن فإن الإستراتيجية المثلى ق* للاعب أ هي:
وإن الإستراتيجية المثلى ك* للاعب ب هي:
وتكون قيمة اللعبة هي:
فإذا أرادت وزارة الصحة، مثلاً، أن تقوم بتلقيح مواطنيها لوقايتهم من فيروس معين، وإذا فرض أن لهذا الفيروس سلالتين، وأنه لا يُعرف شيء عن النسب التي تظهر فيها هاتان السلالتان في الفيروس. وإذا فُرض أنه تم الوصول إلى تلقيحين بتأثيرين مختلفين على السلالتين، وأن التلقيح الأول فعّال بنسبة 85% للوقاية من السلالة الأولى و70% للوقاية من السلالة الثانية، وأن التلقيح الثاني فعّال بنسبة 60% للوقاية من السلالة الأولى و90% للوقاية من السلالة الثانية، فما هي سياسة التلقيح المثلى التي ينبغي على وزارة الصحة الأخذ بها. تمثل هذه المسألة مباراة، اللاعب أ فيها هو وزارة الصحة واللاعب ب هو الفيروس. يرغب اللاعب أ في الحصول على أفضل ربح (أعلى نسبة من المواطنين الممنعين للوقاية من الفيروس) ويرغب اللاعب ب أن يخفف من هذا الربح إلى أقل ما يمكن. إن مصفوفة اللعب هي:
وليس لهذه المصفوفة أي نقطة توازن. لذا فإن الاستراتيجية المثلى ق* للاعب أ هي:
وأن الاستراتيجية المثلى للاعب ب هي:
وتكون قمة اللعبة هي
وهنا نلاحظ أن الاستراتيجية المثلى لوزارة الصحة هي أن تلقح ثلثي المواطنين باللقاح الأول وأن تلقح الثلث الباقي باللقاح الثاني. عندئذ يحصل 76.7% من المواطنين على مناعة للوقاية من الفيروس بغض النظر عن توزع السلالتين فيه. ومن جهة أخرى فإن الفيروس بنسبة من السلالة الأولى و من السلالة الثانية بجعل نسبة المواطنين المقاومين له لا تتجاوز 76.7% بغض النظر عن استراتيجية التلقيح التي تبنتها وزارة الصحة.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
نظرية الحيل
يستخدم كل لاعب في المباراة الحيلة والحذر عندما لا تكون لديه معلومات كافية عن خطط خصمه، ويسعى للتستر على نواياه، ولكشف نوايا خصمه آملاً بالفوز. وهنا يشار إلى أنه يجب أن لا تستخدم الحيلة نفسها عدة مرات إذ تصبح خطته مكشوفة للخصم، ويعود ضررها على من استخدمها. كذلك يتعين على اللاعب أن يغير خطته أو خطط لعبه تبعاً لردود فعل الخصم، وعليه أن يراوغ في اختيار خطته وفق ما يراه مناسباً. ومع ذلك قد يصعب عليه الفوز. وقد أورد أوسكار مورغنشترن Oscar Morgenstern مثالاً لاختبارات عشوائية لمواقف عشوائية وذلك باستخدامه مغامرة شرلوك هولمز Sherlock Holmes التالية: يهرب هولمز من شخص يتعقبه ليقتله هو موريارتي Moriarty، فيأخذ الأول قطاراً من لندن إلى مدينة "دوفر" على الساحل المقابل لفرنسة، ويمر القطار، في طريقه بمدينة كانتربري، ويلمح هولمز، لسوء حظه، حين صعوده إلى القطار أن متعقبه يسافر معه في الرحلة ذاتها فلو نزلا من القطار معاً لعرض نفسه للهلاك. أما لو نزل هولمز في دوفر ونزل الآخر في كانتربري، فإن هولمز ينجو، ويستقل بعدئذ باخرة إلى فرنسة. لكن إذا حدث أن نزل هو في كانتربري ونزل خصمه في دوفر فإن هولمز سيخفق في الهرب. وينتج من هذا صعوبة الاختيار لدى الخصمين لنقص المعلومات المتوافرة لدى كل منهما، ولذا فإن خطة كل منهما دفاعية ويرتبط حلها بالمصادفة والحظ وواضح كذلك أن كلاً منهما يترقب صدور أقل هفوة من صاحبه ليفاجئه بخطة هجومية قد تحقق له ما يريد. ويمكن أن تعطى هذه اللعبة الصيغة الرياضية التالية، وذلك بإدخال احتمال الخيارات الممكنة لكل خصم. فلو فرضنا أن احتمال نزول هولمز في دوفر هو ق واحتمال نزول خصمه في كانتربري هو ك فيكون، وفقاً لقواعد الاحتمال، احتمال نجاح هولمز في الهرب يساوي ق×ك واحتمال إخفاقه في الهرب دون أن يتعرض للقتل هو (1- ق) (1- ك) واحتمال تعرضه للقتل هو
(1- ق) ك+ ق (1- ك) = ق + ك -2ق ك.
ولكن هذه الاحتمالات غير معروفة بدقة، بل هي ظنّية. فلو عرف هولمز نفسه احتمال نزول خصمه في كانتربري لما كان اختياره عشوائياً. وهنا يتصرف كل لاعب تبعاً لأفكاره التي يحملها عن خصمه ويلجأ إلى التخمين والتقدير. فلو قدر هولمز أن ك صغيرة ربما اختار النزول في كانتربري وآثر الاخفاق مع السلامة على ما سوى ذلك، أما لو قدر هولمز استناداً إلى معلومات وصلت إليه بطريقة ما أنه إذا نزل في كانتربري، فالإخفاق محقق ومؤكد له. وإذا نزل في دوفر فقد ينجح باحتمال قدره 90%، أو يفضل (وهذا راجع لتقديراته) أن يعرض نفسه للموت بنسبة 10% مقابل تسع مرات نجاح في العشرة.
تطبيقات نظرية الألعاب في الاقتصاد
ظهرت أولى التطبيقات الاقتصادية لنظرية الألعاب عام 1944 في كتاب عنوانه: نظرية الألعاب والسلوك الاقتصادي ألّفه مورغنشترن O.Horgenstern، وفون نيومان J.Von Neuman. وفي الواقع فإن مبدأ تطبيق نظرية الألعاب في الاقتصاد بسيط نسبياً. فإذا أخذنا بالنظرية التقليدية في الاقتصاد فإن كل اقتصادي يسعى إلى بلوغ النهاية العظمى أو النهاية الصغرى لتابع يدعى تابعاً اقتصادياً أو تابع الربح أو تابع الكلفة أو ما ماثل ذلك. فمدير أي مشروع مثلاً يسعى للوصول إلى أكبر ربح لمشروعه. فينظر في تابع الربح ويسعى إلى بلوغ نهايته العظمى، في حين يسعى أي مستهلك لبلوغ النهاية الصغرى لتابع الكلفة. وتظهر أهمية نظرية الألعاب عند دراسة المنافسات بين المؤسسات الاقتصادية التي يحاول كل منها اختيار القرار الأمثل. ويمكن لتوضيح الفكرة إيراد المثال التالي: تتنافس مؤسستان اقتصاديتان على اقتسام جمهور المستهلكين في سوق محلية فتقوم كل منهما بين الحين والآخر بحملة دعاية عن طريق الصحف أو بالملصقات الجدارية. فإذا افترض أن مدير أولى المؤسستين توصل إلى ما يلي: إذا قام بحملة الدعاية في الصحف (الاختيار أ1) فإنه يحقق ربحاً لمؤسسته قدره مئة ألف ليرة فيما لو اختار منافسه الدعاية في الصحف (الاختيار ب1)، ولكن ربحه سيكون صفراً لو اختار منافسه الدعاية بالملصقات الجدارية (الاختيار أ2).أما إذا قام بحملة الدعاية بالملصقات الجدارية (الاختيار ) فانه يخسر مئة ألف ليرة سورية فيما لو اختار منافسه الدعاية في الصحف (الاختيار ب1)، ولكن ربحه سيكون مئتي ألف ليرة لو اختار منافسه الدعاية بالملصقات الجدارية (الاختيار ب2). فما هو القرار الأمثل لكل منهما:
يمكن تمثيل هذه المنافسة بمصفوفة ربح المؤسسة الأولى (اللاعب الأول أ)
واستناداً إلى ما سبق تكون قيمة اللعبة هـ =50 ألفاً، وتكون الاستراتيجية المثلى لـِ أ هي
وتعني هذه النتيجة أن القرار الأمثل للمؤسسة الأولى هو أن تصرف ثلاثة أرباع المبلغ المخصص لحملة الدعاية للدعاية بالصحف والربع الباقي للدعاية بالملصقات. عندئذ تضمن ربحاً لا يقل عن خمسين ألفاً مهما كانت الخطة التي ستتبناها المؤسسة الثانية (اللاعب ب). أما الاستراتيجية المثلى لـِ ب
فهي والقرار الأمثل لها هو أن تصرف نصف المبلغ للدعاية في الصحف، والنصف الآخر للدعاية بالملصقات الجدارية. عندئذ لن تتجاوز خسارة هذه المؤسسة خمسين ألفاً مهما كانت الخطة التي ستنتهجها المؤسسة الأولى والدالة الاقتصادية التي تمثل ربح أ هي:
ت(ق،ك)=ت(ق1،ق2، ك1،ك2)=تا(س،ع)=400س ع -300 ع-200س+200
بفرض أن ق1=س، ق2=1-س، ك1=ع، ك2=1-ع.
والنقطة الحرجة لهذا التابع هي
مصادر وقراءات إضافية
مواقع إلكترونية
- [1]
- [2]
- Paul Walker: History of Game Theory Page.
- Game Theory 101: Introductory game theory video lectures.
- David Levine: Game Theory. Papers, Lecture Notes and much more stuff.
- Alvin Roth: Game Theory and Experimental Economics page - Comprehensive list of links to game theory information on the Web
- Adam Kalai: Game Theory and Computer Science - Lecture notes on Game Theory and Computer Science
- Mike Shor: Game Theory .net - Lecture notes, interactive illustrations and other information.
- Jim Ratliff's Graduate Course in Game Theory (lecture notes).
- Valentin Robu's software tool for simulation of bilateral negotiation (bargaining)
- Don Ross: Review Of Game Theory in the Stanford Encyclopedia of Philosophy.
- Bruno Verbeek and Christopher Morris: Game Theory and Ethics
- Chris Yiu's Game Theory Lounge
- Elmer G. Wiens: Game Theory - Introduction, worked examples, play online two-person zero-sum games.
- Marek M. Kaminski: Game Theory and Politics - syllabuses and lecture notes for game theory and political science.
- Web sites on game theory and social interactions
- Kesten Green's Conflict Forecasting - See Papers for evidence on the accuracy of forecasts from game theory and other methods.
- McKelvey, Richard D., McLennan, Andrew M., and Turocy, Theodore L. (2007) Gambit: Software Tools for Game Theory.
- Benjamin Polak: Open Course on Game Theory at Yale videos of the course
- Benjamin Moritz, Bernhard Könsgen, Danny Bures, Ronni Wiersch, (2007) Spieltheorie-Software.de: An application for Game Theory implemented in JAVA.